Section xiii.
Of the attractive forces of bodies which are not of a sphaerical figure.
Proposition lxxxv. Theorem xlii.
If a body be attracted by another, and its attraction be vastly stronger when it is contiguous to the attracting body than when they are separated from one another by a very small interval; the forces of the particles of the attracting body decrease, in the recess of the body attracted, in more than a duplicate ratio of the distance of the particles.
For if the forces decrease in a duplicate ratio of the distances from the particles, the attraction towards a sphaerical body being (by Prop. LXXIV) reciprocally as the square of the distance of the attracted body from the centre of the sphere, will not be sensibly increased by the contact, and it will be still less increased by it, if the attraction, in the recess of the body attracted, decreases in a still less proportion. The proposition, therefore, is evident concerning attractive spheres. And the case is the same of concave sphaerical orbs attracting external bodies. And much more does it appear in orbs that attract bodies placed within them, because there the attractions diffused through the cavities of those orbs are (by Prop. LXX) destroyed by contrary attractions, and therefore have no effect even in the place of contact. Now if from these spheres and sphaerical orbs we take away any parts remote from the place of contact, and add new parts any where at pleasure, we may change the figures of the attractive bodies at pleasure; but the parts added or taken away, being remote from the place of contact, will cause no remarkable excess of the attraction arising from the contact of the two bodies. Therefore the proposition holds good in bodies of all figures. Q.E.D.
Proposition lxxxvi. Theorem xliii.
If the forces of the particles of which an attractive body is composed decrease, in the recess of the attractive body, in a triplicate or more than a triplicate ratio of the distance from the particles, the attraction will be vastly stronger in the point of contact than when the attracting and attracted bodies are separated from each other, though by never so small an interval.
For that the attraction is infinitely increased when the attracted corpuscle comes to touch an attracting sphere of this kind, appears, by the solution of Problem XLI, exhibited in the second and third Examples. The same will also appear (by comparing those Examples and Theorem XLI together) of attractions of bodies made towards concavo-convex orbs, whether the attracted bodies be placed without the orbs, or in the cavities within them. And by adding to or taking from those spheres and orbs any attractive matter any where without the place of contact, so that the attractive bodies may receive any assigned figure, the Proposition will hold good of all bodies universally. Q.E.D.
Proposition lxxxvii. Theorem xliv.
If two bodies similar to each other, and consisting of matter equally attractive, attract separately two corpuscles proportional to those bodies, and in a like situation to them, the accelerative attractions of the corpuscles towards the entire bodies will be as the accelerative attractions of the corpuscles towards particles of the bodies proportional to the wholes, and alike situated in them.
For if the bodies are divided into particles proportional to the wholes, and alike situated in them, it will be, as the attraction towards any particle of one of the bodies to the attraction towards the correspondent particle in the other body, so are the attractions towards the several particles of the first body, to the attractions towards the several correspondent particles of the other body; and, by composition, so is the attraction towards the first whole body to the attraction towards the second whole body. Q.E.D.
Cor. 1 . Therefore if, as the distances of
the corpuscles attracted increase, the attractive forces of the
particles decrease in the ratio of any power of the distances, the
accelerative attractions towards the whole bodies will be as the
bodies directly, and those powers of the distances inversely. As if
the forces of the particles decrease in a duplicate ratio of the
distances from the corpuscles attracted, and the bodies are as A³ and
B³, and therefore both the cubic sides of the bodies, and the distance
of the attracted corpuscles from the bodies, are as A and B; the
accelerative attractions towards the bodies will be as
A3
A2 and
B3
B2, that is, as A and B the
cubic sides of those bodies. If the forces of the particles decrease
in a triplicate ratio of the distances from the attracted corpuscles,
the accelerative attractions towards the whole bodies will be as
A3
A3 and
B3
B3, that is, equal. If the
forces decrease in a quadruplicate ratio, the attractions towards the
bodies will be as A3
A4 and
B3
B4, that is, reciprocally as
the cubic sides A and B. And so in other cases.
Cor. 2. Hence, on the other hand, from the forces with which like bodies attract corpuscles similarly situated, may be collected the ratio of the decrease of the attractive forces of the particles as the attracted corpuscle recedes from them; if so be that decrease is directly or inversely in any ratio of the distances.
Proposition lxxxviii. Theorem xlv.
If the attractive forces of the equal particles of any body be as the distance of the places from the particles, the force of the whole body will tend to its centre of gravity; and will be the same with the force of a globe, consisting of similar and equal matter, and having its centre in the centre of gravity.
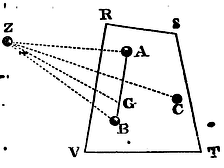
Let the particles A, B, of the body RSTV attract any corpuscle Z with forces which, supposing the particles to be equal between themselves, are as the distances AZ, BZ; but, if they are supposed unequal, are as those particles and their distances AZ, BZ, conjunctly, or (if I may so speak) as those particles drawn into their distances AZ, BZ respectively. And let those forces be expressed by the contents under A x AZ, and B x BZ. Join AB, and let it be cut in G, so that AG may be to BG as the particle B to the particle A; and G will be the common centre of gravity of the particles A and B. The force A x AZ will (by Cor. 2, of the Laws) be resolved into the forces A x GZ and A x AG; and the force B x BZ into the forces B x GZ and B x BG. Now the forces A x AG and B x BG, because A is proportional to B, and BG to AG, are equal, and therefore having contrary directions destroy one another. There remain then the forces A x GZ and B x GZ. These tend from Z towards the centre G, and compose the force (A + B) x GZ; that is, the same force as if the attractive particles A and B were placed in their common centre of gravity G, composing there a little globe.
By the same reasoning, if there be added a third particle C, and the force of it be compounded with the force (A + B) x GZ tending to the centre G, the force thence arising will tend to the common centre of gravity of that globe in G and of the particle C; that is, to the common centre of gravity of the three particles A, B, C; and will be the same as if that globe and the particle C were placed in that common centre composing a greater globe there; and so we may go on in infinitum. Therefore the whole force of all the particles of any body whatever RSTV is the same as if that body, without removing its centre of gravity, were to put on the form of a globe. Q.E.D.
Cor. Hence the motion of the attracted body Z will be the same as if the attracting body RSTV were sphaerical; and therefore if that attracting body be either at rest, or proceed uniformly in a right line, the body attracted will move in an ellipsis having its centre in the centre of gravity of the attracting body.
Proposition lxxxix. Theorem xlvi.
If there be several bodies consisting of equal particles whose forces are as the distances of the places from each, the force compounded of all the forces by which any corpuscle is attracted will tend to the common centre of gravity of the attracting bodies; and will be the same as if those attracting bodies, preserving their common centre of gravity, should unite there, and be formed into a globe.
This is demonstrated after the same manner as the foregoing Proposition.
Cor. Therefore the motion of the attracted body will be the same as if the attracting bodies, preserving their common centre of gravity, should unite there, and be formed into a globe. And, therefore, if the common centre of gravity of the attracting bodies be either at rest, or proceed uniformly in a right line, the attracted body will move in an ellipsis having its centre in the common centre of gravity of the attracting bodies.
Proposition xc. Problem xliv.
If to the several points of any circle there tend equal centripetal forces, increasing or decreasing in any ratio of the distances; it is required to find the force with which a corpuscle is attracted, that is, situate any where in a right line which stands at right angles to the plant of the circle at its centre.
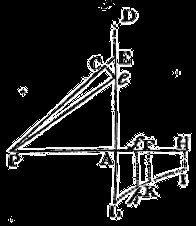
Suppose a circle to be described about the centre A with any interval AD in a plane to which the right line AP is perpendicular; and let it be required to find the force with which a corpuscle P is attracted towards the same. From any point E of the circle, to the attracted corpuscle P, let there be drawn the right line PE. In the right line PA take PF equal to PE, and make a perpendicular FK, erected at F, to be as the force with which the point E attracts the corpuscle P. And let the curve line IKL be the locus of the point K. Let that curve meet the plane of the circle in L. In PA take PH equal to PD, and erect the perpendicular HI meeting that curve in I; and the attraction of the corpuscle P towards the circle will be as the area AHIL drawn into the altitude AP. Q.E.I.
For let there be taken in AE a very small line Ee. Join Pe,
and in PE, PA take PC, Pf equal to Pe. And because
the force, with which any point E of the annulus described about the
centre A with the interval AE in the aforesaid plane attracts to
itself the body P, is supposed to be as FK; and, therefore, the force
with which that point attracts the body P towards A is as
AP x FK
PE; and the force with which the whole
annulus attracts the body P towards A is as the annulus and
AP x FK
PE conjunctly; and that annulus also is
as the rectangle under the radius AE and the breadth Ee, and
this rectangle (because PE and AE, Ee and CE are
proportional) is equal to the rectangle PE x CE or PE x Ff;
the force with which that annulus attracts the body P towards A will
be as PE x Ff and AP x
FK
PE conjunctly; that is, as the content
under Ff x FK x AP, or as the area FKkf drawn into
AP. And therefore the sum of the forces with which all the annuli, in
the circle described about the centre A with the interval AD, attract
the body P towards A, is as the whole area AHIKL drawn into AP.
Q.E.D.
Cor. 1. Hence if the forces of the points
decrease in the duplicate ratio of the
distances, that is, if FK be as
1
PF2 and therefore the
area AHIKL as 1
PA − 1
PH; the attraction of the
corpuscle P towards the circle will be as 1 −
PA
PH; that is, as
AH
PH.
Cor. 2. And universally if the forces of the
points at the distances D be reciprocally as any power Dn
of the distances; that is, if FK be as 1
Dn and therefore the area
AHIKL as 1
PAn-1 −
1
PHn-1; the
attraction of the corpuscle P towards the circle will be as
1
PAn-2 −
1
PHn-1.
Cor. 3. And if the diameter of the circle be
increased in infinitum, and the number n be
greater than unity; the attraction of the corpuscle P towards the
whole infinite plane will be reciprocally as PAn-2, because
the other term PA
PAn-1 vanishes.
Proposition xci. Problem xlv.
To find the attraction of a corpuscle situate in the axis of a round solid, to whose several points there tend equal centripetal forces decreasing in any ratio of the distances whatsoever.
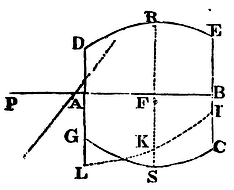
Let the corpuscle P, situate in the axis AB of the solid DECG, be attracted towards that solid. Let the solid be cut by any circle as RFS, perpendicular to the axis: and in its semi-diameter FS, in any plane PALKB passing through the axis, let there be taken (by Prop. XC) the length FK proportional to the force with which the corpuscle P is attracted towards that circle. Let the locus of the point K be the curve line LKI, meeting the planes of the outermost circles AL and BI in L and I; and the attraction of the corpuscle P towards the solid will be as the area LABI. Q.E.I.
Cor. 1. Hence if the solid be a cylinder
described by the parallelogram ADEB revolved about the axis AB, and
the centripetal forces tending to the several points be reciprocally
as the squares of the distances from the points; the attraction of the
corpuscle P towards this cylinder will be as AB − PE + PD. For the
ordinate FK (by Cor. 1, Prop. XC) will be as 1 −
PF
PR. The part 1 of this quantity, drawn
into the length AB, describes
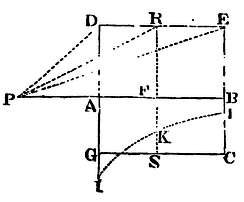 the area 1 x AB; and the other part PF
the area 1 x AB; and the other part PF
PR, drawn into the length PB describes the area 1
into (PE − AD) (as may be easily shewn from the quadrature of
the curve LKI); and, in like manner, the same part drawn into the
length PA describes the area 1 into (PD − AD),
and drawn into AB, the difference of PB and PA, describes 1
into (PE − PD), the difference of the areas. From the first
content 1 x AB take away the last content 1 into
(PE − PD), and there will remain the area LABI equal to
1 into (AB − PE + PD). Therefore the force,
being proportional to this area, is as AB − PE +
PD.
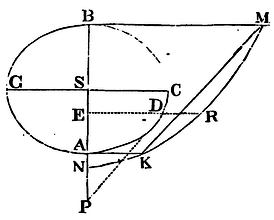
Cor. 2. Hence also is known the force by
which a spheroid AGBC attracts any body P situate externally in its
axis AB. Let NKRM be a conic section whose ordinate ER perpendicular
to PE may be always equal to the length of the line PD, continually
drawn to the point D in which that ordinate cuts the spheroid. From
the vertices A, B, of the spheriod, let there be erected to its axis
AB the perpendiculars AK, BM, respectively equal to AP, BP, and
therefore meeting the conic section in K and M; and join KM cutting
off from it the segment KMRK. Let S be the centre of the spheroid, and
SC its greatest semi-diameter; and the force with which the spheroid
attracts the body P will be to the force with which a sphere described
with the diameter AB attracts the same body as
AS x CS2 − PS x KMRK
PS2 + CS2 − AS2
is to AS3
3PS2. And by a
calculation founded on the same principles may be found the forces of
the segments of the spheroid.
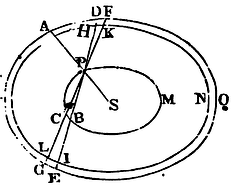
Cor. 3. If the corpuscle be placed within the spheroid and in its axis, the attraction will be as its distance from the centre. This may be easily collected from the following reasoning, whether the particle be in the axis or in any other given diameter. Let AGOF be an attracting spheroid, S its centre, and P the body attracted. Through the body P let there be drawn the semi-diameter SPA, and two right lines DE, FG meeting the spheroid in D and E, F and G; and let PCM, HLN be the superficies of two interior spheroids similar and concentrical to the exterior, the first of which passes through the body P, and cuts the right lines DE, FG in B and C; and the latter cuts the same right lines in H and I, K and L. Let the spheroids have all one common axis, and the parts of the right lines intercepted on both sides DP and BE, FP and CG, DH and IE, FK and LG, will be mutually equal; because the right lines DE, PB, and HI, are bisected in the same point, as are also the right lines FG, PC, and KL. Conceive now DPF, EPG to represent opposite cones described with the infinitely small vertical angles DPF, EPG, and the lines DH, EI to be infinitely small also. Then the particles of the cones DHKF, GLIE, cut off by the spheroidical superficies, by reason of the equality of the lines DH and EI, will be to one another as the squares of the distances from the body P, and will therefore attract that corpuscle equally. And by a like reasoning if the spaces DPF, EGCB be divided into particles by the superficies of innumerable similar spheroids concentric to the former and having one common axis, all these particles will equally attract on both sides the body P towards contrary parts. Therefore the forces of the cone DPF, and of the conic segment EGCB, are equal, and by their contrariety destroy each other. And the case is the same of the forces of all the matter that lies without the interior spheroid PCBM. Therefore the body P is attracted by the interior spheroid PCBM alone, and therefore (by Cor. 3, Prop. LXXII) its attraction is to the force with which the body A is attracted by the whole spheroid AGOD as the distance PS to the distance AS. Q.E.D.
Proposition xcii. Problem xlvi.
An attracting body being given, it is required to find the ratio of the decrease of the centripetal forces tending to its several points.
The body given must be formed into a sphere, a cylinder, or some regular figure, whose law of attraction answering to any ratio of decrease may be found by Prop. LXXX, LXXXI, and XCI. Then, by experiments, the force of the attractions must be found at several distances, and the law of attraction towards the whole, made known by that means, will give the ratio of the decrease of the forces of the several parts; which was to be found.
Proposition xciii. Theorem xlvii.
If a solid be plane on one side, and infinitely extended on all other sides, and consist of equal particles equally attractive, whose forces decrease, in the recess from the solid, in the ratio of any power greater than the square of the distances; and a corpuscle placed towards either part of the plane is attracted by the force of the whole solid; I say that the attractive force of the whole solid, in the recess from its plane superficies, will decrease in the ratio of a power whose side is the distance of the corpuscle from the plane, and its index less by 3 than the index of the power of the distances.
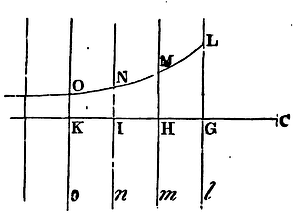
Case 1. Let LGl be the plane by which the solid is terminated. Let the solid lie on that hand of the plane that is towards I, and let it be resolved into innumerable planes mHM, nIN, oKO, &c., parallel to GL. And first let the attracted body C be placed without the solid. Let there be drawn CGHI perpendicular to those innumerable planes, and let the attractive forces of the points of the solid decrease in the ratio of a power of the distances whose index is the number n not less than 3. Therefore (by Cor. 3, Prop. XC) the force with which any plane mHM attracts the point C is reciprocally as CHn-2. In the plane mHM take the length HM reciprocally proportional to CHn-2, and that force will be as HM. In like manner in the several planes lGL, nIN, oKO, &c., take the lengths GL, IN, KO, &c., reciprocally proportional to CGn-2, CIn-2, CKn-2, &c., and the forces of those planes will be as the lengths so taken, and therefore the sum of the forces as the sum of the lengths, that is, the force of the whole solid as the area GLOK produced infinitely towards OK. But that area (by the known methods of quadratures) is reciprocally as CGn-3, and therefore the force of the whole solid is reciprocally as CGn-3. Q.E.D.
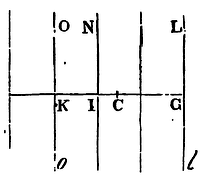
Case 2. Let the corpuscle C be now placed on that hand of the plane lGL that is within the solid, and take the distance CK equal to the distance CG. And the part of the solid LGloKO terminated by the parallel planes lGL, oKO, will attract the corpuscle C, situate in the middle, neither one way nor another, the contrary actions of the opposite points destroying one another by reason of their equality. Therefore the corpuscle C is attracted by the force only of the solid situate beyond the plane OK. But this force (by Case 1) is reciprocally as CKn-3, that is, (because CG, CK are equal) reciprocally as CGn-3. Q.E.D.
Cor. 1. Hence if the solid LGIN be terminated on each side by two infinite parallel places LG, IN, its attractive force is known, subducting from the attractive force of the whole infinite solid LGKO the attractive force of the more distant part NIKO infinitely produced towards KO.
Cor. 2. If the more distant part of this solid be rejected, because its attraction compared with the attraction of the nearer part is inconsiderable, the attraction of that nearer part will, as the distance increases, decrease nearly in the ratio of the power CGn-3.
Cor. 3. And hence if any finite body, plane on one side, attract a corpuscle situate over against the middle of that plane, and the distance between the corpuscle and the plane compared with the dimensions of the attracting body be extremely small; and the attracting body consist of homogeneous particles, whose attractive forces decrease in the ratio of any power of the distances greater than the quadruplicate; the attractive force of the whole body will decrease very nearly in the ratio of a power whose side is that very small distance, and the index less by 3 than the index of the former power. This assertion does not hold good, however, of a body consisting of particles whose attractive forces decrease in the ratio of the triplicate power of the distances; because, in that case, the attraction of the remoter part of the infinite body in the second Corollary is always infinitely greater than the attraction of the nearer part.
Scholium.
If a body is attracted perpendicularly towards a given plane, and from the law of attraction given, the motion of the body be required; the Problem will be solved by seeking (by Prop. XXXIX) the motion of the body descending in a right line towards that plane, and (by Cor. 2, of the Laws) compounding that motion with an uniform motion performed in the direction of lines parallel to that plane. And, on the contrary, if there be required the law of the attraction tending towards the plane in perpendicular directions, by which the body may be caused to move in any given curve line, the Problem will be solved by working after the manner of the third Problem.
But the operations may be contracted by resolving the ordinates into
converging series. As if to a base A the length B be ordinately
applied in any given angle, and that length be as any power of the
base A m
n; and there be sought the force with
which a body, either attracted towards the base or driven from it in
the direction of that ordinate, may be caused to move in the curve
line which that ordinate always describes with its superior extremity;
I suppose the base to be increased by a very small part O, and I
resolve the ordinate (A+O)
m
n into an infinite
series Am
n +
m
nOAm
− n
n +
mm − mn
2nnOOAm
− 2n
n &c., and I
suppose the force proportional to the term of this series in which O
is of two dimensions, that is, to the term
mm − mn
2nn OOA
m-2n
n. Therefore the force
sought is as
mm − mn
nn A m-2n
n, or, which is the
same thing, as mm
− mn
nn B m-2n
n. As if the ordinate
describe a parabola, m being = 2, and n = 1, the
force will be as the given quantity 2B°, and therefore is given.
Therefore with a given force the body will move in a parabola, as Galileo
has demonstrated. If the ordinate describe an hyperbola, m
being = 0 − 1, and n = 1, the force will be as 2A-3
or 2B3; and therefore a force which is as the cube of the
ordinate will cause the body to move in an hyperbola. But leaving this
kind of propositions, I shall go on to some others relating to motion
which I have hot yet touched upon.