Section xii.
Of the attractive forces of sphaerical bodies.
Proposition lxx. Theorem xxx.
If to every point of a sphaerical surface there tend equal centripetal forces decreasing in the duplicate ratio of the distances from those points; I say, that a corpuscle placed within that superficies will not be attracted by those forces any way.
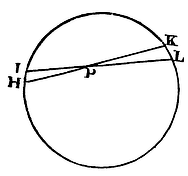
Let HIKL, be that sphaerical superficies, and P a corpuscle placed within. Through P let there be drawn to this superficies to two lines HK, IL, intercepting very small arcs HI, KL; and because (by Cor. 3, Lem. VII) the triangles HPI, LPK are alike, those arcs will be proportional to the distances HP, LP; and any particles at HI and KL of the sphaerical superficies, terminated by right lines passing through P, will be in the duplicate ratio of those distances. Therefore the forces of these particles exerted upon the body P are equal between themselves. For the forces are as the particles directly, and the squares of the distances inversely. And these two ratios compose the ratio of equality. The attractions therefore, being made equally towards contrary parts, destroy each other. And by a like reasoning all the attractions through the whole sphaerical superficies are destroyed by contrary attractions. Therefore the body P will not be any way impelled by those attractions. Q.E.D.
Proposition lxxi. Theorem xxxi.
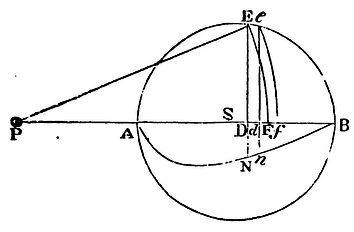
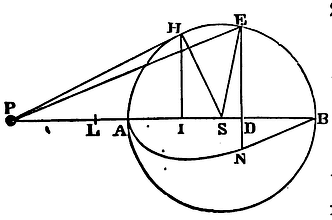
The same things supposed as above, I say, that a corpuscle placed with out the sphaerical superficies is attracted towards the centre of the sphere with a force reciprocally proportional to the square of its distance from that centre.
Let AHKB, ahkb, be two equal sphaerical superficies
described about the centre S, s;
their diameters AB, ab; and let P and p be two
corpuscles situate without the spheres in those diameters produced.
Let there
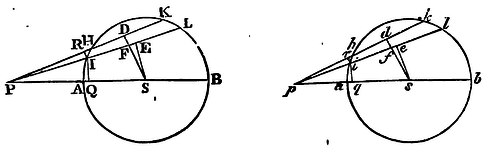 be drawn from the corpuscles the lines PHK, PIL, phk, pil,
cutting off from the great circles AHB,
ahb, the equal arcs HK, hk, IL, il;
and to those lines let fall the perpendiculars SD, sd, SE, se,
IR, ir; of which let SD, sd, cut PL, pl,
in F and f. Let fall also to the diameters the
perpendiculars IQ, iq. Let now the angles DPE, dpe,
vanish; and because DS and ds, ES and es are
equal, the lines PE, PF, and pe, pf, and the lineolao DF, df
may be taken for equal; because their last ratio, when the angles DPE,
dpe vanish together, is the ratio of equality. These things
then supposed, it will be, as PI to PF so is RI to DF, and as pf
to pi so is df or DF to ri; and, ex
aequo, as PI x pf to PF x pi so is RI to ri,
that is (by Cor. 3, Lem VII), so is the arc IH to the arc ih.
Again, PI is to PS as IQ to SE, and ps to pi as se
or SE to iq; and, ex aequo, PI x ps to
PS x pi as IQ to iq. And compounding the ratios
PI² x pf x ps is to pi² x PF x PS, as IH
x IQ to ih x iq; that is, as the circular
superficies which is described by the arc IH, as the semi-circle AKB
revolves about the diameter AB, is to the circular superficies
described by the arc ih as the semi-circle akb
revolves about the diameter ab. And the forces with which
these superficies attract the corpuscles P and p in the
direction of lines tending to those superficies are by the hypothesis
as the superficies themselves directly, and the squares of the
distances of the superficies from those corpuscles inversely; that is,
as pf x ps to PF x PS. And these forces again are
to the oblique parts of them which (by the resolution of forces as in
Cor. 2, of the Laws) tend to the centres in the directions of the
lines PS, ps, as PI to PQ, and pi to pq;
that is (because of the like triangles PIQ and PSF, piq and
psf), as PS to PF and ps to pf. Thence ex
aequo, the attraction of the corpuscle P towards S is to the
attraction of the corpuscle p towards s as
PF x pf x ps
be drawn from the corpuscles the lines PHK, PIL, phk, pil,
cutting off from the great circles AHB,
ahb, the equal arcs HK, hk, IL, il;
and to those lines let fall the perpendiculars SD, sd, SE, se,
IR, ir; of which let SD, sd, cut PL, pl,
in F and f. Let fall also to the diameters the
perpendiculars IQ, iq. Let now the angles DPE, dpe,
vanish; and because DS and ds, ES and es are
equal, the lines PE, PF, and pe, pf, and the lineolao DF, df
may be taken for equal; because their last ratio, when the angles DPE,
dpe vanish together, is the ratio of equality. These things
then supposed, it will be, as PI to PF so is RI to DF, and as pf
to pi so is df or DF to ri; and, ex
aequo, as PI x pf to PF x pi so is RI to ri,
that is (by Cor. 3, Lem VII), so is the arc IH to the arc ih.
Again, PI is to PS as IQ to SE, and ps to pi as se
or SE to iq; and, ex aequo, PI x ps to
PS x pi as IQ to iq. And compounding the ratios
PI² x pf x ps is to pi² x PF x PS, as IH
x IQ to ih x iq; that is, as the circular
superficies which is described by the arc IH, as the semi-circle AKB
revolves about the diameter AB, is to the circular superficies
described by the arc ih as the semi-circle akb
revolves about the diameter ab. And the forces with which
these superficies attract the corpuscles P and p in the
direction of lines tending to those superficies are by the hypothesis
as the superficies themselves directly, and the squares of the
distances of the superficies from those corpuscles inversely; that is,
as pf x ps to PF x PS. And these forces again are
to the oblique parts of them which (by the resolution of forces as in
Cor. 2, of the Laws) tend to the centres in the directions of the
lines PS, ps, as PI to PQ, and pi to pq;
that is (because of the like triangles PIQ and PSF, piq and
psf), as PS to PF and ps to pf. Thence ex
aequo, the attraction of the corpuscle P towards S is to the
attraction of the corpuscle p towards s as
PF x pf x ps
PS is to pf
x PF x ps
ps, that is, as ps² to PS² .
And, by a like reasoning, the forces with which the superficies
described by the revolution of the arcs KL, kl attract those
corpuscles, will be as ps² to PS² . And in the same ratio
will be the forces of all the circular superficies into which each of
the sphaerical superficies may be divided by taking sd
always equal to SD, and se equal to SE. And therefore, by
composition, the forces of the entire sphaerical superficies exerted
upon those corpuscles will be in the same ratio. Q.E.D.
Proposition lxxii. Theorem xxxii.
If to the several points of a sphere there tend equal centripetal forces decreasing in a duplicate ratio of the distances from those points; and there be given both the density of the sphere and the ratio of the diameter of the sphere to the distance of the corpuscle from its centre; I say, that the force with which the corpuscle is attracted is proportional to the semi-diameter of the sphere.
For conceive two corpuscles to be severally attracted by two spheres, one by one, the other by the other, and their distances from the centres of the spheres to be proportional to the diameters of the spheres respectively, and the spheres to be resolved into like particles, disposed in a like situation to the corpuscles. Then the attractions of one corpuscle towards the several particles of one sphere will be to the attractions of the other towards as many analogous particles of the other sphere in a ratio compounded of the ratio of the particles directly, and the duplicate ratio of the distances inversely. But the particles are as the spheres, that is, in a triplicate ratio of the diameters, and the distances are as the diameters; and the first ratio directly with the last ratio taken twice inversely, becomes the ratio of diameter to diameter. Q.E.D.
Cor. 1. Hence if corpuscles revolve in circles about spheres composed of matter equally attracting, and the distances from the centres of the spheres be proportional to their diameters, the periodic times will be equal.
Cor. 2. And, vice versa, if the periodic times are equal, the distances will be proportional to the diameters. These two Corollaries appear from Cor. 3, Prop. IV.
Cor. 3. If to the several points of any two solids whatever, of like figure and equal density, there tend equal centripetal forces decreasing in a duplicate ratio of the distances from those points, the forces, with which corpuscles placed in a like situation to those two solids will be attracted by them, will be to each other as the diameters of the solids.
Proposition lxxiii. Theorem xxxiii.
If to the several points of a given sphere there tend equal centripetal forces decreasing in a duplicate ratio of the distances from the points; I say, that a corpuscle placed within the sphere is attracted by a force proportional to its distance from the centre.
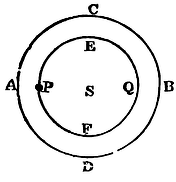
In the sphere ABCD, described about the centre S, let there be placed the corpuscle P; and about the same centre S, with the interval SP, conceive described an interior sphere PEQF. It is plain (by Prop. LXX) that the concentric sphaerical superficies, of which the difference AEBF of the spheres is composed, have no effect at all upon the body P, their attractions being destroyed by contrary attractions. There remains, therefore, only the attraction of the interior sphere PEQF. And (by Prop, LXXII) this is as the distance PS. Q.E.D.
Scholium.
By the superficies of which I here imagine the solids composed, I do not mean superficies purely mathematical, but orbs so extremely thin, that their thickness is as nothing; that is, the evanescent orbs of which the sphere will at last consist when the number of the orbs is increased, and their thickness diminished without end. In like manner, by the points of which lines, surfaces, and solids are said to be composed, are to be understood equal particles, whose magnitude is perfectly inconsiderable.
Proposition lxxiv. Theorem xxxiv.
The same things supposed, I say, that a corpuscle situate without the sphere is attracted with a force reciprocally proportional to the square of its distance from the centre.
For suppose the sphere to be divided into innumerable concentric sphaerical superficies, and the attractions of the corpuscle arising from the several superficies will be reciprocally proportional to the square of the distance of the corpuscle from the centre of the sphere (by Prop. LXXI). And, by composition, the sum of those attractions, that is, the attraction of the corpuscle towards the entire sphere, will be in the same ratio. Q.E.D.
Cor. 1. Hence the attractions of homogeneous spheres at equal distances from the centres will be as the spheres themselves. For (by Prop. LXXII) if the distances be proportional to the diameters of the spheres, the forces will be as the diameters. Let the greater distance be diminished in that ratio; and the distances now being equal, the attraction will be increased in the duplicate of that ratio; and therefore will be to the other attraction in the triplicate of that ratio; that is, in the ratio of the spheres.
Cor. 2. At any distances whatever the attractions are as the spheres applied to the squares of the distances.
Cor. 3. If a corpuscle placed without an homogeneous sphere is attracted by a force reciprocally proportional to the square of its distance from the centre, and the sphere consists of attractive particles, the force of every particle will decrease in a duplicate ratio of the distance from each particle.
Proposition lxxv. Theorem xxxv.
If to the several points of a given sphere there tend equal centripetal forces decreasing in a duplicate ratio of the distances from the points; I say, that another similar sphere will be attracted by it with a force reciprocally proportional to the square of the distance of the centres.
For the attraction of every particle is reciprocally as the square of its distance from the centre of the attracting sphere (by Prop. LXXIV), and is therefore the same as if that whole attracting force issued from one single corpuscle placed in the centre of this sphere. But this attraction is as great as on the other hand the attraction of the same corpuscle would be, if that were itself attracted by the several particles of the attracted sphere with the same force with which they are attracted by it. But that attraction of the corpuscle would be (by Prop. LXXIV) reciprocally proportional to the square of its distance from the centre of the sphere; therefore the attraction of the sphere, equal thereto, is also in the same ratio. Q.E.D.
Cor. 1. The attractions of spheres towards other homogeneous spheres are as the attracting spheres applied to the squares of the distances of their centres from the centres of those which they attract.
Cor. 2. The case is the same when the attracted sphere does also attract. For the several points of the one attract the several points of the other with the same force with which they themselves are attracted by the others again; and therefore since in all attractions (by Law III) the attracted and attracting point are both equally acted on, the force will be doubled by their mutual attractions, the proportions remaining.
Cor. 3. Those several truths demonstrated above concerning the motion of bodies about the focus of the conic sections will take place when an attracting sphere is placed in the focus, and the bodies move without the sphere.
Cor. 4. Those things which were demonstrated before of the motion of bodies about the centre of the conic sections take place when the motions are performed within the sphere.
Proposition lxxvi. Theorem xxxvi.
If spheres be however dissimilar (as to density of matter and attractive force) in the same ratio onward from the centre to the circumference; but every where similar, at every given distance from the centre, on all sides round about; and the attractive force of every point decreases in the duplicate ratio of the distance of the body attracted; I say, that the whole force with which one of these spheres attracts the other will be reciprocally proportional to the square of the distance of the centres.
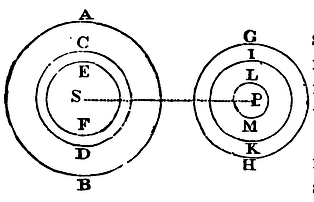
Imagine several concentric similar spheres, AB, CD, EF, &c., the innermost of which added to the outermost may compose a matter more dense towards the centre, or subducted from them may leave the same more lax and rare. Then, by Prop. LXXV, these spheres will attract other similar concentric spheres GH, IK, LM, &c., each the other, with forces reciprocally proportional to the square of the distance SP. And, by composition or division, the sum of all those forces, or the excess of any of them above the others; that is, the entire force with which the whole sphere AB (composed of any concentric spheres or of their differences) will attract the whole sphere GH (composed of any concentric spheres or their differences) in the same ratio. Let the number of the concentric spheres be increased in infinitum, so that the density of the matter together with the attractive force may, in the progress from the circumference to the centre, increase or decrease according to any given law; and by the addition of matter not attractive, let the deficient density be supplied, that so the spheres may acquire any form desired; and the force with which one of these attracts the other will be still, by the former reasoning, in the same ratio of the square of the distance inversely. Q.E.D.
Cor. 1. Hence if many spheres of this kind, similar in all respects, attract each other mutually, the accelerative attractions of each to each, at any equal distances of the centres, will be as the attracting spheres.
Cor. 2. And at any unequal distances, as the attracting spheres applied to the squares of the distances between the centres.
Cor. 3. The motive attractions, or the weights of the spheres towards one another, will be at equal distances of the centres as the attracting and attracted spheres conjunctly; that is, as the products arising from multiplying the spheres into each other.
Cor. 4. And at unequal distances, as those products directly, and the squares of the distances between the centres inversely.
Cor. 5. These proportions take place also when the attraction arises from the attractive virtue of both spheres mutually exerted upon each other. For the attraction is only doubled by the conjunction of the forces, the proportions remaining as before.
Cor. 6. If spheres of this kind revolve about others at rest, each about each; and the distances between the centres of the quiescent and revolving bodies are proportional to the diameters of the quiescent bodies; the periodic times will be equal.
Cor. 7. And, again, if the periodic times are equal, the distances will be proportional to the diameters.
Cor. 8. All those truths above demonstrated, relating to the motions of bodies about the foci of conic sections, will take place when an attracting sphere, of any form and condition like that above described, is placed in the focus.
Cor. 9. And also when the revolving bodies are also attracting spheres of any condition like that above described.
Proposition lxxvii. Theorem xxxvii.
If to the several points of spheres there tend centripetal forces proportional to the distances of the points from the attracted bodies; I say, that the compounded force with which two spheres attract each other mutually is as the distance between the centres of the spheres.
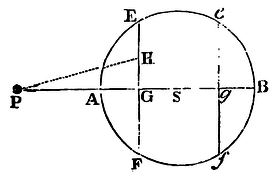
Case 1. Let AEBF be a sphere; S its centre; P a corpuscle attracted; PASB the axis of the sphere passing through the centre of the corpuscle; EF, ef two planes cutting the sphere, and perpendicular to the axis, and equi-distant, one on one side, the other on the other, from the centre of the sphere; G and g the intersections of the planes and the axis; and H any point in the plane EF. The centripetal force of the point H upon the corpuscle P, exerted in the direction of the line PH, is as the distance PH; and (by Cor. 2, of the Laws) the same exerted in the direction of the line PG, or towards the centre S, is as the length PG. Therefore the force of all the points in the plane EF (that is, of that whole plane) by which the corpuscle P is attracted towards the centre S is as the distance PG multiplied by the number of those points, that is, as the solid contained under that plane EF and the distance PG. And in like manner the force of the plane ef, by which the corpuscle P is attracted towards the centre S, is as that plane drawn into its distance Pg, or as the equal plane EF drawn into that distance Pg; and the sum of the forces of both planes as the plane EF drawn into the sum of the distances PG + Pg, that is, as that plane drawn into twice the distance PS of the centre and the corpuscle; that is, as twice the plane EF drawn into the distance PS, or as the sum of the equal planes EF + ef drawn into the same distance. And, by a like reasoning, the forces of all the planes in the whole sphere, equi-distant on each side from the centre of the sphere, are as the sum of those planes drawn into the distance PS, that is, as the whole sphere and the distance PS conjunctly. Q.E.D.
Case 2. Let now the corpuscle P attract the sphere AEBF. And, by the same reasoning, it will appear that the force with which the sphere is attracted is as the distance PS. Q.E.D.
Case 3. Imagine another sphere composed of innumerable corpuscles P; and because the force with which every corpuscle is attracted is as the distance of the corpuscle from the centre of the first sphere, and as the same sphere conjunctly, and is therefore the same as if it all proceeded from a single corpuscle situate in the centre of the sphere, the entire force with which all the corpuscles in the second sphere are attracted, that is, with which that whole sphere is attracted, will be the same as if that sphere were attracted by a force issuing from a single corpuscle in the centre of the first sphere; and is therefore proportional to the distance between the centres of the spheres. Q.E.D.
Case 4. Let the spheres attract each other mutually, and the force will be doubled, but the proportion will remain. Q.E.D.
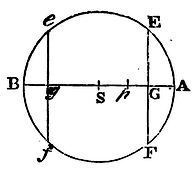
Case 5. Let the corpuscle p be placed within the sphere AEBF; and because the force of the plane ef upon the corpuscle is as the solid contained under that plane and the distance pg; and the contrary force of the plane EP as the solid contained under that plane and the distance pG; the force compounded of both will be as the difference of the solids, that is, as the sum of the equal planes drawn into half the difference of the distances; that is, as that sum drawn into pS, the distance of the corpuscle from the centre of the sphere. And, by a like reasoning, the attraction of all the planes EF, ef, throughout the whole sphere, that is, the attraction of the whole sphere, is conjunctly as the sum of all the planes, or as the whole sphere, and as pS, the distance of the corpuscle from the centre of the sphere. Q.E.D.
Case 6. And if there be composed a new sphere out of innumerable corpuscles such as p, situate within the first sphere AEBF, it may be proved, as before, that the attraction, whether single of one sphere towards the other, or mutual of both towards each other, will be as the distance pS of the centres. Q.E.D.
Proposition lxxviii. Theorem xxxviii.
If spheres is the progress from the centre to the circumference be however dissimilar and unequable, but similar on every side round about at all given distances from the centre; and the attractive force of every point be as the distance of the attracted body; I say, that the entire force with which two spheres of this kind attract each other mutually is proportional to the distance between the centres of the spheres.
This is demonstrated from the foregoing Proposition, in the same manner as Proposition LXXVI was demonstrated from Proposition LXXV.
Cor. Those things that were above demonstrated in Prop. X and LXIV, of the motion of bodies round the centres of conic sections, take place when all the attractions are made by the force of sphaerical bodies of the condition above described, and the attracted bodies are spheres of the same kind.
Scholium.
I have now explained the two principal cases of attractions; to wit, when the centripetal forces decrease in a duplicate ratio of the distances, or increase in a simple ratio of the distances, causing the bodies in both cases to revolve in conic sections, and composing sphaerical bodies whose centripetal forces observe the same law of increase or decrease in the recess from the centre as the forces of the particles themselves do; which is very remarkable. It would be tedious to run over the other cases, whose conclusions are less elegant and important, so particularly as I have done these. I choose rather to comprehend and determine them all by one general method as follows.
Lemma xxix.
If about the centre S there be described any circle as AEB, and about the centre P there be also described two circles EF, ef, cutting the first in E And e, and the line PS in F and f; and there be let fall to PS the perpendiculars ED, ed; I say, that if the distance of the arcs EF, ef be supposed to be infinitely diminished, the last ratio of the evanscent line Dd to the evanescent line Ff is the same as that of the line PE to the line PS.
For if the line Pe cut the arc EF in q; and the
right line Ee, which
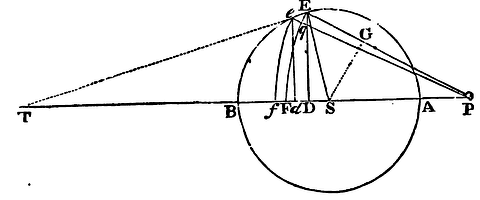 coincides with the evanescent arc Ee, be produced, and meet the right
line PS in T; and there be let fall from S to PE the perpendicular SG;
then, because of the like triangles DTE, dTe, DES,
it will be as Dd to Ee so DT to TE, or DE to ES: and
because the triangles, Eeq, ESG (by Lem. VIII, and Cor. 3,
Lem. VII) are similar, it will be as Ee to eq or Ff
so ES to SG; and, ex aequo, as Dd to Ff so
DE to SG; that is (because of the similar triangles PDE, PGS), so is
PE to PS. Q.E.D.
coincides with the evanescent arc Ee, be produced, and meet the right
line PS in T; and there be let fall from S to PE the perpendicular SG;
then, because of the like triangles DTE, dTe, DES,
it will be as Dd to Ee so DT to TE, or DE to ES: and
because the triangles, Eeq, ESG (by Lem. VIII, and Cor. 3,
Lem. VII) are similar, it will be as Ee to eq or Ff
so ES to SG; and, ex aequo, as Dd to Ff so
DE to SG; that is (because of the similar triangles PDE, PGS), so is
PE to PS. Q.E.D.
Proposition lxxix. Theorem xxxix.
Suppose a superficies as EFfe to have its breadth infinitely diminished, and to be just vanishing and that the same superficies by its revolution round the axis PS describes a sphaerical concavo-convex solid, to the several equal particles of which there tend equal centripetal forces; I say, that the force with which that solid attracts a corpuscle situate in P Is in a ratio compounded of the ratio of the solid DE² x Ff And the ratio of the force with which the given particle in the place Ff would, attract the same corpuscle.
For if we consider, first, the force of the sphaerical superficies FE which
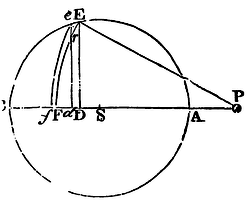 is generated by the revolution of the arc FE, and is cut any where, as in
r, by the line de, the annular part of the
superficies generated by the revolution of the arc rE will
be as the lineola Dd, the radius of the sphere PE remaining
the same; as Archimedes has demonstrated in his Book of the
Sphere and Cylinder. And the force of this superficies exerted in the
direction of the lines PE or Pr situate all round in the
conical superficies, will be as this annular superficies itself; that
is as the lineola Dd, or, which is the same, as the rectangle
under the given radius PE of the sphere and the lineola Dd;
but that force, exerted in the direction of the line PS tending to the
centre S, will be less in the ratio PD to PE, and therefore will be as
PD x Dd. Suppose now the line DF to be divided into
innumerable little equal particles, each of which call Dd,
and then the superficies FE will be divided into so many equal annuli,
whose forces will be as the sum of all the rectangles PD x Dd,
that is, as ½PF² − ½PD², and therefore as DE². Let now the superficies
FE be drawn into the altitude Ff; and the force of the solid
EFfe exerted upon the corpuscle P will be as DE² x Ff;
that is, if the force be given which any given particle as Ff
exerts upon the corpuscle P at the distance PF. But if that force be
not given, the force of the solid EFfe will be as the solid
DE² x Ff and that force not given, conjunctly.
Q.E.D.
is generated by the revolution of the arc FE, and is cut any where, as in
r, by the line de, the annular part of the
superficies generated by the revolution of the arc rE will
be as the lineola Dd, the radius of the sphere PE remaining
the same; as Archimedes has demonstrated in his Book of the
Sphere and Cylinder. And the force of this superficies exerted in the
direction of the lines PE or Pr situate all round in the
conical superficies, will be as this annular superficies itself; that
is as the lineola Dd, or, which is the same, as the rectangle
under the given radius PE of the sphere and the lineola Dd;
but that force, exerted in the direction of the line PS tending to the
centre S, will be less in the ratio PD to PE, and therefore will be as
PD x Dd. Suppose now the line DF to be divided into
innumerable little equal particles, each of which call Dd,
and then the superficies FE will be divided into so many equal annuli,
whose forces will be as the sum of all the rectangles PD x Dd,
that is, as ½PF² − ½PD², and therefore as DE². Let now the superficies
FE be drawn into the altitude Ff; and the force of the solid
EFfe exerted upon the corpuscle P will be as DE² x Ff;
that is, if the force be given which any given particle as Ff
exerts upon the corpuscle P at the distance PF. But if that force be
not given, the force of the solid EFfe will be as the solid
DE² x Ff and that force not given, conjunctly.
Q.E.D.
Proposition lxxx. Theorem xl.
If to the several equal parts of a sphere ABE described
about the centre S there tend equal centripetal forces; and from
the several points D in the axis of the sphere AB in
which a corpuscle, as F, is placed, there be erected the
perpendiculars DE meeting the sphere in E, and
if in those perpendiculars the lengths DN be taken as
the quantity DE2
x PS
PE, and as the force which a particle of the sphere
situate in the axis exerts at the distance PE upon the
corpuscle P conjunctly; I say, that the whole force with
which the corpuscle P is attracted towards the sphere is
as the area ANB, comprehended under the axis of the
sphere AB, and the crrve line ANB, the locus of the point N.
For supposing the construction in the last Lemma and Theorem to
stand, conceive the axis of the sphere AB to be divided into
innumerable equal particles Dd, and the whole sphere to be
divided into so many sphserical concavo-convex laminae EFfe;
and erect the perpendicular dn. By the last Theorem, the
force with which the laminae EFfe attracts the corpuscle P
is as DE² x Ff and the force of one particle exerted at the
 distance PE or PF, conjunctly. But (by the last Lemma) Dd is to Ff as PE to PS,
and therefore Ff is equal to PS
x Dd
distance PE or PF, conjunctly. But (by the last Lemma) Dd is to Ff as PE to PS,
and therefore Ff is equal to PS
x Dd
PE; and DE² x Ff is equal to Dd
x DE2 x PS
PE; and therefore the force of the lamina EFfe
is as Dd x DE2
x PS
PE and the force of a particle exerted at the
distance PF conjunctly; that is, by the supposition, as DN x Dd,
or as the evanescent area DNnd. Therefore the forces of all
the laminae exerted upon the corpuscle P are as all the areas DNnd,
that is, the whole force of the sphere will be as the whole area ANB.
Q.E.D.
Cor. 1. Hence if the centripetal force
tending to the several particles remain always the same at all
distances, and DN be made as DE2
x PS
PE the whole force with which the corpuscle is attracted by
the sphere is as the area ANB.
Cor. 2. If the centripetal force of the
particles be reciprocally as the distance of the corpuscle attracted
by it, and DN be made as DE2
x PS
PE2, the force with which the corpuscle P is
attracted by the whole sphere will be as the area ANB.
Cor. 3. If the centripetal force of the
particles be reciprocally as the cube of the distance of the corpuscle
attracted by it, and DN be made as DE2
x PS
PE4, the force with which the corpuscle is
attracted by the whole sphere will be as the area ANB.
Cor. 4. And universally if the centripetal
force tending to the several particles of the sphere be supposed to be
reciprocally as the quantity V; and DN be made as
DE2 x PS
PE x V; the force with which a corpuscle is attracted by the
whole sphere will be as the area ANB.
Proposition lxxxi. Problem xli.
The things remaining as above, it is required to measure the area ANB.
From the point P let there be drawn the right line PH touching the
sphere in H; and to the axis PAB, letting fall the perpendicular HI,
bisect PI in L; and (by Prop. XII, Book II, Elem.) PE² is equal to
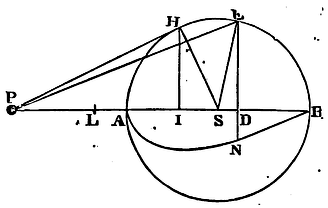 PS² + SE² + 2PSD. But because the triangles SPH,
SHI are alike, SE² or SH² is equal to the rectangle PSI.
Therefore PE² is equal to the rectangle contained under PS and PS
+ SI + 2SD; that is, under PS and 2LS + 2SD; that is, under PS and
2LD. Moreover DE² is equal to SE² − SD², or SE² − LS² + 2SLD − LD²,
that is, 2SLD − LD² − ALB. For LS² − SE² or LS² − SA² (by Prop. VI,
Book II, Elem.) is equal to the rectangle ALB. Therefore if instead of
DE² we write 2SLD − LD² − ALB, the quantity
DE2 x PS
PS² + SE² + 2PSD. But because the triangles SPH,
SHI are alike, SE² or SH² is equal to the rectangle PSI.
Therefore PE² is equal to the rectangle contained under PS and PS
+ SI + 2SD; that is, under PS and 2LS + 2SD; that is, under PS and
2LD. Moreover DE² is equal to SE² − SD², or SE² − LS² + 2SLD − LD²,
that is, 2SLD − LD² − ALB. For LS² − SE² or LS² − SA² (by Prop. VI,
Book II, Elem.) is equal to the rectangle ALB. Therefore if instead of
DE² we write 2SLD − LD² − ALB, the quantity
DE2 x PS
PE x V, which (by Cor. 4 of the foregoing Prop.) is as the
length of the ordinate DN, will now resolve itself into three parts
2SLD x PS
PE x V − LD2
x PS
PE x V − ALB
x PS
PE x V; where if instead of V
we write the inverse ratio of the centripetal force, and instead of PE
the mean proportional between PS and 2LD, those three parts will
become ordinates to so many curve lines, whose areas are discovered by
the common methods. Q.E.D.
Example 1. If the centripetal force tending
to the several particles of the sphere be reciprocally as the
distance; instead of V write PE the distance, then 2PS x LD for PE²;
and DN will become as SL − ½LD − ALB
2LD. Suppose DN equal to its double 2SL
− LD − ALB
LD; and 2SL the given part of the
ordinate drawn into the length AB will describe the rectangular area
2SL x AB; and the indefinite part LD, drawn perpendicularly into the
same length with a continued motion, in such sort as in its motion one
way or another it may either by increasing or decreasing remain always
equal to the length LD, will describe the area
LB2 − LA2
2, that is, the area SL x AB; which
taken from the former area 2SL x AB, leaves the area SL x AB. But the
third part ALB
LD, drawn after the same manner with a
continued motion perpendicularly into the same length,
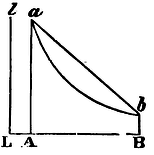 will describe the area of an hyperbola, which subducted from the area
SL x AB will leave ANB the area sought. Whence arises this
construction of the Problem. At the points, L, A, B, erect the
perpendiculars Ll, Aa, Bb; making Aa
equal to LB, and Bb equal to LA. Making Ll and LB
asymptotes, describe through the points a, b, the
hyperbolic curve ab. And the chord ba being drawn,
will inclose the area aba equal to the area sought ANB.
will describe the area of an hyperbola, which subducted from the area
SL x AB will leave ANB the area sought. Whence arises this
construction of the Problem. At the points, L, A, B, erect the
perpendiculars Ll, Aa, Bb; making Aa
equal to LB, and Bb equal to LA. Making Ll and LB
asymptotes, describe through the points a, b, the
hyperbolic curve ab. And the chord ba being drawn,
will inclose the area aba equal to the area sought ANB.
Example 2. If the centripetal force tending
to the several particles of the sphere be reciprocally as the cube of
the distance, or (which is the same thing) as that cube applied to any
given plane; write PE3
2AS2 for V, and 2PS x LD for
PE²; and DN will become as
SL x AS2
PS x LD − AS2
2PS − ALB
x AS2
2PS x LD2 that is
(because PS, AS, SI are continually proportional), as
LSI
LD − 1/2SI
− ALB x SI
2LD2. If we draw
then these three parts into the length AB, the first
LSI
LD will generate the area of an
hyperbola; the second ½SI the area ½AB x SI; the third
ALB x SI
2LD2 the area
ALB x SI
2LA ALB
x SI
2LB, that is, ½AB x SI. From the first
subduct the sum of the second and third, and there will remain ANB,
the area sought. Whence arises this construction of the problem. At
the points L, A, S, B, erect
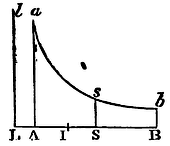 the perpendiculars Ll Aa Ss, Bb, of
which suppose Ss equal to SI; and through the point s,
to the asymptotes Ll, LB, describe the hyperbola asb
meeting the perpendiculars Aa, Bb, in a
and b; and the rectangle 2ASI, subducted from the hyberbolic
area AasbB, will leave ANB the area sought.
the perpendiculars Ll Aa Ss, Bb, of
which suppose Ss equal to SI; and through the point s,
to the asymptotes Ll, LB, describe the hyperbola asb
meeting the perpendiculars Aa, Bb, in a
and b; and the rectangle 2ASI, subducted from the hyberbolic
area AasbB, will leave ANB the area sought.
Example 3. If the centripetal force tending
to the several particles of the spheres decrease in a quadruplicate
ratio of the distance from the particles; write
PE4
2AS3 for V, then √(2PS+LD)
for PE, and DN will become as
SI2 x SL
√(2SI) x 1
√LD3 −
SI2
2√(2SI) x 1
√LD − SI2
x ALB
2√(2SI) x 1
√LD5. These three
parts drawn into the length AB, produce so many areas, viz.
 2SI2 x SL
2SI2 x SL
√(2SI) into (
1
√(LA) − 1
√(LB) );
SI2
√(2SI) into √LB −
√LA; and SI2
x ALB
3√(2SI) into (
1
√(LA3) −
1
√(LB3) ). And
these after due reduction come forth 2SI2
x SL
LI, SI², and SI² +
2SI3
3LI. And these by subducting the last
from the first, become 4SI3
3LI. Therefore the entire force with
which the corpuscle P is attracted towards the centre of the sphere is
as SI3
PI, that is, reciprocally as PS³ x PI.
Q.E.I.
By the same method one may determine the attraction of a corpuscle situate within the sphere, but more expeditiously by the following Theorem.
Proposition lxxxii. Theorem xli.
In a sphere described about the centre S with the interval SA, if there be taken SI, SA, SP continually proportional; I say, that the attraction of a corpuscle within the sphere in any place I is to its attraction without the sphere in the place P in a ratio compounded of the subduplicate ratio of IS, PS, the distances from the centre, and the subduplicate ratio of the centripetal forces tending to the centre in those places P and I.
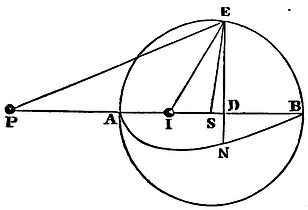
As if the centripetal forces of the particles of the sphere be reciprocally as the distances of the corpuscle attracted by them; the force with which the corpuscle situate in I is attracted by the entire sphere will be to the force with which it is attracted in P in a ratio compounded of the subduplicate ratio of the distance SI to the distance SP, and the subduplicate ratio of the centripetal force in the place I arising from any particle in the centre to the centripetal force in the place P arising from the same particle in the centre; that is, in the subduplicate ratio of the distances SI, SP to each other reciprocally. These two subduplicate ratios compose the ratio of equality, and therefore the attractions in I and P produced by the whole sphere are equal. By the like calculation, if the forces of the particles of the sphere are reciprocally in a duplicate ratio of the distances, it will be found that the attraction in I is to the attraction in P as the distance SP to the semi-diameter SA of the sphere. If those forces are reciprocally in a triplicate ratio of the distances, the attractions in I and P will be to each other as SP² to SA²; if in a quadruplicate ratio, as SP³ to SA³. Therefore since the attraction in P was found in this last case to be reciprocally as PS³ x PI, the attraction in I will be reciprocally as SA³ x PI, that is, because SA³ is given reciprocally as PI. And the progression is the same in infinitum. The demonstration of this Theorem is as follows:
The things remaining as above constructed, and a corpuscle being in
any place P, the ordinate DN was found to be
as DE2 x PS
PE x V. Therefore if IE be drawn, that
ordinate for any other place of the corpuscle, as I, will become (mutatis
mutandis) as DE2
x IS
IE x V. Suppose the centripetal forces
flowing from any point of the sphere, as E, to be to each other at the
distances IE and PE as PEn to IEn (where the
number n denotes the index of the powers of PE and IE), and
those ordinates will become as DE2
x PS
PE x PEn and
DE2 x IS
IE x IEn whose ratio to each
other is as PS x IE x IEn to
IS x PE x PEn. Because SI, SE, SP are
in continued proportion, the triangles SPE, SEI are alike; and thence
IE is to PE as IS to SE or SA. For the ratio of IE to PE write the
ratio of IS to SA; and the ratio of the ordinates becomes that of PS x
IEn to SA x PEn. But the ratio of PS to SA is
subduplicate of that of the distances PS, SI; and the ratio of IEn
to PEn (because IE is to PE as IS to SA) is subduplicate of
that of the forces at the distances PS, IS. Therefore the ordinates,
and consequently the areas which the ordinates describe, and the
attractions proportional to them, are in a ratio compounded of those
subduplicate ratios. Q.E.D.
Proposition lxxxiii. Problem xlii.
To find the force with which a corpuscle placed in the centre of a sphere is attracted towards any segment of that sphere whatsoever.
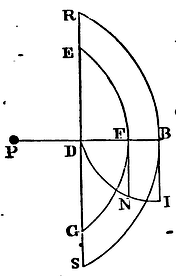
Let P be a body in the centre of that sphere and RBSD a segment
thereof contained under the plane RDS, and thesphaerical superficies
RBS. Let DB be cut in F by a sphaerical superficies EFG described from
the centre P, and let the segment be divided into the parts BREFGS,
FEDG. Let us suppose that segment to be not a purely mathematical but
a physical superficies, having some, but a perfectly inconsiderable
thickness. Let that thickness be called O, and (by what Archimedes
has demonstrated) that superficies will be as PF x DF x O. Let us
suppose besides the attractive forces of the particles of the sphere
to be reciprocally as that power of the distances, of which n
is index; and the force with which the superficies EFG attracts the
body P will be (by Prop. LXXIX) as DE2
x O
PFn, that is, as
2DF x O
PF(n-1) −
DF2 x O
PFn. Let the
perpendicular FN drawn into O be proportional
to this quantity; and the curvilinear area BDI, which the ordinate FN,
drawn through the length DB with a continued motion will describe,
will be as the whole force with which the whole segment RBSD attracts
the body P. Q.E.I.
Proposition lxxxiv. Problem xliii.
To find the force with which a corpuscle, placed without the centre of a sphere in the axis of any segment, is attracted by that segment.
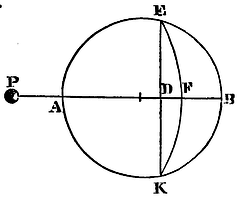
Let the body P placed in the axis ADB of the segment EBK be attracted by that segment. About the centre P, with the interval PE, let the spherical superficies EFK be described; and let it divide the segment into two parts EBKFE and EFKDE. Find the force of the first of those parts by Prop. LXXXI, and the force of the latter part by Prop. LXXXIII, and the sum of the forces will be the force of the whole segment EBKDE. Q.E.I.
Scholium.
The attractions of sphaerical bodies being now explained, it comes next in order to treat of the laws of attraction in other bodies consisting in like manner of attractive particles; but to treat of them particularly is not necessary to my design. It will be sufficient to subjoin some general propositions relating to the forces of such bodies, and the motions thence arising, because the knowledge of these will be of some little use in philosophical inquiries.