Section xiv.
Of the motion of very small bodies when agitated by centripetal forces tending to the several parts of any very great body.
Proposition xciv. Theorem xlviii.
If two similar mediums be separated from each other by a space terminated on both sides by parallel planes, and a body in its passage through that space be attracted or impelled perpendicularly towards either of those mediums, and not agitated or hindered by any other force; and the attraction be every where the same at equal distances from either plane, taken towards the same hand of the plane; I say, that the sine of incidence upon either plane will be to the sine of emergence of the other plane in a given ratio.
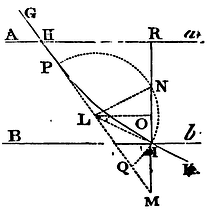
Case 1. Let Aa and Bb be two parallel planes, and let the body light upon the first plane Aa in the direction of the line GH, and in its whole passage through the intermediate space let it be attracted or impelled towards the medium of incidence, and by that action let it be made to describe a curve line HI, and let it emerge in the direction of the line IK. Let there be erected IM perpendicular to Bb the plane of emergence, and meeting the line of incidence GH prolonged in M, and the plane of incidence Aa in R; and let the line of emergence KI be produced and meet HM in L. About the centre L, with the interval LI, let a circle be described cutting both HM in P and Q, and MI produced in N; and, first, if the attraction or impulse be supposed uniform, the curve HI (by what Galileo has demonstrated) be a parabola, whose property is that of a rectangle under its given latus rectum and the line IM is equal to the square of HM; and moreover the line HM will be bisected in L. Whence if to MI there be let fall the perpendicular LO, MO, OR will be equal: and adding the equal lines ON, OI, the wholes MN, IR will be equal also. Therefore since IR is given, MN is also given, and the rectangle NMI is to the rectangle under the latus rectum and IM, that is, to HM² in a given ratio. But the rectangle NMI is equal to the rectangle PMQ, that is, to the difference of the squares ML², and PL² or LI²; and HM² hath a given ratio to its fourth part ML²; therefore the ratio of ML² − LI² to ML² is given, and by conversion the ratio of LI² to ML², and its subduplicate, the ratio of LI to ML. But in every triangle, as LMI, the sines of the angles are proportional to the opposite sides. Therefore the ratio of the sine of the angle of incidence LMR to the sine of the angle of emergence LIR is given. Q.E.D.
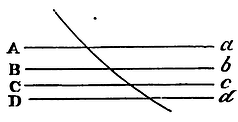
Case 2. Let now the body pass successively through several spaces terminated with parallel planes AabB, EbcC, &c., and let it be acted on by a force which is uniform in each of them separately, but different in the different spaces; and by what was just demonstrated, the sine of the angle of incidence on the first plane Aa is to the sine of emergence from the second plane Bb in a given ratio; and this sine of incidence upon the second plane Bb will be to the sine of emergence from the third plane Cc in a given ratio; and this sine to the sine of emergence from the fourth plane Dd in a given ratio; and so on in infinitum; and, by equality, the sine of incidence on the first plane to the sine of emergence from the last plane in a given ratio. Let now the intervals of the planes be diminished, and their number be infinitely increased, so that the action of attraction or impulse, exerted according to any assigned law, may become continual, and the ratio of the sine of incidence on the first plane to the sine of emergence from the last plane being all along given, will be given then also. Q.E.D.
Proposition xcv. Theorem xlix.
The same things being supposed, I say, that the velocity of the body before its incidence is to its velocity after emergence as the sine of emergence to the sine of incidence.
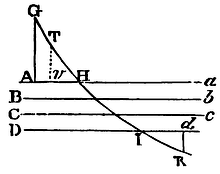
Make AH and Id equal, and erect the perpendiculars AG, dK meeting the lines of incidence and emergence GH, IK, in G and K. In GH take TH equal to IK, and to the plane Aa let fall a perpendicular Tv. And (by Cor. 2 of the Laws of Motion) let the motion of the body be resolved into two, one perpendicular to the planes Aa, Bb, Cc, &c, and another parallel to them. The force of attraction or impulse, acting in directions perpendicular to those planes, does not at all alter the motion in parallel directions; and therefore the body proceeding with this motion will in equal times go through those equal parallel intervals that lie between the line AG and the point H, and between the point I and the line dK; that is, they will describe the lines GH, IK in equal times. Therefore the velocity before incidence is to the velocity after emergence as GH to IK or TH, that is, as AH or Id to vH; that is (supposing TH or IK radius), as the sine of emergence to the sine of incidence. Q.E.D.
Proposition xcvi. Theorem L.
The same things being supposed, and that the motion before incidence is swifter than afterwards; I say, that if the line of incidence be inclined continually, the body will be at last reflected, and the angle of reflexion will be equal to the angle of incidence.
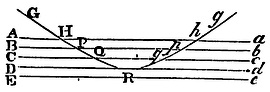
For conceive the body passing between the parallel planes Aa, Bb, Cc, &c., to describe parabolic arcs as above; and let those arcs be HP, PQ, QR, &c. And let the obliquity of the line of incidence GH to the first plane Aa be such that the sine of incidence may be to the radius of the circle whose sine it is, in the same ratio which the same sine of incidence hath to the sine of emergence from the plane Dd into the space DdeE; and because the sine of emergence is now become equal to radius, the angle of emergence will be a right one, and therefore the line of emergence will coincide with the plane Dd. Let the body come to this plane in the point R; and because the line of emergence coincides with that plane, it is manifest that the body can proceed no farther towards the plane Ee. But neither can it proceed in the line of emergence Rd; because it is perpetually attracted or impelled towards the medium of incidence. It will return, therefore, between the planes Cc, Dd, describing an arc of a parabola QRq, whose principal vertex (by what Galileo has demonstrated) is in R, cutting the plane Cc in the same angle at q, that it did before at Q; then going on in the parabolic arcs qp, ph, &c., similar and equal to the former arcs QP, PH, &c., it will cut the rest of the planes in the same angles at p, h, &c., as it did before in P, H, &c., and will emerge at last with the same obliquity at h with which it first impinged on that plane at H. Conceive now the intervals of the planes Aa, Bb, Cc, Dd, Ee, &c., to be infinitely diminished, and the number in finitely increased, so that the action of attraction or impulse, exerted according to any assigned law, may become continual; and, the angle of emergence remaining all along equal to the angle of incidence, will be equal to the same also at last. Q.E.D.
Scholium.
These attractions bear a great resemblance to the reflexions and
refractions of light made in a given ratio of the secants, as was
discovered by Snellius; and consequently in a given ratio of
the sines, as was exhibited by Des Cartes. For it is now
certain from the phenomena of Jupiter's Satellites,
confirmed by the observations of different astronomers, that light is
propagated in succession, and requires about seven or eight minutes to
travel from the sun to the earth. Moreover, the rays of light that are
in our air (as lately was discovered by Grimaldus, by the
admission of light into a dark room through a small hole, which I have
also tried) in their passage near the angles of bodies, whether
transparent or opaque (such as the circular and rectangular edges of
gold, silver and brass coins, or of knives, or broken pieces of stone
or glass), are bent or inflected round those bodies as if they were
attracted to them; and those rays which in their passage come nearest
to the bodies are the most inflected, as if they were most attracted:
which tiling I myself have also carefully observed. And those which
pass at greater distances are less inflected; and those at still
greater distances are a little inflected the contrary way, and form
three fringes of colours. In the figure s represents the
edge of a knife, or any
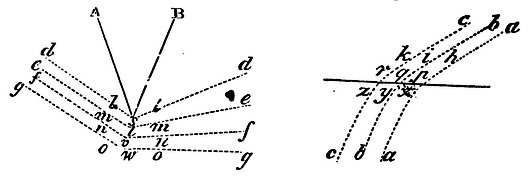 kind of wedge AsB; and gowog, fnunf, emtme,
dlsld, are rays inflected towards the knife in the arcs owo,
nvn, mtm, lsl; which inflection is greater or less according to
their distance from the knife. Now since this inflection of the rays
is performed in the air without the knife, it follows that the rays
which fall upon the knife are first inflected in the air before they
touch the knife. And the case is the same of the rays falling upon
glass. The refraction, therefore, is made not in the point of
incidence, but gradually, by a continual inflection of the rays: which
is done partly in the air before they touch the glass, partly (if I
mistake not) within the glass, after they have entered it; as is
represented in the rays ckzc, biyb, ahxa, falling upon r,
q, p, and inflected between k and z, i and
y, h and x. Therefore because of the analogy there
is between the propagation of the rays of light and the motion of
bodies, I thought it not amiss to add the following Propositions for
optical uses: not at all considering the nature of the rays of light,
or inquiring whether they are bodies or not; but only determining the
trajectories of bodies which are extremely like the trajectories of
the rays.
kind of wedge AsB; and gowog, fnunf, emtme,
dlsld, are rays inflected towards the knife in the arcs owo,
nvn, mtm, lsl; which inflection is greater or less according to
their distance from the knife. Now since this inflection of the rays
is performed in the air without the knife, it follows that the rays
which fall upon the knife are first inflected in the air before they
touch the knife. And the case is the same of the rays falling upon
glass. The refraction, therefore, is made not in the point of
incidence, but gradually, by a continual inflection of the rays: which
is done partly in the air before they touch the glass, partly (if I
mistake not) within the glass, after they have entered it; as is
represented in the rays ckzc, biyb, ahxa, falling upon r,
q, p, and inflected between k and z, i and
y, h and x. Therefore because of the analogy there
is between the propagation of the rays of light and the motion of
bodies, I thought it not amiss to add the following Propositions for
optical uses: not at all considering the nature of the rays of light,
or inquiring whether they are bodies or not; but only determining the
trajectories of bodies which are extremely like the trajectories of
the rays.
Proposition xcvii. Problem xlvii.
Supposing the sine of incidence upon any superficies to be in a given ratio to the sine of emergence; and that the inflection of the paths of those bodies near that superficies is performed in a very short space, which may be considered as a point; it is required to determine such a superficies as may cause all the corpuscles issuing from any one given place to converge to another given place.
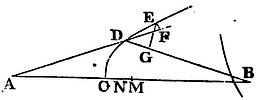
Let A be the place from whence the corpuscles diverge; B the place to which they should converge; CDE the curve line which by its revolution round the axis AB describes the superficies sought; D, E, any two points of that curve: and EF, EG, perpendiculars let fall on the paths of the bodies AD, DB. Let the point D approach to and coalesce with the point E; and the ultimate ratio of the line DF by which AD is increased, to the line DG by which DB is diminished, will be the same as that of the sine of incidence to the sine of emergence. Therefore the ratio of the increment of the line AD to the decrement of the line DB is given; and therefore if in the axis AB there be taken any where the point C through which the curve CDE must pass, and CM the increment of AC be taken in that given ratio to CN the decrement of BC, and from the centres A, B, with the intervals AM, BN, there be described two circles cutting each other in D; that point D will touch the curve sought CDE, and, by touching it any where at pleasure, will determine that curve. Q.E.I.
Cor. 1. By causing the point A or B to go off sometimes in infinitum, and sometimes to move towards other parts of the point C, will be obtained all those figures which Cartesius has exhibited in his Optics and Geometry relating to refractions. The invention of which Cartesius having thought fit to conceal, is here laid open in this Proposition.
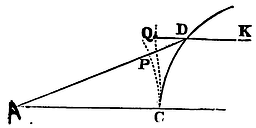
Cor. 2. If a body lighting on any superficies CD in the direction of a right line AD, drawn according to any law, should emerge in the direction of another right line DK; and from the point C there be drawn curve lines CP, CQ, always perpendicular to AD, DK; the increments of the lines PD, QD, and therefore the lines themselves PD, QD, generated by those increments, will be as the sines of incidence and emergence to each other, and è contra.
Proposition xcviii. Problem xlviii.
The same things supposed; if round the axis AB any attractive superficies be described as CD, regular or irregular, through which the bodies issuing from the given place A must pass; it is required to find a second attractive superficies EF, which may make those bodies converge to a given place B.
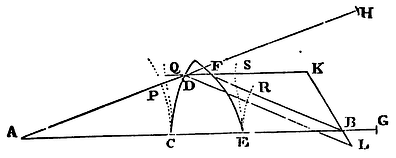
Let a line joining AB cut the first superficies in C and the second in E, the point D being taken any how at pleasure. And supposing the sine of incidence on the first superficies to the sine of emergence from the same, and the sine of emergence from the second superficies to the sine of incidence on the same, to be as any given quantity M to another given quantity N; then produce AB to G, so that BG may be to CE as M − N to N; and AD to H, so that AH may be equal to AG; and DF to K, so that DK may be to DH as N to M. Join KB, and about the centre D with the interval DH describe a circle meeting KB produced in L, and draw BF parallel to DL; and the point F will touch the line EF, which, being turned round the axis AB, will describe the superficies sought. Q.E.F.
For conceive the lines CP, CQ, to be every where perpendicular to AD, DF, and the lines ER, ES to FB, FD respectively, and therefore QS to be always equal to CE; and (by Cor. 2, Prop. XCVII) PD will be to QD as M to N, and therefore as DL to DK, or FB to FK; and by division as DL − FB or PH − PD − FB to FD or FQ − QD; and by composition as PH − FB to FQ, that is (because PH and CG, QS and CE, are equal), as CE + BG − FR to CE − FS. But (because BG is to CE as M − N to N) it comes to pass also that CE + BG is to CE as M to N; and therefore, by division, FR is to FS as M to N; and therefore (by Cor. 2, Prop XCVII) the superficies EF compels a body, falling upon it in the direction DF, to go on in the line FR to the place B. Q.E.D.
Scholium.
In the same manner one may go on to three or more superficies. But of all figures the spherical is the most proper for optical uses. If the object glasses of telescopes were made of two glasses of a sphaerical figure, containing water between them, it is not unlikely that the errors of the refractions made in the extreme parts of the superficies of the glasses may be accurately enough corrected by the refractions of the water. Such object glasses are to be preferred before elliptic and hyperbolic glasses, not only because they may be formed with more ease and accuracy, but because the pencils of rays situate without the axis of the glass would be more accurately refracted by them. But the different refrangibility of different rays is the real obstacle that hinders optics from being made perfect by sphaerical or any other figures. Unless the errors thence arising can be corrected, all the labour spent in correcting the others is quite thrown away.