Section ix.
Of the motion of bodies in moveable orbits; and of the motion of the apsides.
Proposition xliii. Problem xxx.
It is required to make a body move in a trajectory that revolves about the centre of force in the same manner as another body in the same trajectory at rest.
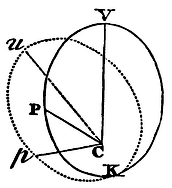
In the orbit VPK, given by position, let the body P revolve, proceeding from V towards K. From the centre C let there be continually drawn Cp, equal to CP, making the angle VCp proportional to the angle VCP; and the area which the line Cp describes will be to the area VCP, which the line CP describes at the same time, as the velocity of the describing line Cp to the velocity of the describing line CP; that is, as the angle VCp to the angle VCP, therefore in a given ratio, and therefore proportional to the time. Since, then, the area described by the line Cp in an immovable plane is proportional to the time, it is manifest that a body, being acted upon by a just quantity of centripetal force may revolve with the point p in the curve line which the same point p, by the method just now explained, may be made to describe an immovable plane. Make the angle VCu equal to the angle PCp, and the line Cu equal to CV, and the figure uCp equal to the figure VCP, and the body being always in the point p, will move in the perimeter of the revolving figure uCp, and will describe its (revolving) arc up in the same time that the other body P describes the similar and equal arc VP in the quiescent figure VPK. Find, then, by Cor. 5, Prop. VI., the centripetal force by which the body may be made to revolve in the curve line which the point p describes in an immovable plane, and the Problem will be solved. Q.E.F.
Proposition xliv. Theorem xiv.
The difference of the forces, by which two bodies may be made to move equally, one in a quiescent, the other in the same orbit revolving, is in a triplicate ratio of their common altitudes inversely.
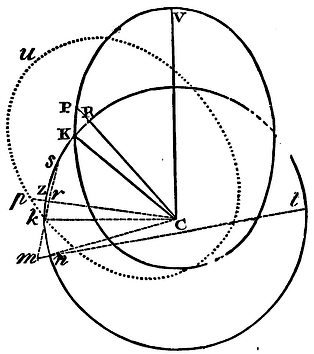
Let the parts of the quiescent orbit VP, PK be similar and equal to
the parts of the revolving orbit up, pk; and let the
distance of the points P and K be supposed of the utmost smallness.
Let fall a perpendicular kr from the point k to
the right line pC, and produce it to m, so that mr
may be to kr as the angle VCp to the angle VCP.
Because the altitudes of the bodies PC and pC, KC and kC,
are always equal, it is manifest that the increments or decrements of
the lines PC and pC are always equal; and therefore if each
of the several motions of the bodies in the places P and p
be resolved into two (by Cor. 2 of the Laws of Motion), one of which
is directed towards the centre, or according to the lines PC, pC,
and the other, transverse to the former, hath a direction
perpendicular to the lines PC and pC; the motions towards
the centre will be equal, and the transverse motion of the body p
will be to the transverse motion of the body P as the angular motion
of the line pC to the angular motion of the line PC; that
is, as the angle VCp to the angle VCP. Therefore, at the same
time that the body P, by both its motions, comes to the point K, the
body p, having an equal motion towards the centre, will be
equally moved from p towards C; and therefore that time
being expired, it will be found somewhere in the line mkr,
which, passing through the point k, is perpendicular to the
line pC; and by its transverse motion will acquire a
distance from the line pC, that will
be to the distance which the other body P acquires from the line PC as
the transverse motion of the body p to the transverse motion
of the other body P. Therefore since kr is equal to the
distance which the body P acquires from the line PC, and mr
is to kr as the angle VCp to the angle VCP, that
is, as the transverse motion of the body p to the transverse
motion of the body P, it is manifest that the body p, at the
expiration of that time, will be found in the place m. These
things will be so, if the bodies p and P are equally moved
in the directions of the lines pC and PC, and are therefore
urged with equal forces in those directions, but if we take an angle pCn
that is to the angle pCk as the angle VCp
to the angle VCP, and nC be equal to kC, in that
case the body p at the expiration of the time will really be
in n; and is therefore urged with a greater force than the
body P, if the angle nCp is greater than the angle
kCp, that is, if the orbit upk, move
either in consequentia or in antecedentia, with a
celerity greater than the double of that with which the line CP moves
in consequentia; and with a less force if the orbit moves
slower in antecedentia. And the difference of the forces
will be as the interval mn of the places through which the
body would be carried by the action of that difference in that given
space of time. About the centre C with the interval Cn or Ck
suppose a circle described cutting the lines mr, mn produced
in s and t, and the rectangle mn x mt
will be equal to the rectangle mk x ms, and therefore mn
will be equal to mk x ms
mt. But since the triangles pCk,
pCn, in a given time, are of a given magnitude, kr
and mr, and their difference mk, and their sum ms,
are reciprocally as the altitude pC, and therefore the
rectangle mk x ms is reciprocally as the square of the
altitude pC. But, moreover, mt is directly as ½mt,
that is, as the altitude pC. These are the first ratios of
the nascent lines: and hence mk x
ms
mt, that is, the nascent lineola mn,
and the difference of the forces proportional thereto, are
reciprocally as the cube of the altitude pC.
Q.E.D.
Cor. 1. Hence the difference of the forces in
the places P and p, or K and k, is to the force
with which a body may revolve with a circular motion from R to K, in
the same time that the body P in an immovable orb describes the arc
PK, as the nascent line mn to the versed sine of the nascent
arc RK, that is, as mk x ms
mt to rk2
2kC, or as mk x ms to the
square of rk; that is, if we take given quantities F and G
in the same ratio to one another as the angle VCP bears to the angle
VCp, as GG − FF to FF. And, therefore, if from the centre C,
with any distance CP or Cp, there be described a circular
sector equal to the whole area VPC, which the body revolving
in an immovable orbit has by a radius drawn to the centre described in
any certain time, the difference of the forces, with which the body P
revolves in an immovable orbit, and the body p in a movable
orbit, will be to the centripetal force, with which another body by a
radius drawn to the centre can uniformly describe that sector in the
same time as the area VPC is described, as GG − FF to FF. For that
sector and the area pCk are to one another as the
times in which they are described.

Cor. 2. If the orbit VPK be an ellipsis,
having its focus C, and its highest apsis V, and we suppose the the
ellipsis upk similar and equal to it, so that pC
may be always equal to PC, and the angle VCp be to the angle
VCP in the given ratio of G to F; and for the altitude PC or pC
we put A, and 2R for the latus rectum of the ellipsis, the force with
which a body may be made to revolve in a movable ellipsis will be as
FF
AA+RGG − RFF
A3, and vice versa.
Let the force with which a body may revolve in an immovable ellipsis
be expressed by the quantity FF
AA, and the force in V will be
FF
CV2. But the force with
which a body may revolve in a circle at the distance CV, with the same
velocity as a body revolving in an ellipsis has in V, is to the force
with which a body revolving in an ellipsis is acted upon in the apsis
V, as half the latus rectum of the ellipsis to the semi-diameter CV of
the circle, and therefore is as RFF
CV3; and the force which is
to this, as GG − FF to FF, is as RGG
− RFF
CV3 : and this force (by
Cor. 1 of this Prop.) is the difference of the forces in V, with which
the body P revolves in the immovable ellipsis VPK, and the body p
in the movable ellipsis upk. Therefore since by this Prop,
that difference at any other altitude A is to itself at the altitude
CV as 1
A3 to
1
CV3, the same difference
in every altitude A will be as RGG
− RFF
A3. Therefore to the force
FF
AA, by which the body may revolve in an
immovable ellipsis VPK add the excess
RGG − RFF
A3, and the sum will be the
whole force FF
AA+RGG − RFF
A3 by which a body may
revolve in the same time in the movable ellipsis upk.
Cor. 3. In the same manner it will be found,
that, if the immovable orbit VPK be an ellipsis having its centre in
the centre of the forces C, and there be supposed a movable ellipsis upk,
similar, equal, and concentrical to it; and 2R be the principal latus
rectum of that ellipsis, and 2T the latus transversum, or greater
axis; and the angle VCp be continually to the angle VCP as G
to F; the forces with which bodies may revolve in the immovable and
movable ellipsis, in equal times, will be as
FFA
T3 and
FFA
T3+RGG − RFF
A3 respectively.
Cor. 4. And universally, if the greatest
altitude CV of the body be called T, and the radius of the curvature
which the orbit VPK has in V, that is, the radius of a circle equally
curve, be called R, and the centripetal force with which a body may
revolve in any immovable trajectory VPK at the place V be called
VFF
TT, and in other places P be
indefinitely styled X; and the altitude CP be called A, and G be taken
to F in the given ratio of the angle VCp to the angle VCP;
the centripetal force with which the same body will perform the same
motions in the same time, in the same trajectory upk
revolving with a circular motion, will be as the sum of the forces
X+VRGG − VRFF
A3.
Cor. 5. Therefore the motion of a body in an immovable orbit being given, its angular motion round the centre of the forces may be increased or diminished in a given ratio; and thence new immovable orbits may be found in which bodies may revolve with new centripetal forces.
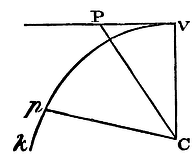
Cor. 6. Therefore if there be erected the line VP of an indeterminate length, perpendicular to the line CV given by position, and CP be drawn, and Cp equal to it, making the angle VCp having a given ratio to the angle VCP, the force with which a body may revolve in the curve line Vpk, which the point p is continually describing, will be reciprocally as the cube of the altitude Cp. For the body P, by its vis inertiae alone, no other force impelling it, will proceed uniformly in the right line VP. Add, then, a force tending to the centre C reciprocally as the cube of the altitude CP or Cp, and (by what was just demonstrated) the body will deflect from the rectilinear motion into the curve line Vpk. But this curve Vpk is the same with the curve VPQ found in Cor. 3, Prop XLI, in which, I said, bodies attracted with such forces would ascend obliquely.
Proposition xlv. Problem xxxi.
To find the motion of the apsides in orbits approaching very near to circles.
This problem is solved arithmetically by reducing the orbit, which a
body revolving in a movable ellipsis (as in Cor. 2 and 3 of the above
Prop.) describes in an immovable plane, to the figure of the orbit
whose apsides are required; and then seeking the apsides of the orbit
which that body describes in an immovable plane. But orbits acquire
the same figure. if the centripetal forces with which they are
described, compared between themselves, are made proportional at equal
altitudes. Let the point V be the highest apsis, and write T for the
greatest altitude CV, A for any other altitude CP or Cp, and
X for the difference of the altitudes CV − CP; and the force with
which a body moves in an ellipsis revolving about its focus C (as in
Cor. 2), and which in Cor. 2 was as
FF
AA +
RGG − RFF
A3, that is as,
FFA + RGG − RFF
A3,
by substituting T − X for A, will become as
RGG − RFF + TFF − FFX
A3. In like manner any other
centripetal force is to be reduced to a fraction whose denominator is
A³, and the numerators are to be made analogous by collating together
the homologous terms. This will be made plainer by Examples.
Example 1. Let us suppose the centripetal
force to be uniform, and therefore as
A3
A3 or, writing T − X for A
in the numerator, as T3
− 3TTX+3TXX − X3
A3. Then collating together
the correspondent terms of the numerators, that is, those that consist
of given quantities, with those of given quantities, and those of
quantities not given with those of quantities not given, it will
become RGG − RFF + TFF to T³ as − FFX to 3TTX + 3TXX − X³, or as −FF
to −3TT + 3TX − XX. Now since the orbit is supposed extremely near to
a circle, let it coincide with a circle; and because in that case R
and T become equal, and X is infinitely diminished, the last ratios
will be, as RGG to T², so −FF to −3TT, or as GG to TT, so FF to 3TT;
and again, as GG to FF, so TT to 3TT, that is, as 1 to 3; and
therefore G is to F, that is, the angle VCp to the angle VCP,
as 1 to √3. Therefore since the body, in an immovable
ellipsis, in descending from the upper to the lower apsis, describes an angle,
if I may so speak, of 180 deg., the other body in a movable ellipsis,
and therefore in the immovable orbit we are treating of, will in its
descent from the upper to the lower apsis, describe an angle VCp
of 180
√3 deg. And this comes to pass by reason of the likeness of
this orbit which a body acted upon by an uniform centripetal force
describes, and of that orbit which a body performing its circuits in a
revolving ellipsis will describe in a quiescent plane. By this
collation of the terms, these orbits are made similar; not
universally, indeed, but then only when they approach very near to a
circular figure. A body, therefore revolving with an uniform
centripetal force in an orbit nearly circular, will always describe an
angle of 180
√3 deg., or 103 deg., 55 m., 23 sec., at the centre; moving
from the upper apsis to the lower apsis when it has once described
that angle, and thence returning to the upper apsis when it has
described that angle again; and so on in infinitum.
Exam. 2. Suppose the centripetal force to be
as any power of the altitude A, as, for example, An−3, or
An
A3; where n − 3 and n signify
any indices of powers whatever, whether integers or fractions,
rational or surd, affirmative or negative. That numerator An
or (T − X)n being reduced to an indeterminate series by my
method of converging series, will become Tn
− nXTn−1 + nn − n
2XXTn−2, &c. And conferring these
terms with the terms of the other numerator RGG − RFF + TFF − FFX, it
becomes as RGG − RFF + TFF to Tn, so − FF to −nTn−1
+ nn − n
2XTn−2, &c. And taking the last
ratios where the orbits approach to circles, it becomes as RGG to Tn,
so − FF to −nTn−1, or as GG to Tn−1, so
FF to nTn−; and again, GG to FF, so Tn−1
to nTn−1, that is, as 1 to n; and
therefore G is to F, that is the angle VCp to the angle VCP,
as 1 to √n. Therefore since the angle VCP, described in the descent of
the body from the upper apsis to the lower apsis in an ellipsis, is of
180 deg., the angle VCp, described in the descent of the body
from the upper apsis to the lower apsis in an orbit nearly circular
which a body describes with a centripetal force proportional to the
power An−3, will be equal to an angle of
180
√n deg., and this angle being repeated, the body will return
from the lower to the upper apsis, and so on in infinitum.
As if the centripetal force be as the distance of the body from the
centre, that is, as A, or A4
A3, n will be
equal to 4, and √n equal to 2; and therefore the angle between
the upper and the lower apsis will be equal to
180
2 deg., or 90 deg. Therefore the body having performed a
fourth part of one revolution, will arrive at the lower apsis, and
having performed another fourth part, will arrive at the upper apsis,
and so on by turns in infinitum. This appears also from
Prop. X. For a body acted on by this centripetal force will revolve in
an immovable ellipsis, whose centre is the centre of force. If the
centripetal force is reciprocally as the distance, that is, directly
as 1
A or A2
A3, n will be equal to 2; and therefore
the angle between the upper and lower apsis will be
180
√2 deg., or 127 deg., 16 min., 45 sec.; and therefore a body
revolving with such a force, will by a perpetual repetition of this
angle, move alternately from the upper to the lower and from the lower
to the upper apsis for ever. So, also, if the centripetal force be
reciprocally as the biquadrate root of the eleventh power of the
altitude, that is, reciprocally as A11/4 , and, therefore,
directly as 1
A11/4 or as
A1/4
A3, n will be equal to ¼, and
180
√n deg. will be equal to 360 deg.; and therefore the body
parting from the upper apsis, and from thence perpetually descending,
will arrive at the lower apsis when it has completed one entire
revolution; and thence ascending perpetually, when it has completed
another entire revolution, it will arrive again at the upper apsis;
and so alternately for ever.
Exam. 3. Taking m and n
for any indices of the powers of the altitude, and b and c
for any given numbers, suppose the centripetal force to be as
bAm − can
A3, that is, as b
into (T − X)m + c into (T − X)n
A3 or (by the method of converging series
above-mentioned) as
bTm+cTn
− mbXTm−1ncXTn−1 +
mm − m
2bXXTm−2 + nn
− n
2cXXTn−2
A3 &c.
and comparing the terms of the numerators, there will arise RGG
− RFF + TFF to bTm + cTn as −FF
to −mbTm−1 − ncTn
+ mm − m
2bXTm−2 + nn
− n
2cXTn−2, &c. And taking the last
ratios that arise when the orbits come to a circular form, there will
come forth GG to bTm−1 + cTn−1
as FF to mbTm−1 + ncTn−1;
and again, GG to FF as bTm−1 +
cTn−1 to mbTn−1
+ ncTn−1. This proportion, by expressing
the greatest altitude CV or T arithmetically by unity, becomes, GG to
FF as b + c to mb + nc, and therefore as 1
to mb + nc
b + c. Whence G becomes to F, that is, the angle VCp
to the angle VCP, as 1 to √
mb + nc
b + c. And therefore since
the angle VCP between the upper and the lower apsis, in an immovable
ellipsis, is of 180 deg., the angle VCp between the same
apsides in an orbit which a body describes with a centripetal force,
that is, as bAm + cAn
A3, will be equal to an angle of 180
√b + c
mb + nc deg. And by the same
reasoning, if the centripetal force be as bAm
− cAn
A3, the angle between the apsides will be found
equal to 180√
b − c
mb − nc. After the same
manner the Problem is solved in more difficult cases. The quantity to
which the centripetal force is proportional must always be resolved
into a converging series whose denominator is A³. Then the given part
of the numerator arising from that operation is to be supposed in the
same ratio to that part of it which is not given, as the given part of
this numerator RGG − RFF + TFF − FFX is to
that part of the same numerator which is not given. And taking away
the superfluous quantities, and writing unity for T, the proportion of
G to F is obtained.
Cor. 1 . Hence if the centripetal force be as
any power of the altitude, that power may be found from the motion of
the apsides; and so contrariwise. That is, if the whole angular
motion, with which the body returns to the same apsis, be to the
angular motion of one revolution, or 360 deg., as any number as m
to another as n, and the altitude called A; the force will
be as the power Ann
mm−3 of the altitude
A; the index of which power is nn
mm−3. This appears by the
second example. Hence it is plain that the force in its recess from
the centre cannot decrease in a greater than a triplicate ratio of the
altitude. A body revolving with such a force and parting from the
apsis, if it once begins to descend, can never arrive at the lower
apsis or least altitude, but will descend to the centre, describing
the curve line treated of in Cor. 3, Prop. XLI. But if it should, at
its parting from the lower apsis, begin to ascend never so little, it
will ascend in infinitum, and never come to the upper apsis;
but will describe the curve line spoken of in the same Cor., and Cor.
6; Prop. XLIV. So that where the force in its recess from the centre
decreases in a greater than a triplicate ratio of the altitude, the
body at its parting from the apsis, will either descend to the centre,
or ascend in infinitum, according as it descends or ascends at the
beginning of its motion. But if the force in its recess from the
centre either decreases in a less than a triplicate ratio of the
altitude, or increases in any ratio of the altitude whatsoever, the
body will never descend to the centre, but will at some time arrive at
the lower apsis; and, on the contrary, if the body alternately
ascending and descending from one apsis to another never comes to the
centre, then either the force increases in the recess from the centre,
or it decreases in a less than a triplicate ratio of the altitude; and
the sooner the body returns from one apsis to another, the farther is
the ratio of the forces from the triplicate ratio. As if the body
should return to and from the upper apsis by an alternate descent and
ascent in 8 revolutions, or in 4, or 2, or 1½; that is, if m
should be to n as 8, or 4, or 2, or 1½ to 1, and therefore
nn
mm−3, be 1/64
− 3, or 1/16 − 3, or
1/4 − 3,
or 4/9
− 3; then the force will be as A1/64−3;
or A1/16−3;
or A1/4−3;
or A4/9−3;
that is, it will be reciprocally as A3−1/64,
or A3−1/16,
or A3−1/4,
or A3−4/9.
If the body after each revolution returns to the same apsis, and the
apsis remains unmoved, then m will be to n as 1 to
1, and therefore Ann/mm−3
will be equal to A−2, or 1/AA;
and therefore the decrease of the forces will be in a duplicate ratio
of the altitude; as was demonstrated above. If the body in three
fourth parts, or two thirds, or one third, or one fourth part of an
entire revolution, return to the same apsis; m will be to n
as ¾ or ⅔ or ⅓ or ¼ to 1, and therefore Ann/mm−3
is equal to A16/9−3,
or A9/4−3,
or A9−3, or A16−3;
and therefore the force is either reciprocally as A11/9,
or directly as A6 or A13. Lastly if the body in
its progress from the upper apsis to the same upper apsis again, goes
over one entire revolution and three deg. more, and therefore that
apsis in each revolution of the body moves three deg. in
consequentia; then m will be to n as 363
deg. to 360 deg. or as 121 to 120, and therefore Ann/mm−3
will be equal to A−29523/14641,
and therefore the centripetal force will be reciprocally as A29523/14641,
or reciprocally as A24/2 4 3
very nearly. Therefore the centripetal force decreases in a ratio
something greater than the duplicate; but approaching 59¾ times nearer
to the duplicate than the triplicate.
Cor. 2. Hence also if a body, urged by a
centripetal force which is reciprocally as the square of the altitude,
revolves in an ellipsis whose focus is in the centre of the forces;
and a new and foreign force should be added to or subducted from this
centripetal force, the motion of the apsides arising from that foreign
force may (by the third Example) be known; and so on the contrary. As
if the force with which the body revolves in the ellipsis be
as 1
AA; and the foreign force subducted
as cA, and therefore the remaining force as
A − cA4
A3; then (by the third
Example) b will be equal to 1. m equal to 1, and n
equal to 4; and therefore the angle of revolution between the apsides
is equal to 180√(1
− c
1 − 4c) deg. Suppose that
foreign force to be 357.45 parts less than the other force with which
the body revolves in the ellipsis; that is, c to be
100
35745; A or T being equal to 1; and
then 180√(1 − c
1 − 4c) will be 180√(
35645
35345) or 180.7623, that is,
180 deg., 45 min., 44 sec. Therefore the body, parting from the upper
apsis, will arrive at the lower apsis with an angular motion of 180
deg., 45 min., 44 sec, and this angular motion being repeated, will
return to the upper apsis; and therefore the upper apsis in each
revolution will go forward 1 deg., 31 min., 28 sec. The apsis of the
moon is about twice as swift.
So much for the motion of bodies in orbits whose planes pass through the centre of force. It now remains to determine those motions in eccentrical planes. For those authors who treat of the motion of heavy bodies used to consider the ascent and descent of such bodies, not only in a perpendicular direction, but at all degrees of obliquity upon any given planes; and for the same reason we are to consider in this place the motions of bodies tending to centres by means of any forces whatsoever, when those bodies move in eccentrical planes. These planes are supposed to be perfectly smooth and polished, so as not to retard the motion of the bodies in the least. Moreover, in these demonstrations, instead of the planes upon which those bodies roll or slide, and which are therefore tangent planes to the bodies, I shall use planes parallel to them, in which the centres of the bodies move, and by that motion describe orbits. And by the same method I afterwards determine the motions of bodies performed in curve superficies.