Section X.
Of the motion of bodies in given superficies, and of the reciprocal motion of funependulous bodies.
Proposition xlvi. Problem xxxii.
Any kind of centripetal force being supposed, and the centre of force, and any plane whatsoever in which the body revolves, being given, and the quadratures of curvilinear figures being allowed; it is required to determine the motion of a body going off from a given place, with a given velocity, in the direction of a given right line in that plane.
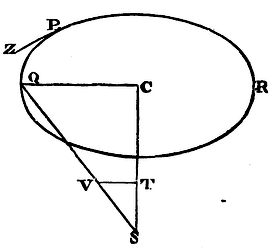
Let S be the centre of force, SC the least distance of that centre from the given plane, P a body issuing from the place P in the direction of the right line PZ, Q the same body revolving in its trajectory, and PQR the trajectory itself which is required to be found, described in that given plane. Join CQ, QS, and if in QS we take SV proportional to the centripetal force with which the body is attracted towards the centre S, and draw VT parallel to CQ, and meeting SC in T; then will the force SV be resolved into two (by Cor. 2, of the Laws of Motion), the force ST, and the force TV; of which ST attracting the body in the direction of a line perpendicular to that plane, does not at all change its motion in that plane. But the action of the other force TV, coinciding with the position of the plane itself, attracts the body directly towards the given point C in that plane; and therefore causes the body to move in this plane in the same manner as if the force ST were taken away, and the body were to revolve in free space about the centre C by means of the force TV alone. But there being given the centripetal force TV with which the body Q revolves in free space about the given centre C, there is given (by Prop. XLII) the trajectory PQR which the body describes; the place Q, in which the body will be found at any given time; and, lastly, the velocity of the body in that place Q. And so è contra. Q.E.I.
Proposition xlvii. Theorem xv.
Supposing the centripetal force to be proportional to the distance of the body from the centre; all bodies revolving in any planes whatsoever will describe ellipses, and complete their revolutions in equal times; and those which move in right lines, running backwards and forwards alternately, will complete their several periods of going and returning in the same times.
For letting all things stand as in the foregoing Proposition, the force SV, with which the body Q revolving in any plane PQR is attracted towards the centre S, is as the distance SQ; and therefore because SV and SQ, TV and CQ are proportional, the force TV with which the body is attracted towards the given point C in the plane of the orbit is as the distance CQ. Therefore the forces with which bodies found in the plane PQR are attracted towards the point C, are in proportion to the distances equal to the forces with which the same bodies are attracted every way towards the centre S; and therefore the bodies will move in the same times, and in the same figures, in any plane PQR about the point C, as they would do in free spaces about the centre S; and therefore (by Cor. 2, Prop. X, and Cor. 2, Prop. XXXVIII.) they will in equal times either describe ellipses in that plane about the centre C, or move to and fro in right lines passing through the centre C in that plane; completing the same periods of time in all cases. Q.E.D.
Scholium.
The ascent and descent of bodies in curve superficies has a near relation to these motions we have been speaking of. Imagine curve lines to be described on any plane, and to revolve about any given axes passing through the centre of force, and by that revolution to describe curve superficies; and that the bodies move in such sort that their centres may be always found in those superficies. If those bodies reciprocate to and fro with an oblique ascent and descent, their motions will be performed in planes passing through the axis, and therefore in the curve lines, by whose revolution those curve superficies were generated. In those cases, therefore, it will be sufficient to consider the motion in those curve lines.
Proposition xlviii. Theorem xvi.
If a wheel stands upon the outside of a globe at right angles thereto, and revolving about its own axis goes forward in a great circle, the length of the curvilinear path which any point, given in the perimeter of the wheel, hath described since the time that it touched the globe (which curvilinear path we may call the cycloid or epicycloid), will be to double the versed sine of half the arc which since that time has touched the globe in passing over it, as the sum of the diameters of the globe and the wheel to the semi-diameter of the globe.
Proposition xlix. Theorem xvii.
If a wheel stand upon the inside of a concave globe at right angles thereto, and revolving about its own axis go forward in one of the great circles of the globe, the length of the curvilinear path which any point, given in the perimeter of the wheel, hath described since it touched the globe, will be to the double of the versed sine of half the arc which in all that time has touched the globe in passing over it, as the difference of the diameters of the globe and the wheel to the semi-diameter of the globe.
Let ABL be the globe, C its centre, BPV the wheel insisting thereon,
E the centre of the wheel, B the point of contact, and P the given
point in the perimeter of the wheel. Imagine this wheel to proceed in
the great circle ABL from A through B towards L, and in its progress
to revolve in such a manner that the arcs AB, PB may be always equal
one to the other, and the given point P in the perimeter of the wheel
may describe in the
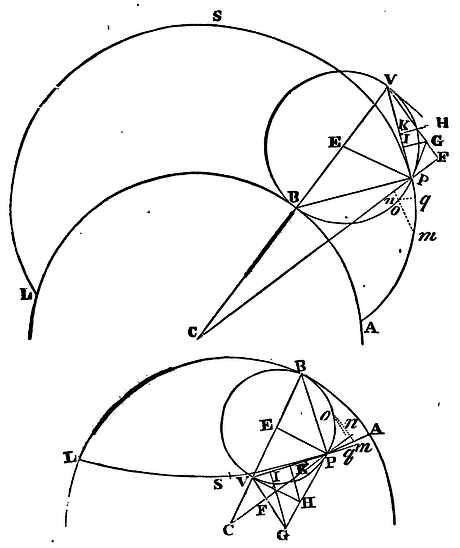 mean time the curvilinear path AP. Let AP be the whole curvilinear
path described since the wheel touched the globe in A, and the length
of this path AP will be to twice the versed sine of the arc ½PB as 2CE
to CB. For let the right line CE (produced if need be) meet the wheel
in V, and join CP, BP, EP, VP; produce CP, and let fall thereon the
perpendicular VF. Let PH, VH, meeting in H, touch the circle in P and
V, and let PH cut VF in G, and to VP let fall the perpendiculars GI,
HK. From the centre C with any interval let there be described the
circle nom, cutting the right line CP in n, the
perimeter of the wheel BP in o, and the curvilinear path AP
in m; and from the centre V with the interval Vo
let there be described a circle cutting VP produced in q.
mean time the curvilinear path AP. Let AP be the whole curvilinear
path described since the wheel touched the globe in A, and the length
of this path AP will be to twice the versed sine of the arc ½PB as 2CE
to CB. For let the right line CE (produced if need be) meet the wheel
in V, and join CP, BP, EP, VP; produce CP, and let fall thereon the
perpendicular VF. Let PH, VH, meeting in H, touch the circle in P and
V, and let PH cut VF in G, and to VP let fall the perpendiculars GI,
HK. From the centre C with any interval let there be described the
circle nom, cutting the right line CP in n, the
perimeter of the wheel BP in o, and the curvilinear path AP
in m; and from the centre V with the interval Vo
let there be described a circle cutting VP produced in q.
Because the wheel in its progress always revolves about the point of contact B, it is manifest that the right line BP is perpendicular to that curve line AP which the point P of the wheel describes, and therefore that the right line VP will touch this curve in the point P. Let the radius of the circle nom be gradually increased or diminished so that at last it become equal to the distance CP; and by reason of the similitude of the evanescent figure Pnomq, and the figure PFGVI, the ultimate ratio of the evanescent lineolae Pm, Pn, Po, Pq, that is, the ratio of the momentary mutations of the curve AP, the right line CP, the circular arc BP, and the right line VP, will be the same as of the lines PV, PF, PG, PI, respectively. But since VF is perpendicular to CF, and VH to CV, and therefore the angles HVG, VCF equal; and the angle VHG (because the angles of the quadrilateral figure HVEP are right in V and P) is equal to the angle CEP, the triangles VHG, CEP will be similar; and thence it will come to pass that as EP is to CE so is HG to HV or HP, and so KI to KP, and by composition or division as CB to CE so is PI to PK, and doubling the consequents as CB to 2CE so PI to PV, and so is Pq to Pm. Therefore the decrement of the line VP, that is, the increment of the line BV − VP to the increment of the curve line AP is in a given ratio of CB to 2CE, and therefore (by Cor. Lem. IV) the lengths BV − VP and AP, generated by those increments, are in the same ratio. But if BV be radius, VP is the cosine of the angle BVP or ½BEP, and therefore BV − VP is the versed sine of the same angle, and therefore in this wheel, whose radius is ½BV, BV − VP will be double the versed sine of the arc ½BP. Therefore AP is to double the versed sine of the arc ½BP as 2CE to CB. Q.E.D.
The line AP in the former of these Propositions we shall name the cycloid without the globe, the other in the latter Proposition the cycloid within the globe, for distinction sake.
Cor. 1. Hence if there be described the entire cycloid ASL, and the same be bisected in S, the length of the part PS will be to the length PV (which is the double of the sine of the angle VBP, when EB is radius) as 2CE to CB, and therefore in a given ratio.
Cor. 2. And the length of the semi-perimeter of the cycloid AS will be equal to a right line which is to the diameter of the wheel BV as 2CE to CB.
Proposition l. Problem xxxiii.
To cause a pendulous body to oscillate in a given cycloid.
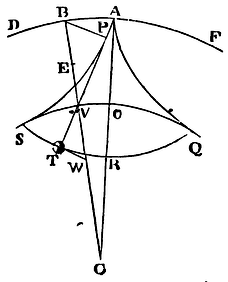
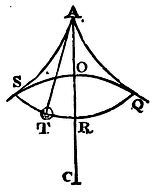
Let there be given within the globe QVS described with the centre C, the cycloid QRS, bisected in R, and meeting the superficies of the globe with its extreme points Q and S on either hand. Let there be drawn CR bisecting the arc QS in O, and let it be produced to A in such sort that CA may be to CO as CO to CR. About the centre C, with the interval CA, let there be described an exterior globe DAF; and within this globe, by a wheel whose diameter is AO, let there be described two semi-cycloids AQ, AS, touching the interior globe in Q and S, and meeting the exterior globe in A. From that point A, with a thread APT in length equal to the line AR, let the body T depend, and oscillate in such manner between the two semi-cycloids AQ, AS, that, as often as the pendulum parts from the perpendicular AR, the upper part of the thread AP may be applied to that semi-cycloid APS towards which the motion tends, and fold itself round that curve line, as if it were some solid obstacle, the remaining part of the same thread PT which has not yet touched the semi-cycloid continuing straight. Then will the weight T oscillate in the given cycloid QRS. Q.E.F.
For let the thread PT meet the cycloid QRS in T, and the circle QOS in V, and let CV be drawn; and to the rectilinear part of the thread PT from the extreme points P and T let there be erected the perpendiculars BP, TW, meeting the right line CV in B and W. It is evident, from the construction and generation of the similar figures AS, SR, that those perpendiculars PB, TW, cut off from CV the lengths VB, VW equal the diameters of the wheels OA, OR. Therefore TP is to VP (which is double the sine of the angle VBP when ½BV is radius) as BW to BV, or AO + OR to AO, that is (since CA and CO, CO and CR, and by division AO and OR are proportional), as CA + CO to CA, or, if BV be bisected in E, as 2CE to CB. Therefore (by Cor. 1, Prop. XLIX), the length of the rectilinear part of the thread PT is always equal to the arc of the cycloid PS, and the whole thread APT is always equal to the half of the cycloid APS, that is (by Cor. 2, Prop. XLIX), to the length AR. And therefore contrariwise, if the string remain always equal to the length AR, the point T will always move in the given cycloid QRS. Q.E.D.
Cor. The string AR is equal to the semi-cycloid AS, and therefore has the same ratio to AC the semi-diameter of the exterior globe as the like semi-cycloid SR has to CO the semi-diameter of the interior globe.
Proposition li. Theorem xviii.
If a centripetal force tending on all sides to the centre C of a globe, be in all places as the distance of the place from the centre, and by this force alone acting upon it, the body T oscillate (in the manner above described) in the perimeter of the cycloid QRS; I say, that all the oscillations, how unequal soever in themselves, will be performed in equal times.
For upon the tangent TW infinitely produced let fall the
perpendicular CX, and join CT. Because the centripetal force with
which the body T is impelled towards C is as the distance CT, let this
(by Cor. 2, of the Laws) be resolved into the parts CX, TX, of which
CX impelling the body directly from P stretches the thread PT, and by
the resistance the thread makes to it is totally employed, producing
no other effect; but the other part TX, impelling the body
transversely or towards X, directly accelerates the motion in the
cycloid. Then it is plain that the acceleration of the body,
proportional to this accelerating force, will be every
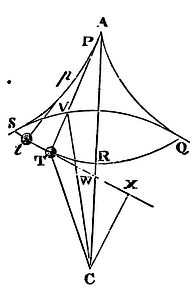 moment as the length TX, that is (because CV,
WV, and TX, TW proportional to them are given), as the length TW, that
is (by Cor. 1, Prop. XLIX) as the length of the arc of the cycloid TR.
If therefore two pendulums APT, Apt, be unequally drawn aside
from the perpendicular AR, and let fall together, their accelerations
will be always as the arcs to be described TR, tR. But the
parts described at the beginning of the motion are as the
accelerations, that is, as the wholes that are to be described at the
beginning, and therefore the parts which remain to be described, and
the subsequent accelerations proportional to those parts, are also as
the wholes, and so on. Therefore the accelerations, and consequently
the velocities generated, and the parts described with those
velocities; and the parts to be described, are always as the wholes;
and therefore the parts to be described preserving a given ratio to
each other will vanish together, that is, the two bodies oscillating
will arrive together at the perpendicular AR. And since on the other
hand the ascent of the pendulums from the lowest place R through the
same cycloidal arcs with a retrograde motion, is retarded in the
several places they pass through by the same forces by which their
descent was accelerated; it is plain that the velocities of their
ascent and descent through the same arcs are equal, and consequently
performed in equal times; and, therefore, since the two parts of the
cycloid RS and RQ lying on either side of the perpendicular are
similar and equal, the two pendulums will perform as well the wholes
as the halves of their oscillations in the same times.
Q.E.D.
moment as the length TX, that is (because CV,
WV, and TX, TW proportional to them are given), as the length TW, that
is (by Cor. 1, Prop. XLIX) as the length of the arc of the cycloid TR.
If therefore two pendulums APT, Apt, be unequally drawn aside
from the perpendicular AR, and let fall together, their accelerations
will be always as the arcs to be described TR, tR. But the
parts described at the beginning of the motion are as the
accelerations, that is, as the wholes that are to be described at the
beginning, and therefore the parts which remain to be described, and
the subsequent accelerations proportional to those parts, are also as
the wholes, and so on. Therefore the accelerations, and consequently
the velocities generated, and the parts described with those
velocities; and the parts to be described, are always as the wholes;
and therefore the parts to be described preserving a given ratio to
each other will vanish together, that is, the two bodies oscillating
will arrive together at the perpendicular AR. And since on the other
hand the ascent of the pendulums from the lowest place R through the
same cycloidal arcs with a retrograde motion, is retarded in the
several places they pass through by the same forces by which their
descent was accelerated; it is plain that the velocities of their
ascent and descent through the same arcs are equal, and consequently
performed in equal times; and, therefore, since the two parts of the
cycloid RS and RQ lying on either side of the perpendicular are
similar and equal, the two pendulums will perform as well the wholes
as the halves of their oscillations in the same times.
Q.E.D.
Cor. The force with which the body T is accelerated or retarded in any place T of the cycloid, is to the whole weight of the same body in the highest place S or Q as the arc of the cycloid TR is to the arc SR or QR.
Proposition lii. Problem xxxiv.
To define the velocities of the pendulums in the several places, and the times in which both the entire oscillations, and the several parts of them are performed.
About any centre G, with the interval GH equal to the arc of the
cycloid RS, describe a semi-circle HKM bisected by the semi-diameter
GK. And if a centripetal force proportional to the distance of the
places from the centre tend to the centre G, and it be in the
perimeter HIK equal to the centripetal force in the perimeter of the
globe QOS tending towards its centre, and at the same time that the
pendulum T is let fall from the highest place S, a body, as L, is let
fall from H to G; then because the
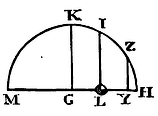 forces which act upon the bodies are equal at the beginning, and
always proportional to the spaces to be described TR, LG, and
therefore if TR and LG are equal, are also equal in the places T and
L, it is plain that those bodies describe at the beginning equal
spaces ST, HL, and therefore are still acted upon equally, and
continue to describe equal spaces. Therefore by Prop. XXXVIII, the
time in which the body describes the arc ST is to the time of one
oscillation, as the arc HI the time in which the body H arrives at L,
to the semi-periphery HKM, the time in which the body H will come to
M. And the velocity of the pendulous body in the place T is to its
velocity in the lowest place R, that is, the velocity of the body H in
the place L to its velocity in the place G; or the momentary increment
of the line HL to the momentary increment of the line HG (the arcs HI,
HK increasing with an equable flux) as the ordinate LI to the radius
GK, or as √(SR2 − TR2)
to SR. Hence, since in unequal oscillations there are described in
equal time arcs proportional to the entire arcs of the oscillations,
there are obtained from the times given, both the velocities and the
arcs described in all the oscillations universally. Which was first
required.
forces which act upon the bodies are equal at the beginning, and
always proportional to the spaces to be described TR, LG, and
therefore if TR and LG are equal, are also equal in the places T and
L, it is plain that those bodies describe at the beginning equal
spaces ST, HL, and therefore are still acted upon equally, and
continue to describe equal spaces. Therefore by Prop. XXXVIII, the
time in which the body describes the arc ST is to the time of one
oscillation, as the arc HI the time in which the body H arrives at L,
to the semi-periphery HKM, the time in which the body H will come to
M. And the velocity of the pendulous body in the place T is to its
velocity in the lowest place R, that is, the velocity of the body H in
the place L to its velocity in the place G; or the momentary increment
of the line HL to the momentary increment of the line HG (the arcs HI,
HK increasing with an equable flux) as the ordinate LI to the radius
GK, or as √(SR2 − TR2)
to SR. Hence, since in unequal oscillations there are described in
equal time arcs proportional to the entire arcs of the oscillations,
there are obtained from the times given, both the velocities and the
arcs described in all the oscillations universally. Which was first
required.
Let now any pendulous bodies oscillate in different cycloids
described within different globes, whose absolute forces are also
different; and if the absolute force of any globe QOS be called V, the
accelerative force with which the pendulum is acted on in the
circumference of this globe, when it begins to move directly towards
its centre, will be as the distance of the pendulous body from that
centre and the absolute force of the globe conjunctly, that is, as CO
x V. Therefore the lineola HY, which is as this accelerated force CO x
V, will be described in a given time; and if there be erected the
perpendicular YZ meeting the circumference in Z, the nascent arc HZ
will denote that given time. But that nascent arc HZ is in the
subduplicate ratio of the rectangle GHY, and therefore as √(GH
x CO x V). Whence the time of an entire oscillation in the
cycloid QRS (it being as the semi-periphery HKM, which denotes that
entire oscillation, directly; and as the arc HZ which in like manner
denotes a given time inversely) will be as GH directly and √(GH
x CO x V) inversely; that is, because GH and SR are equal, as
√(SR
CO x V), or (by Cor. Prop.
L,) as √(AR
AC x V). Therefore the
oscillations in all globes and cycloids, performed with what absolute
forces soever, are in a ratio compounded of the subduplicate ratio of
the length of the string directly, and the subduplicate ratio of the
distance between the point of suspension and the centre of the globe
inversely, and the subduplicate ratio of the absolute force of the
globe inversely also. Q.E.I.
Cor. 1. Hence also
the times of oscillating, falling, and revolving bodies may be
compared among themselves. For if the diameter of the wheel with which
the cycloid is described within the globe is supposed equal to the
semi-diameter of the globe, the cycloid will become a right line
passing through the centre of the globe, and the oscillation will be
changed into a descent and subsequent ascent in that right line.
Whence there is given both the time of the descent from any place to
the centre, and the time equal to it in which the body revolving
uniformly about the centre of the globe at any distance describes an
arc of a quadrant. For this time (by Case 2) is to the time of half
the oscillation in any cycloid QRS as 1 to √(
AR
AC).
Cor. 2. Hence also follow what Sir Christopher Wren and M. Huygens have discovered concerning the vulgar cycloid. For if the diameter of the globe be infinitely increased, its sphaerical superficies will be changed into a plane, and the centripetal force will act uniformly in the direction of lines perpendicular to that plane, and this cycloid of our's will become the same with the common cycloid. But in that case the length of the arc of the cycloid between that plane and the describing point will become equal to four times the versed sine of half the arc of the wheel between the same plane and the describing point, as was discovered by Sir Christopher Wren. And a pendulum between two such cycloids will oscillate in a similar and equal cycloid in equal times, as M. Huygens demonstrated. The descent of heavy bodies also in the time of one oscillation will be the same as M. Huygens exhibited.
The propositions here demonstrated are adapted to the true constitution of the Earth, in so far as wheels moving in any of its great circles will describe, by the motions of nails fixed in their perimeters, cycloids without the globe; and pendulums, in mines and deep caverns of the Earth, must oscillate in cycloids within the globe, that those oscillations may be performed in equal times. For gravity (as will be shewn in the third book) decreases in its progress from the superficies of the Earth; upwards in a duplicate ratio of the distances from the centre of the Earth; downwards in a simple ratio of the same.
Proposition liii. Problem xxxv.
Granting the quadratures of curvilinear figures, it is required to find the forces with which bodies moving in given curve lines may always perform their oscillations in equal times.
Let the body T oscillate in any curve line STRQ, whose axis is AR
passing through the centre of force C. Draw TX touching that curve in
any place of the body T, and in that tangent TX take TY equal to the
arc TR. The length of that arc is known from the common methods used
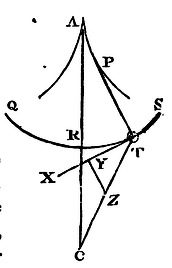 for the quadratures of figures.
From the point Y draw the right line YZ perpendicular to the tangent.
Draw CT meeting that perpendicular in Z, and the centripetal force
will be proportional to the right line TZ. Q.E.I.
for the quadratures of figures.
From the point Y draw the right line YZ perpendicular to the tangent.
Draw CT meeting that perpendicular in Z, and the centripetal force
will be proportional to the right line TZ. Q.E.I.
For if the force with which the body is attracted from T towards C be expressed by the right line TZ taken proportional to it, that force will be resolved into two forces TY, YZ, of which YZ drawing the body in the direction of the length of the thread PT, does not at all change its motion; whereas the other force TY directly accelerates or retards its motion in the curve STRQ. Wherefore since that force is as the space to be described TR, the accelerations or retardations of the body in describing two proportional parts (a greater and a less) of two oscillations, will be always as those parts, and therefore will cause those parts to be described together. But bodies which continually describe together parts proportional to the wholes, will describe the wholes together also. Q.E.D.
Cor. 1. Hence if the body T, hanging by a rectilinear thread AT from the centre A, describe the circular arc STRQ, and in the mean time be acted on by any force tending downwards with parallel directions, which is to the uniform force of gravity as the arc TR to its sine TN, the times of the several oscillations will be equal. For because TZ, AR are parallel, the triangles ATN, ZTY are similar; and therefore TZ will be to AT as TY to TN; that is, if the uniform force of gravity be expressed by the given length AT, the force TZ, by which the oscillations become isochronous, will be to the force of gravity AT, as the arc TR equal to TY is to TN the sine of that arc.
Cor. 2. And therefore in clocks, if forces were impressed by some machine upon the pendulum which preserves the motion, and so compounded with the force of gravity that the whole force tending downwards should be always as a line produced by applying the rectangle under the arc TR and the radius AR to the sine TN, all the oscillations will become isochronous.
Proposition liv. Problem xxxvi.
Granting the quadratures of curvilinear figures, it is required to find the times in which bodies by means of any centripetal force will descend or ascend in any curve lines described in a plane passing through the centre of force.
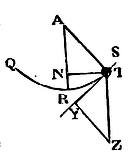
Let the body descend from any place S, and move in any curve STtR
given in a plane passing through the centre of force C. Join CS, and let
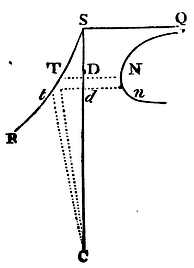 it be divided into innumerable equal parts, and let Dd be one of
those parts. From the centre C, with the intervals CD, Cd,
let the circles DT, dt be described, meeting the curve line
STtR in T and t. And because the law of centripetal
force is given, and also the altitude CS from which the body at first
fell, there will be given the velocity of the body in any other
altitude CT (by Prop. XXXIX). But the time in which the body describes
the lineola Tt is as the length of that lineola, that is, as
the secant of the angle tTC directly, and the velocity
inversely. Let the ordinate DN, proportional to this time, be made
perpendicular to the right line CS at the point D, and because Dd
is given, the rectangle Dd x DN, that is, the area DNnd,
will be proportional to the same time. Therefore if PNn be a
curve line in which the point N is perpetually found, and its
asymptote be the right line SQ standing upon the line CS at right
angles, the area SQPND will be proportional to the time in which the
body in its descent hath described the line ST; and therefore that
area being found, the time is also given. Q.E.I.
it be divided into innumerable equal parts, and let Dd be one of
those parts. From the centre C, with the intervals CD, Cd,
let the circles DT, dt be described, meeting the curve line
STtR in T and t. And because the law of centripetal
force is given, and also the altitude CS from which the body at first
fell, there will be given the velocity of the body in any other
altitude CT (by Prop. XXXIX). But the time in which the body describes
the lineola Tt is as the length of that lineola, that is, as
the secant of the angle tTC directly, and the velocity
inversely. Let the ordinate DN, proportional to this time, be made
perpendicular to the right line CS at the point D, and because Dd
is given, the rectangle Dd x DN, that is, the area DNnd,
will be proportional to the same time. Therefore if PNn be a
curve line in which the point N is perpetually found, and its
asymptote be the right line SQ standing upon the line CS at right
angles, the area SQPND will be proportional to the time in which the
body in its descent hath described the line ST; and therefore that
area being found, the time is also given. Q.E.I.
Proposition lv. Theorem xix.
If a body move in any curve superficies, whose axis passes through the centre of force, and from the body a perpendicular be let fall upon the axis; and a line parallel and equal thereto be drawn from any given point of the axis; I say, that this parallel line will describe an area proportional to the time.
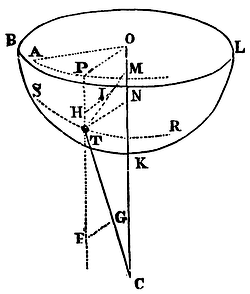
Let BKL be a curve superficies, T a body revolving in it, STR a trajectory which the body describes in the same, S the beginning of the trajectory, OMK the axis of the curve superficies, TN a right line let fall perpendicularly from the body to the axis; OP a line parallel and equal thereto drawn from the given point O in the axis; AP the orthographic projection of the trajectory described by the point P in the plane AOP in which the revolving line OP is found; A the beginning of that projection, answering to the point S; TC a right line drawn from the body to the centre; TG a part thereof proportional to the centripetal force with which the body tends towards the centre C; TM a right line perpendicular to the curve superficies; TI a part thereof proportional to the force of pressure with which the body urges the superficies, and therefore with which it is again repelled by the superficies towards M; PTF a right line parallel to the axis and passing through the body, and GF, IH right lines let fall perpendicularly from the points G and I upon that parallel PHTF. I say, now. that the area AOP, described by the radius OP from the beginning of the motion, is proportional to the time. For the force TG (by Cor. 2, of the Laws of Motion) is resolved into the forces TF, FG; and the force TI into the forces TH, HI; but the forces TF, TH, acting in the direction of the line PF perpendicular to the plane AOP, introduce no change in the motion of the body but in a direction perpendicular to that plane. Therefore its motion, so far as it has the same direction with the position of the plane, that is, the motion of the point P, by which the projection AP of the trajectory is described in that plane, is the same as if the forces TF, TH were taken away, and the body were acted on by the forces FG, HI alone; that is, the same as if the body were to describe in the plane AOP the curve AP by means of a centripetal force tending to the centre O, and equal to the sum of the forces FG and HI. But with such a force as that (by Prop. 1) the area AOP will be described proportional to the time. Q.E.D.
Cor. By the same reasoning, if a body, acted on by forces tending to two or more centres in any the same right line CO, should describe in a free space any curve line ST, the area AOP would be always proportional to the time.
Proposition lvi. Problem xxxvii.
Granting the quadratures of curvilinear figures, and supposing that there are given both the law of centripetal force tending to a given centre, and the curve superficies whose axis passes through that centre; it is required to find the trajectory which a body will describe in that superficies, when going off from a given place with a given velocity, and in a given direction in that superficies.
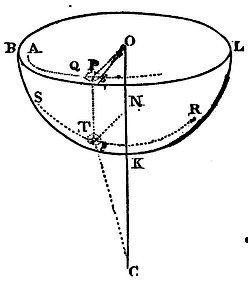
The last construction remaining, let the body T go from the given place S, in the direction of a line given by position, and turn into the trajectory sought STR, whose orthographic projection in the plane BDO is AP. And from the given velocity of the body in the altitude SC, its velocity in any other altitude TC will be also given. With that velocity, in a given moment of time, let the body describe the particle Tt of its trajectory, and let Pp be the projection of that particle described in the plane AOP. Join Op, and a little circle being described upon the curve superficies about the centre T with the interval Tt let the projection of that little circle in the plane AOP be the ellipsis pQ. And because the magnitude of that little circle Tt, and TN or PO its distance from the axis CO is also given, the ellipsis pQ will be given both in kind and magnitude, as also its position to the right line PO. And since the area POp is proportional to the time, and therefore given because the time is given, the angle POp will be given. And thence will be given p the common intersection of the ellipsis and the right line Op, together with the angle OPp, in which the projection APp of the trajectory cuts the line OP. But from thence (by conferring Prop. XLI, with its 2d Cor.) the manner of determining the curve APp easily appears. Then from the several points P of that projection erecting to the plane AOP, the perpendiculars PT meeting the curve superficies in T, there will be given the several points T of the trajectory. Q.E.I.