Section viii.
Of the invention of orbits wherein bodies will revolve, being acted upon by any sort of centripetal force.
Proposition xl. Theorem xiii.
If a body, acted upon by any centripetal force, is any how moved, and another body ascends or descends in a right line, and their velocities be equal in any one case of equal altitudes, their velocities will be also equal at all equal altitudes.
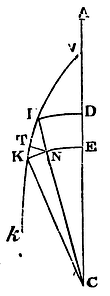
Let a body descend from A through D and E, to the centre C; and let another body move from V in the curve line VIKk. From the centre C, with any distances, describe the concentric circles DI, EK, meeting the right line AC in D and E, and the curve VIK in I and K. Draw IC meeting KE in N, and on IK let fall the perpendicular NT; and let the interval DE or IN between the circumferences of the circles be very small; and imagine the bodies in D and I to have equal velocities. Then because the distances CD and CI are equal, the centripetal forces in D and I will be also equal. Let those forces be expressed by the equal lineolae DE and IN; and let the force IN (by Cor. 2 of the Laws of Motion) be resolved into two others, NT and IT. Then the force NT acting in the direction of the line NT perpendicular to the path ITK of the body will not at all affect or change the velocity of the body in that path, but only draw it aside from a rectilinear course, and make it deflect perpetually from the tangent of the orbit, and proceed in the curvilinear path ITKk. That whole force, therefore, will be spent in producing this effect; but the other force IT, acting in the direction of the course of the body, will be all employed in accelerating it, and in the least given time will produce an acceleration proportional to itself. Therefore the accelerations of the bodies in D and I, produced in equal times, are as the lines DE, IT (if we take the first ratios of the nascent lines DE, IN, IK, IT, NT); and in unequal times as those lines and the times conjunctly. But the times in which DE and IK are described, are, by reason of the equal velocities (in D and I) as the spaces described DE and IK, and therefore the accelerations in the course of the bodies through the lines DE and IK are as DE and IT, and DE and IK conjunctly; that is, as the square of DE to the rectangle IT into IK. But the rectangle IT x IK is equal to the square of IN, that is, equal to the square of DE; and therefore the accelerations generated in the passage of the bodies from D and I to E and K are equal. Therefore the velocities of the bodies in E and K are also equal, and by the same reasoning they will always be found equal in any subsequent equal distances. Q.E.D.
By the same reasoning, bodies of equal velocities and equal distances from the centre will he equally retarded in their ascent to equal distances. Q.E.D.
Cor. 1. Therefore if a body either oscillates by hanging to a string, or by any polished and perfectly smooth impediment is forced to move in a curve line; and another body ascends or descends in a right line, and their velocities be equal at any one equal altitude, their velocities will be also equal at all other equal altitudes. For by the string of the pendulous body, or by the impediment of a vessel perfectly smooth, the same thing will be effected as by the transverse force NT. The body is neither accelerated nor retarded by it, but only is obliged to leave its rectilinear course.
Cor. 2. Suppose the quantity P to be the greatest distance from the centre to which a body can ascend, whether it be oscillating, or revolving in a trajectory, and so the same projected upwards from any point of a trajectory with the velocity it has in that point. Let the quantity A be the distance of the body from the centre in any other point of the orbit; and let the centripetal force be always as the power An−1, of the quantity A, the index of which power n−1 is any number n diminished by unity. Then the velocity in every altitude A will be as √(Pa − An) and therefore will be given. For by Prop. XXXIX, the velocity of a body ascending and descending in a right line is in that very ratio.
Proposition xli. Problem xxviii.
Supposing a centripetal force of any kind, and granting the quadratures of curvilinear figures, it is required to find as well the trajectories in which bodies will move, as the times of their motions in the trajectories found.
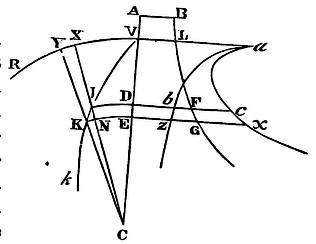
Let any centripetal force tend to the centre C, and let it be
required to find the trajectory VIKk. Let there be given the
circle VR, described from the centre C with any interval CV; and from
the same centre describe any other circles ID, KE cutting the
trajectory in I and K, and the right line CV in D and E. Then draw the
right line CNIX cutting the circles KE, VR in N and X, and the right
line CKY meeting the circle VR in Y. Let the points I and K be
indefinitely near; and let the body go on from V through I and K to k;
and let the point A be the place from whence another body is to fall,
so as in the place D to acquire a velocity equal to the velocity of
the first body in I. And things remaining as in Prop. XXXIX, the
lineola IK, described in the least given time will
be as the velocity, and therefore as the right line whose square is
equal to the area ABFD, and the triangle ICK proportional to the time
will be given, and therefore KN will be reciprocally as the altitude
IC; that is (if there be given any quantity Q, and the altitude IC be
called A), as Q
A. This quantity
Q
A call Z, and suppose the magnitude of
Q to be such that in some case √(ABFD) may
be to Z as IK to KN, and then in all cases √(ABFD)
will be to Z as IK to KN, and ABFD to ZZ as IK² to KN², and by
division ABFD − ZZ to ZZ as IN² to KN², and therefore √(ABFD
− ZZ) to Z; or Q
A as IN to KN; and therefore A x KN
will be equal to Q x IN
√(ABFD − ZZ). Therefore since YX x XC
is to A x KN as CX², to AA, the rectangle XY x XC will be equal to
Q x IN x CX2
AA√(ABFD − ZZ). Therefore in the
perpendicular DF let there be taken continually Db, Dc
equal to Q
2√(ABFD − ZZ),
Q x CX2
2AA√(ABFD − ZZ) respectively, and let
the curve lines ab, ac, the foci of the points b
and c, be described: and from the point V let the
perpendicular Va be erected to the line AC, cutting off the
curvilinear areas VDba, VDca, and let the ordinates
Ez, Ex, be erected also. Then because the rectangle
Db x IN or DbzE is equal to half the rectangle A x
KN, or to the triangle ICK; and the rectangle Dc x IN or DcxE
is equal to half the rectangle YX x XC, or to the triangle XCY; that
is, because the nascent particles DbzE, ICK of the areas VDba,
VIC are always equal; and the nascent particles DcxE, XCY of
the areas VDca, VCX are always equal: therefore the generated
area VDba will be equal to the generated area VIC, and
therefore proportional to the time; and the generated area VDca
is equal to the generated sector VCX. If, therefore, any time be given
during which the body has been moving from V, there will be also given
the area proportional to it VDba; and thence will be given
the altitude of the body CD or CI; and the area VDca, and the
sector VCX equal thereto, together with its angle VCI. But the angle
VCI, and the altitude CI being given, there is also given the place I,
in which the body will be found at the end of that time.
Q.E.I.
Cor. 1. Hence the greatest and least altitudes of the bodies, that is, the apsides of the trajectories, may be found very readily. For the apsides are those points in which a right line IC drawn through the centre falls perpendicularly upon the trajectory VIK; which comes to pass when the right lines IK and NK become equal; that is, when the area ABFD is equal to ZZ.
Cor. 2. So also the angle KIN, in which the trajectory at any place cuts the line IC, may be readily found by the given altitude IC of the body: to wit, by making the sine of that angle to radius as KN to IK that is, as Z to the square root of the area ABFD.
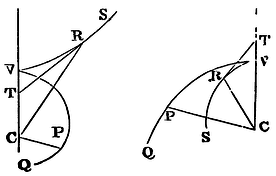
Cor. 3. If to the centre C, and the principal vertex V, there be described a conic section VRS; and from any point thereof, as R, there be drawn the tangent RT meeting the axis CV indefinitely produced in the point T; and then joining CR there be drawn the right line CP, equal to the abscissa CT, making an angle VCP proportional to the sector VCR; and if a centripetal force, reciprocally proportional to the cubes of the distances of the places from the centre, tends to the centre C; and from the place V there sets out a body with a just velocity in the direction of a line perpendicular to the right line CV; that body will proceed in a trajectory VPQ, which the point P will always touch; and therefore if the conic section VRS be an hyberbola, the body will descend to the centre; but if it be an ellipsis, it will ascend perpetually, and go farther and farther off in infinitum. And, on the contrary, if a body endued with any velocity goes off from the place V, and according as it begins either to descend obliquely to the centre, or ascends obliquely from it, the figure VRS be either an hyperbola or an ellipsis, the trajectory may be found by increasing or diminishing the angle VCP in a given ratio. And the centripetal force becoming centrifugal, the body will ascend obliquely in the trajectory VPQ, which is found by taking the angle VCP proportional to the elliptic sector VRC, and the length CP equal to the length CT, as before. All these things follow from the foregoing Proposition, by the quadrature of a certain curve, the invention of which, as being easy enough, for brevity's sake I omit.
Proposition xlii. Problem xxix.
The law of centripetal force being given, it is required to find the motion of a body setting out from a given place, with a given velocity, in the direction of a given right line.
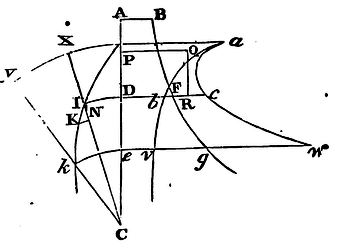
Suppose the same things as in the three preceding propositions; and let the body go off from the place I in the direction of the little line, IK, with the same velocity as another body, by falling with an uniform centripetal force from the place P, may acquire in D; and let this uniform force be to the force with which the body is at first urged in I, as DR to DF. Let the body go on towards k; and about the centre C, with the interval Ck, describe the circle ke, meeting the right line PD in e, and let there be erected the lines eg, ev, ew, ordinately applied to the curves BFg, abv, acw. From the given rectangle PDRQ and the given law of centripetal force, by which the first body is acted on, the curve line BFg is also given, by the construction of Prop. XXVII, and its Cor. 1. Then from the given angle CIK is given the proportion of the nascent lines IK, KN; and thence, by the construction of Prob. XXVIII, there is given the quantity Q, with the curve lines abv, acw; and therefore, at the end of any time Dbve, there is given both the altitude of the body Ce or Ck, and the area Dcwe, with the sector equal to it XCy, the angle ICk, and the place k, in which the body will then be found. Q.E.I.
We suppose in these Propositions the centripetal force to vary in its recess from the centre according to some law, which any one may imagine at pleasure; but at equal distances from the centre to be everywhere the same.
I have hitherto considered the motions of bodies in immovable orbits. It remains now to add something concerning their motions in orbits which revolve round the centres of force.