Section vii.
Concerning the rectilinear ascent and descent of bodies.
Proposition xxxii. Problem xxiv.
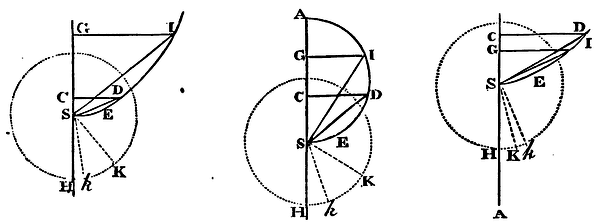
Supposing that the centripetal force is reciprocally proportional to the square of the distance of the places from the centre; it is required to define the spaces which a body, falling directly, describes in given times.
Case 1. If the body does not fall
perpendicularly, it will (by Cor. 1
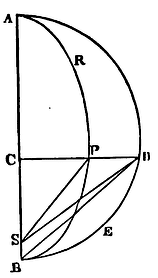 Prop. XIII) describe some conic section whose focus is A placed in the
centre of force. Suppose that conic section to be ARPB and its focus
S. And, first, if the figure be an ellipsis, upon the greater axis
thereof AB describe the semi-circle ADB, and let the right line DPC
pass through the falling body, making right angles with the axis; and
drawing DS, PS, the area ASD will be proportional to the area ASP, and
therefore also to the time. The axis AB still remaining the same, let
the breadth of the ellipsis be perpetually diminished, and the area
ASD will always remain proportional to the time. Suppose that breadth
to be diminished in infinitum; and the orbit APB in that
case coinciding with the axis AB, and the focus S with the extreme
point of the axis B, the body will descend in the right line AC, and
the area ABD will become proportional to the time. Wherefore the space
AC will be given which the body describes in a given time by its
perpendicular fall from the place A, if the area ABD is taken
proportional to the time, and from the point D the right line DC is
let fall perpendicularly on the right line AB. Q.E.I.
Prop. XIII) describe some conic section whose focus is A placed in the
centre of force. Suppose that conic section to be ARPB and its focus
S. And, first, if the figure be an ellipsis, upon the greater axis
thereof AB describe the semi-circle ADB, and let the right line DPC
pass through the falling body, making right angles with the axis; and
drawing DS, PS, the area ASD will be proportional to the area ASP, and
therefore also to the time. The axis AB still remaining the same, let
the breadth of the ellipsis be perpetually diminished, and the area
ASD will always remain proportional to the time. Suppose that breadth
to be diminished in infinitum; and the orbit APB in that
case coinciding with the axis AB, and the focus S with the extreme
point of the axis B, the body will descend in the right line AC, and
the area ABD will become proportional to the time. Wherefore the space
AC will be given which the body describes in a given time by its
perpendicular fall from the place A, if the area ABD is taken
proportional to the time, and from the point D the right line DC is
let fall perpendicularly on the right line AB. Q.E.I.
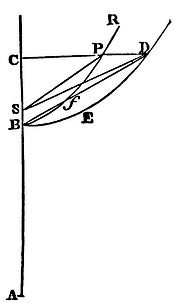
Case 2. If the figure RPB is an hyperbola, on the same principal diameter AB describe the rectangular hyperbola BED; and because the areas CSP, CBfP, SPfB, are severally to the several areas CSD, CBED, SDEB, in the given ratio of the heights CP, CD, and the area SPfB is proportional to the time in which the body P will move through the arc PfB. the area SDEB will be also proportional to that time. Let the latus rectum of the hyperbola RPB be diminished in infinitum, the latus transversum remaining the same; and the arc PB will come to coincide with the right line CB, and the focus S, with the vertex B, and the right line SD with the right line BD. And therefore the area BDEB will be proportional to the time in which the body C, by its perpendicular descent, describes the line CB. Q.E.I.
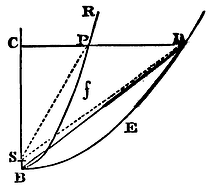
Case 3. And by the like argument, if the figure RPB is a parabola, and to the same principal vertex B another parabola BED is described, that may always remain given while the former para bola in whose perimeter the body P moves, by having its latus rectum diminished and reduced to nothing, comes to coincide with the line CB, the parabolic segment BDEB will be proportional to the time in which that body P or C will descend to the centre S or B. Q.E.I
Proposition xxxiii. Theorem ix.
The things above found being supposed. I say, that the velocity of a falling body in any place C is to the velocity of a body, describing a circle about the centre B at the distance BC, in the subduplicate ratio of AC, the distance of the body from the remoter vertex A of the circle or rectangular hyperbola, to ½AB, the principal semi-diameter of the figure.
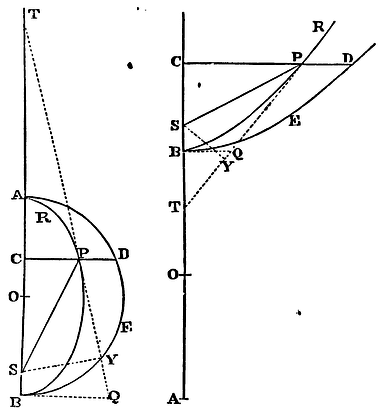
Let AB, the common diameter of both figures RPB, DEB, be bisected in
O; and draw the right line PT that may touch the figure RPB in P, and
likewise cut that common diameter AB (produced, if need be) in T; and
let SY be perpendicular to this line, and BQ to this diameter, and
suppose the latus rectum of the figure RPB to be L. From Cor. 9, Prop.
XVI, it is manifest that the velocity of a body, moving in the line
RPB about the centre S, in any place P, is to the velocity of a body
describing a circle about the same centre, at the distance SP, in the
subduplicate ratio of the rectangle ½L x SP to SY². For by the
properties of the conic sections ACB is to CP² as 2AO to L, and
therefore 2CP2 x AO
ACB is equal to L. Therefore those
velocities are to each other in the subduplicate ratio of
CP2 x AO x SP
ACB to SY². Moreover, by the properties
of the conic sections, CO is to BO as BO to TO, and (by composition or
division) as CB to BT. Whence (by division or composition) BO − or +
CO will be to BO as CT to BT, that is, AC will be to AO as CP to BQ;
and therefore CP2 x AO
x SP
ACB is equal to
BQ2 x AC x SP
AO x BC. Now suppose CP, the breadth of
the figure RPB, to be diminished in infinitum, so as the
point P may come to coincide with the point C, and the point S with
the point B, and the line SP with the line BC, and the line SY with
the line BQ; and the velocity of the body now descending
perpendicularly in the line CB will be to the velocity of a
body describing a circle about the centre B, at the distance BC; in
the subduplicate ratio of BQ2
x AC x SP
AO x BC to SY², that is (neglecting the
ratios of equality of SP to BC, and BQ² to SY²), in the subduplicate
ratio of AC to AO, or ½AB. Q.E.D.
Cor. 1. When the points B and S come to coincide, TC will become to TS as AC to AO.
Cor. 2. A body revolving in any circle at a given distance from the Centre, by its motion converted upwards, will ascend to double its distance from the centre.
Proposition xxxiv. Theorem X.
If the figure BED is a parabola, I say, that the velocity of a falling body in any place C is equal to the velocity by which a body may uniformly describe a circle about the centre B at half the interval BC.
For (by Cor. 7, Prop. XVI) the velocity of a body describing a parabola RPB about the centre S, in any place P, is equal to the velocity of a body uniformly describing a circle about the same centre S at half the interval SP. Let the breadth CP of the parabola be diminished in infinitum, so as the parabolic arc PfB may come to coincide with the right line CB, the centre S with the vertex B, and the interval SP with the interval BC, and the proposition will be manifest. Q.E.D.
Proposition xxxv. Theorem xi.
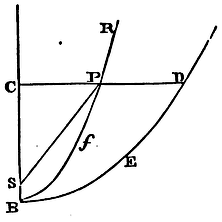
The same things supposed, I say, that the area of the figure DES, described by the indefinite radius SD, is equal to the area which a body with a radius equal to half the latus rectum of the figure DES, by uniformly revolving about the centre S, may describe in the same time.
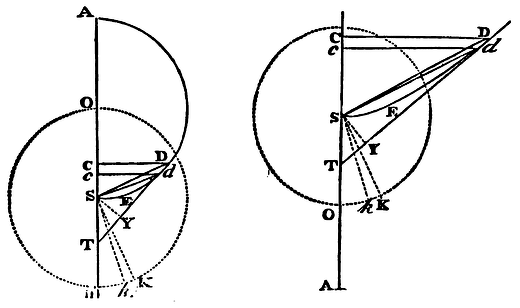
For suppose a body C in the smallest moment of time describes in falling the infinitely little line Cc, while another body K, uniformly revolving about the centre S in the circle OKk, describes the arc Kk. Erect the perpendiculars CD, cd, meeting the figure DES in D, d. Join SD, Sd, SK, Sk, and draw Dd meeting the axis AS in T, and thereon let fall the perpendicular SY.
Case 1. If the figure DES is a circle, or a rectangular hyperbola, bisect its transverse diameter AS in O, and SO will be half the latus rectum. And because TC is to TD as Cc to Dd, and TD to TS as CD to SY; ex aequo TC will be to TS as CD x Cc to SY x Dd. But (by Cor. 1, Prop. XXXIII) TC is to TS as AC to AO; to wit, if in the coalescence of the points D, d, the ultimate ratios of the lines are taken. Wherefore AC is to AO or SK as CD x Cc to SY x Dd. Farther, the velocity of the descending body in C is to the velocity of a body describing a circle about the centre S, at the interval SC, in the subduplicate ratio of AC to AO or SK (by Prop. XXXIII); and this velocity is to the velocity of a body describing the circle OKk in the subduplicate ratio of SK to SC (by Cor. 6, Prop IV); and, ex aequo, the first velocity to the last, that is, the little line Cc to the arc Kk, in the subduplicate ratio of AC to SC, that is, in the ratio of AC to CD. Wherefore CD x Cc is equal to AC x Kk, and consequently AC to SK as AC x Kk to SY x Dd, and thence SK x Kk equal to SY x Dd, and ½SK x Kk equal to ½SY x Dd, that is, the area KSk equal to the area SDd. Therefore in every moment of time two equal particles, KSk and SDd, of areas are generated, which, if their magnitude is diminished, and their number increased in infinitum, obtain the ratio of equality, and consequently (by Cor. Lem. IV), the whole areas together generated are always equal. Q.E.D.
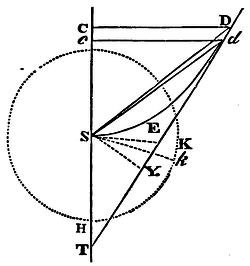
Case 2. But if the figure DES is a parabola, we shall find, as above, CD x Cc to SY x Dd as TC to TS, that is, as 2 to 1; and that therefore ¼CD x Cc is equal to ½SY x Dd. But the velocity of the falling body in C is equal to the velocity with which a circle may be uniformly described at the interval ½SC (by Prop. XXXIV). And this velocity to the velocity with which a circle may be described with the radius SK, that is, the little line Cc to the arc Kk, is (by Cor. 6, Prop. IV) in the subduplicate ratio of SK to ½SC; that is, in the ratio of SK to ½CD. Wherefore ½SK x Kk is equal to ¼CD x Cc, and therefore equal to ½SY x Dd; that is, the area KSk is equal to the area SDd, as above. Q.E.D.
Proposition xxxvi. Problem xxv.
To determine the times of the descent of a body falling from place A.
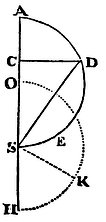
Upon the diameter AS, the distance of the body from the centre at the beginning, describe the semi-circle ADS, as likewise the semi-circle OKH equal thereto, about the centre S. From any place C of the body erect the ordinate CD. Join SD, and make the sector OSK equal to the area ASD. It is evident (by Prop. XXXV) that the body in falling will describe the space AC in the same time in which another body, uniformly revolving about the centre S, may describe the arc OK. Q.E.F.
Proposition xxxvii. Problem xxvi.
To define the times of the ascent or descent of a body projected upwards or downwards from a given place.
Suppose the body to go off from the given place G, in the direction
of the line GS, with any velocity. In the duplicate ratio of this
velocity to the uniform velocity in a circle, with which the body may
revolve about
 the centre S at the given
interval SG, take GA to ½AS. If that ratio is the same as of the
number 2 to 1, the point A is infinitely remote; in which case a
parabola is to be described with any latus rectum to the vertex S, and
axis SG; as appears by Prop. XXXIV. But if that ratio is less or
greater than the ratio of 2 to 1, in the former case a circle, in the
latter a rectangular hyperbola, is to be described on the diameter SA;
as appears by Prop. XXXIII. Then about the centre S, with an interval
equal to half the latus rectum, describe the circle HkK; and
at the place G of the ascending or descending body, and at any other
place C, erect the perpendiculars GI, CD, meeting the conic section or
circle in I and D. Then joining SI, SD, let the sectors HSK, HSk
be made equal to the segments SEIS, SEDS. and (by Prop. XXXV) the body
G will describe the space GC in the same time
in which the body K may describe the arc Kk.
Q.E.F.
the centre S at the given
interval SG, take GA to ½AS. If that ratio is the same as of the
number 2 to 1, the point A is infinitely remote; in which case a
parabola is to be described with any latus rectum to the vertex S, and
axis SG; as appears by Prop. XXXIV. But if that ratio is less or
greater than the ratio of 2 to 1, in the former case a circle, in the
latter a rectangular hyperbola, is to be described on the diameter SA;
as appears by Prop. XXXIII. Then about the centre S, with an interval
equal to half the latus rectum, describe the circle HkK; and
at the place G of the ascending or descending body, and at any other
place C, erect the perpendiculars GI, CD, meeting the conic section or
circle in I and D. Then joining SI, SD, let the sectors HSK, HSk
be made equal to the segments SEIS, SEDS. and (by Prop. XXXV) the body
G will describe the space GC in the same time
in which the body K may describe the arc Kk.
Q.E.F.
Proposition xxxviii. Theorem xii.
Supposing that the centripetal force is proportional to the altitude or distance of places from the centre. I say, that the times and velocities of falling bodies, and the spaces which they describe, are respectively proportional to the arcs, and the right and versed sines of the arcs.
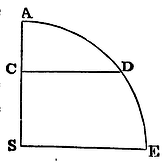
Suppose the body to fall from any place A in the right line AS; and about the centre of force S, with the interval AS, describe the quadrant of a circle AE; and let CD be the right sine of any arc AD; and the body A will in the time AD in falling describe the space AC, and in the place C will acquire the velocity CD.
This is demonstrated the same way from Prop. X, as Prop. XXXII was demonstrated from Prop. XI.
Cor. 1. Hence the times are equal in which one body falling from the place A arrives at the centre S, and another body revolving describes the quadrantal arc ADE.
Cor. 2. Wherefore all the times are equal in which bodies falling from whatsoever places arrive at the centre. For all the periodic times of revolving bodies are equal (by Cor. 3, Prop. IV).
Proposition xxxix. Problem xxvii.
Supposing a centripetal force of any kind, and granting the quadratures of curvilinear figures; it is required to find the velocity of a body, ascending or descending in a right line, in the several places through which it passes; as also the time in which it will arrive at any place: and vice versa.
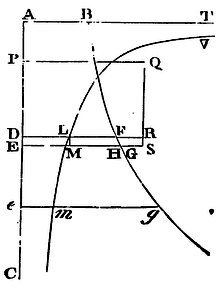
Suppose the body E to fall from any place A in the right line ADEC; and from its place E imagine a perpendicular EG always erected proportional to the centripetal force in that place tending to the centre C; and let BFG be a curve line, the locus of the point G. And in the beginning of the motion suppose EG to coincide with the perpendicular AB; and the velocity of the body in any place E will be as a right line whose square is equal to the curvilinear area ABGE. Q.E.I.
In EG take EM reciprocally proportional to a right line whose square is equal to the area ABGE, and let VLM he a curve line wherein the point M is always placed, and to which the right line AB produced is an asymptote; and the time in which the body in falling describes the line AE, will be as the curvilinear area ABTVME. Q.E.I.
For in the right line AE let there be taken the very small line DE of
a given length, and let DLF be the place of the line EMG, when the
body was in D; and if the centripetal force be such, that a right
line, whose square is equal to the area ABGE, is as the velocity of
the descending body, the area itself will be as the square of that
velocity; that is, if for the velocities in D and E we write V and V +
I, the area ABFD will be as VV, and the area ABGE as VV + 2VI + II;
and by division, the area DFGE as 2VI + II, and therefore
DFGE
DE will be as
2VI+II
DE; that is, if we take the first
ratios of those quantities when just nascent, the length DF is as the
quantity 2VI
DE, and therefore also as half that
quantity I x V
DE. But the time in which the body in
falling describes the verv small line DE, is as that line directly and
the velocity V inversely; and the force will be as the increment I of
the velocity directly and the time inversely; and therefore if we take
the first ratios when those quantities are just nascent, as
I x V
DE, that is, as the length DF.
Therefore a force proportional to DF or EG will cause the body to
descend with a velocity that is as the right line whose square is
equal to the area ABGE. Q.E.D.
Moreover, since the time in which a very small line DE of a given length may be described is as the velocity inversely, and therefore also inversely as a right line whose square is equal to the area ABFD; and since the line DL, and by consequence the nascent area DLME, will be as the same right line inversely, the time will be as the area DLME, and the sum of all the times will be as the sum of all the areas; that is (by Cor. Lem. IV), the whole time in which the line AE is described will be as the whole area ATVME. Q.E.D.
Cor. 1. Let P be the place from whence a body
ought to fall, so as that, when urged by any known uniform centripetal
force (such as gravity is vulgarly supposed to be), it may acquire in
the place D a velocity equal to the velocity which another body,
falling by any force whatever, hath acquired in that place D. In the
perpendicular DF let there be taken DR, which may be to DF as that
uniform force to the other force in the place D. Complete the
rectangle PDRQ, and cut off the area ABFD equal to that rectangle.
Then A will be the place
 from whence the other body fell. For completing the rectangle DRSE,
since the area ABFD is to the area DFGE as VV to 2VI, and therefore as
½V to I, that is, as half the whole velocity to the increment of the
velocity of the body falling by the unequable force; and in like
manner the area PQRD to the area DRSE as half the whole velocity to
the increment of the velocity of the body falling by the uniform
force; and since those increments (by reason of the equality of the
nascent times) are as the generating forces, that is, as the ordinates
DF, DR, and consequently as the nascent areas DFGE, DRSE: therefore, ex
aequo, the whole areas ABFD, PQRD will be to one another as the
halves of the whole velocities; and therefore, because the velocities
are equal, they become equal also.
from whence the other body fell. For completing the rectangle DRSE,
since the area ABFD is to the area DFGE as VV to 2VI, and therefore as
½V to I, that is, as half the whole velocity to the increment of the
velocity of the body falling by the unequable force; and in like
manner the area PQRD to the area DRSE as half the whole velocity to
the increment of the velocity of the body falling by the uniform
force; and since those increments (by reason of the equality of the
nascent times) are as the generating forces, that is, as the ordinates
DF, DR, and consequently as the nascent areas DFGE, DRSE: therefore, ex
aequo, the whole areas ABFD, PQRD will be to one another as the
halves of the whole velocities; and therefore, because the velocities
are equal, they become equal also.
Cor. 2. Whence if any body be projected either upwards or downwards with a given velocity from any place D, and there be given the law of centripetal force acting on it, its velocity will be found in any other place, as e, by erecting the ordinate eg, and taking that velocity to the velocity in the place D as a right line whose square is equal to the rectangle PQRD, either increased by the curvilinear area DFge, if the place e is below the place D, or diminished by the same area DFge, if it be higher, is to the right line whose square is equal to the rectangle PQRD alone.
Cor. 3. The time is also known by erecting the ordinate em reciprocally proportional to the square root of PQRD + or − DFge, and taking the time in which the body has described the line De to the time in which another body has fallen with an uniform force from P, and in falling arrived at D in the proportion of the curvilinear area DLme to the rectangle 2PD x DL. For the time in which a body falling with an uniform force hath described the line PD, is to the time in which the same body has described the line PE in the subduplicate ratio of PD to PE; that is (the very small line DE being just nascent), in the ratio of PD to PD + ½DE, or 2PD to 2PD + DE, and, by division, to the time in which the body hath described the small line DE, as 2PD to DE, and therefore as the rectangle 2PD x DL to the area DLME; and the time in which both the bodies described the very small line DE is to the time in which the body moving unequably hath described the line De as the area DLME to the area DLme; and, ex aequo, the first mentioned of these times is to the last as the rectangle 2PD x DL to the area DLme.