Section iii.
Of the motion of bodies in eccentric conic sections.
Proposition xi. Problem vi.
If a body revolves in an ellipsis; it is required to find the law of the centripetal force tending to the focus of the ellipsis.
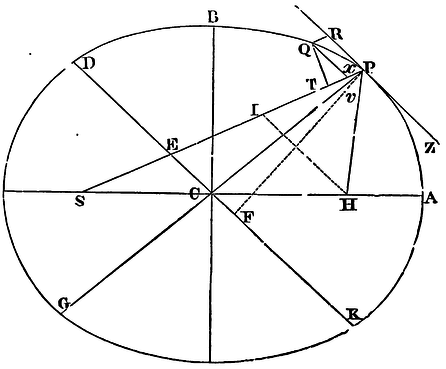
Let S be the focus of the ellipsis. Draw SP cutting the diameter DK
of the ellipsis in E, and the ordinate Qv in x; and
complete the parallelogram QxPR. It is evident that EP is
equal to the greater semi-axis AC: for drawing HI from the other focus
H of the ellipsis parallel to EC, because CS, CH are equal, ES, EI
will be also equal; so that EP is the half sum of PS, PI, that is
(because of the parallels HI, PR, and the equal angles IPR, HPZ), of
PS, PH, which taken together are equal to the whole axis 2AC. Draw QT
perpendicular to SP, and putting L for the principal latus rectum of
the ellipsis (or for
2BC2
AC ), we shall have L x QR to L x Pv
as QR to Pv, that is, as PE or AC to PC; and L x Pv
to GvP as L to Gv; and GvP to Qv²
as PC² to CD²; and by (Corol. 2, Lem. VII) the points Q and P
coinciding, Qv² is to Qx² in the ratio of equality;
and Qx² or Qv² is to QT² as EP² to PF², that is, as
CA² to PF², or (by Lem. XII) as CD² to CB². And compounding all those
ratios together, we shall have L x QR to
QT² as AC x L x PC² x CD², or 2CB²
x PC² x CD² to PC x Gv x CD² x CB²,
or as 2PC to Gv. But the points Q and P coinciding, 2PC and Gv
are equal. And therefore the quantities L x QR
and QT², proportional to these, will be also equal. Let those equals
be drawn into SP2
QR, and L x SP² will become equal to
SP2 x QT2
QR. And therefore (by Corol. 1 and 5, Prop. VI) the
centripetal force is reciprocally as L x SP², that is, reciprocally in
the duplicate ratio of the distance SP. Q.E.I.
The same otherwise.
Since the force tending to the centre of the ellipsis, by which the
body P may revolve in that ellipsis, is (by Corol. 1, Prop. X.) as the
distance CP of the body from the centre C of the ellipsis; let CE be
drawn parallel to the tangent PR of the ellipsis; and the force by
which the same body P may revolve about any other point's of the
ellipsis, if CE and PS intersect in E, will be as
PE3
SP2 (by Cor. 3, Prop. VII.);
that is, if the point S is the focus of the ellipsis, and therefore PE
be given as SP² reciprocally. Q.E.I.
With the same brevity with which we reduced the fifth Problem to the parabola, and hyperbola, we might do the like here: but because of the dignity of the Problem and its use in what follows. I shall confirm the other cases by particular demonstrations.
Proposition xii. Problem vii.
Suppose a body to move in an hyperbola; it is required to find the law of the centripetal force tending to the focus of that figure.
Let CA, CB be the semi-axes of the hyperbola; PG, KD other conjugate
diameters; PF a perpendicular to the diameter KD; and Qv an
ordinate to the diameter GP. Draw SP cutting the diameter DK in E, and
the ordinate Qv in x, and complete the
parallelogram QRPx. It is evident that EP is equal to the
semi-transverse axis AC; for drawing HI, from the other focus H of the
hyperbola, parallel to EC, because CS, CH are equal, ES, EI will be
also equal; so that EP is the half difference
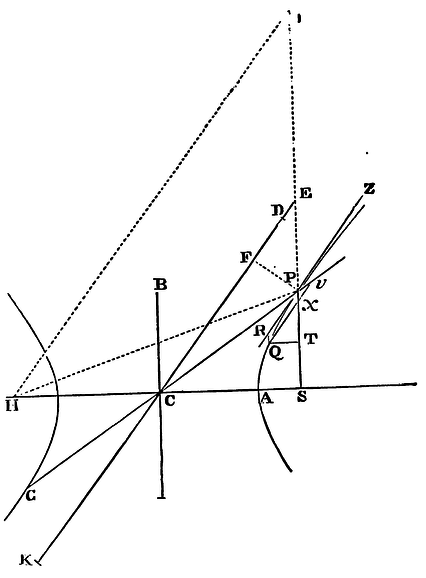 of PS, PI; that is (because of the parallels
IH, PR, and the equal angles IPR, HPZ), of PS, PH, the difference of
which is equal to the whole axis 2AC. Draw QT perpendicular to SP; and
putting L for the principal latus rectum of the hyperbola (that is,
for 2BC2
of PS, PI; that is (because of the parallels
IH, PR, and the equal angles IPR, HPZ), of PS, PH, the difference of
which is equal to the whole axis 2AC. Draw QT perpendicular to SP; and
putting L for the principal latus rectum of the hyperbola (that is,
for 2BC2
AC, we shall have L x QR to L x Pv
as QR to Pv, or Px to Pv, that is (because
of the similar triangles Pxv, PEC), as PE to PC, or AC to PC.
And L x Pv will be to Gv x Pv as L to Gv;
and (by the properties of the conic sections) the rectangle GvP
is to Qv² as PC² to CD²; and by (Cor. 2, Lem. VII.), Qv²
to Qx² the points Q and P coinciding, becomes a ratio of
equality; and Qx² or Qv² is to QT² as EP² to PF²,
that is, as CA² to PF², or (by Lem. XII.) as CD² to CB²: and,
compounding all those ratios together, we shall have L x QR to QT² as
AC x L x PC² x CD², or 2CB² x PC² x CD² to PC x Gv x CD² x
CB², or as 2PC to Gv. But the points P and Q coinciding, 2PC
and Gv are equal. And therefore the quantities L x QR and
QT², proportional to them, will be also equal. Let those equals be
drawn into SP2
QR, and we shall have L x SP² equal to
SP2 x QT2
QR. And therefore (by Cor. I and 5, Prop. VI.) the
centripetal force is reciprocally as L x SP², that is, reciprocally in
the duplicate ratio of the distance SP. Q.E.I.
Find out the force tending from the centre C of the hyperbola. This
will be proportional to the distance CP. But from thence (by Cor. 3,
Prop. VII.) the force tending to the focus S will be as
PE3
SP2, that is, because PE is
given reciprocally as SP². Q.E.I.
And the same way may it be demonstrated, that the body having its centripetal changed into a centrifugal force, will move in the conjugate hyperbola.
Lemma xiii.
The latus rectum of a parabola belonging to any vertex is quadruple the distance of that vertex from the focus of the figure.
This is demonstrated by the writers on the conic sections.
Lemma xiv.
The perpendicular, let fall from the focus of a parabola on its tangent, is a mean proportional between the distances of the focus from the point of contact, and from the principal vertex of the figure.
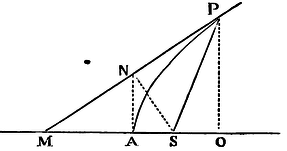
For, let AP be the parabola, S its focus, A its principal vertex, P the point of contact, PO an ordinate to the principal diameter, PM the tangent meeting the principal diameter in M, and SN the perpendicular from the focus on the tangent: join AN, and because of the equal lines MS and SP, MN and NP, MA and AO, the right lines AN, OP, will be parallel; and thence the triangle SAN will be right-angled at A, and similar to the equal triangles SNM, SNP; therefore PS is to SN as SN to SA. Q.E.D.
Cor. 1. PS² is to SN² as PS to SA.
Cor. 2. And because SA is given, SN² will be as PS.
Cor. 3. And the concourse of any tangent PM, with the right line SN. drawn from the focus perpendicular on the tangent, falls in the right line AN that touches the parabola in the principal vertex.
Proposition xiii. Problem viii.
If a body moves in the perimeter of a parabola; it is required to find the law of the centripetal force tending to the focus of that figure.
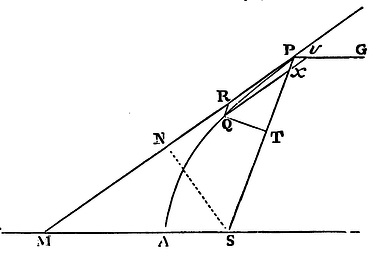
Retaining the construction of the preceding Lemma, let P be the body
in the perimeter of the parabola; and from the place Q, into which it
is next to succeed, draw QR parallel and QT perpendicular to SP, as
also Qv parallel to the tangent, and meeting the diameter PG
in v, and the distance SP in x.
Now, because of the similar triangles Pxv, SPM, and of the
equal sides SP, SM of the one, the sides Px or QR and Pv
of the other will be also equal. But (by the conic sections) the
square of the ordinate Qv is equal to the rectangle under the
latus rectum and the segment Pv of the diameter; that is (by
Lem. XIII.), to the rectangle 4PS x Pv, or 4PS x QR; and the
points P and Q coinciding, the ratio of Qv to Qx (by
Cor. 2, Lem. VII.,) becomes a ratio of equality. And therefore Qx²,
in this case, becomes equal to the rectangle 4PS x QR. But (because of
the similar triangles QxT, SPN), Qx² is to QT² as
PS² to SN², that is (by Cor. 1, Lem. XIV.), as PS to SA; that is, as
4PS x QR to 4SA x QR, and therefore (by Prop. IX. Lib. V., Elem.) QT²
and 4SA x QR are equal. Multiply these equals by
SP2
QR, and SP2 x
QT2
QR will become equal to SP² x 4SA: and therefore (by Cor. 1
and 5, Prop. VI.), the centripetal force is reciprocally as SP² x 4SA;
that is, because 4SA is given; reciprocally in the duplicate ratio of
the distance SP. Q.E.I.
Cor. 1. From the three last Propositions it follows, that if any body P goes from the place P with any velocity in the direction of any right line PR, and at the same time is urged by the action of a centripetal force that is reciprocally proportional to the square of the distance of the places from the centre, the body will move in one of the conic sections, having its focus in the centre of force; and the contrary. For the focus, the point of contact, and the position of the tangent, being given, a conic section may be described, which at that point shall have a given curvature. But the curvature is given from the centripetal force and velocity of the body being given; and two orbits, mutually touching one the other, cannot be described by the same centripetal force and the same velocity.
Cor. 2. If the velocity with which the body
goes from its place P is such, that in any infinitely small moment of
time the lineola PR may be thereby described; and the centripetal
force such as in the same time to move the same body through the space
QR; the body will move in one of the conic sections, whose principal
latus rectum is the quantity QT2
QR in its ultimate state, when the
lineolae PR, QR are diminished in infinitum. In these
Corollaries I consider the circle as an ellipsis; and I except the
case where the body descends to the centre in a right line.
Proposition xiv. Theorem vi.
If several bodies revolve about one common centre, and the centripetal force is reciprocally in the duplicate ratio of the distance of places from the centre; I say, that the principal latera recta of their orbits are in the duplicate ratio of the areas, which the bodies by radii drawn to the centre describe in the same time.
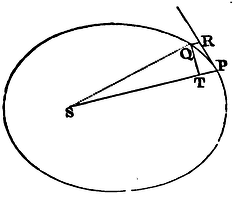
For (by Cor. 2, Prop. XIII) the latus rectum L is equal to the
quantity QT2
QR in its ultimate state when the
points P and Q coincide. But the lineola QR in a given time is as the
generating centripetal force; that is (by supposition), reciprocally
as SP² . And therefore QT2
QR is as QT² x SP²; that is, the latus
rectum L is in the duplicate ratio of the area QT x SP.
Q.E.D.
Cor. Hence the whole area of the ellipsis, and the rectangle under the axes, which is proportional to it, is in the ratio compounded of the subduplicate ratio of the latus rectum, and the ratio of the periodic time. For the whole area is as the area QT x SP, described in a given time, multiplied by the periodic time.
Proposition xv. Theorem vii.
The same things being supposed, I say, that the periodic times in ellipses are in the sesquiplicate ratio of their greater axes.
For the lesser axis is a mean proportional between the greater axis and the latus rectum; and, therefore, the rectangle under the axes is in the ratio compounded of the subduplicate ratio of the latus rectum and the sesquiplicate ratio of the greater axis. But this rectangle (by Cor. 3. Prop. XIV) is in a ratio compounded of the subduplicate ratio of the latus rectum, and the ratio of the periodic time. Subduct from both sides the subduplicate ratio of the latus rectum, and there will remain the sesquiplicate ratio of the greater axis, equal to the ratio of the periodic time. Q.E.D.
Cor. Therefore the periodic times in ellipses are the same as in circles whose diameters are equal to the greater axes of the ellipses.
Proposition xvi. Theorem viii.
The same things being supposed, and right lines being drawn to the bodies that shall touch the orbits, and perpendiculars being let fall on those tangents from the common focus; I say, that the velocities of the bodies are in a ratio compounded of the ratio of the perpendiculars inversely, and the subduplicate ratio of the principal latera recta directly.
From the focus S draw SY perpendicular to the tangent PR, and the
velocity of the body P will be reciprocally in the subduplicate ratio
of the quantity SY2
L. For that velocity is as the
infinitely small arc PQ described
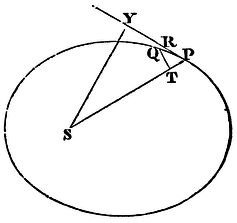 in a given moment of time, that is (by Lem. VII), as the tangent PR;
that is (because of the proportionals PR to QT, and SP to SY), as
SP x QT
in a given moment of time, that is (by Lem. VII), as the tangent PR;
that is (because of the proportionals PR to QT, and SP to SY), as
SP x QT
SY; or as SY reciprocally, and SP x QT
directly; but SP x QT is as the area described in the given time, that
is (by Prop. XIV), in the subduplicate ratio of the latus rectum.
Q.E.D.
Cor. 1. The principal latera recta are in a ratio compounded of the duplicate ratio of the perpendiculars and the duplicate ratio of the velocities.
Cor. 2. The velocities of bodies, in their greatest and least distances from the common focus, are in the ratio compounded of the ratio of the distances inversely, and the subduplicate ratio of the principal latera recta directly. For those perpendiculars are now the distances.
Cor. 3. And therefore the velocity in a conic section, at its greatest or least distance from the focus, is to the velocity in a circle, at the same distance from the centre, in the subduplicate ratio of the principal latus rectum to the double of that distance.
Cor. 4. The velocities of the bodies revolving in ellipses, at their mean distances from the common focus, are the same as those of bodies revolving in circles, at the same distances; that is (by Cor. 6, Prop. IV), reciprocally in the subduplicate ratio of the distances. For the perpendiculars are now the lesser semi-axes, and these are as mean proportionals between the distances and the latera recta. Let this ratio inversely be compounded with the subduplicate ratio of the latera recta directly, and we shall have the subduplicate ratio of the distance inversely.
Cor. 5. In the same figure, or even in different figures, whose principal latera recta are equal, the velocity of a body is reciprocally as the perpendicular let fall from the focus on the tangent.
Cor. 6. In a parabola, the velocity is reciprocally in the subduplicate ratio of the distance of the body from the focus of the figure; it is more variable in the ellipsis, and less in the hyperbola, than according to this ratio. For (by Cor. 2, Lem. XIV) the perpendicular let fall from the focus on the tangent of a parabola is in the subduplicate ratio of the distance. In the hyperbola the perpendicular is less variable; in the ellipsis more.
Cor. 7. In a parabola, the velocity of a body at any distance from the focus is to the velocity of a body revolving in a circle, at the same distance from the centre, in the subduplicate ratio of the number 2 to 1; in the ellipsis it is less, and in the hyperbola greater, than according to this ratio, (by Cor. 2 of this Prop.) the velocity at the vertex of a parabola is in this ratio, and (by Cor. 6 of this Prop. and Prop. IV) the same proportion holds in all distances. And hence, also, in a parabola, the velocity is everywhere equal to the velocity of a body revolving in a circle at half the distance; in the ellipsis it is less, and in the hyperbola greater.
Cor. 8. The velocity of a body revolving in any conic section is to the velocity of a body revolving in a circle, at the distance of half the principal latus rectum of the section, as that distance to the perpendicular let fall from the focus on the tangent of the section. This appears from Cor. 5.
Cor. 9. Wherefore since (by Cor. 6, Prop. IV), the velocity of a body revolving in this circle is to the velocity of another body revolving in any other circle reciprocally in the subduplicate ratio of the distances; therefore, ex aequo, the velocity of a body revolving in a conic section will be to the velocity of a body revolving in a circle at the same distance as a mean proportional between that common distance, and half the principal latus rectum of the section, to the perpendicular let fall from the common focus upon the tangent of the section.
Proposition xvii. Problem ix.
Supposing the centripetal force to be reciprocally proportional to the squares of the distances of places from the centre, and that the absolute quantity of that force is known; it is required to determine the line which a body will describe that is let go from a given place with a given velocity in, the direction of a given right line.
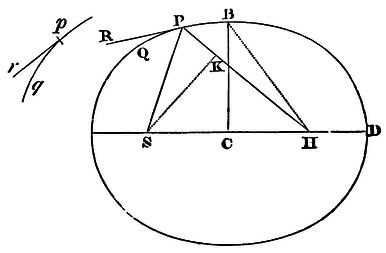
Let the centripetal force tending to the point S be such as will make the body p revolve in any given orbit pq; and suppose the velocity of this body in the place p is known. Then from the place P suppose the body P to be let with a given velocity in the direction of the line PR; but by virtue of a centripetal force to be immediately turned aside from that right line into the conic section PQ. This, the right line PR will therefore touch in P. Suppose likewise that the right line pr touches the orbit pq in p, and if from S you suppose perpendiculars let fall on those tangents, the principal latus rectum of the conic section (by Cor. 1, Prop. XVI) will be to the principal latus rectum of that orbit in a ratio compounded of the duplicate ratio of the perpendiculars, and the duplicate ratio of the velocities; and is therefore given. Let this latus rectum be L; the focus S of the conic section is also given. Let the angle RPH be the complement of the angle RPS to two right; and the line PH, in which the other focus H is placed, is given by position. Let fall SK perpendicular on PH, and erect the conjugate semi-axis BC; this done, we shall have SP2 − 2KPH + PH2 = SH2 = 4CH2 = 4BH2 − 4BC2 = (SP + PH2) − L x (SP + PH) = SP2 + 2SPH + PH2 − L x (SP + PH). Add on both sides 2KPH − SP2 − PH2 + L x (SP + PH), and we shall have L x (SP + PH) = 2SPH + 2KPH, or SP + PH to PH, as 2SP + 2KP to L. Whence PH is given both in length and position. That is, if the velocity of the body in P is such that the latus rectum L is less than 2SP + 2KP, PH will lie on the same side of the tangent PR with the line SP; and therefore the figure will be an ellipsis, which from the given foci S, H, and the principal axis SP + PH, is given also. But if the velocity of the body is so great, that the latus rectum L becomes equal to 2SP + 2KP, the length PH will be infinite; and therefore, the figure will be a parabola, which has its axis SH parallel to the line PK, and is thence given. But if the body goes from its place P with a yet greater velocity, the length PH is to be taken on the other side the tangent; and so the tangent passing between the foci, the figure will be an hyperbola having its principal axis equal to the difference of the lines SP and PH, and thence is given. For if the body, in these cases, revolves in a conic section so found, it is demonstrated in Prop. XI, XII, and XIII, that the centripetal force will be reciprocally as the square of the distance of the body from the centre of force S; and therefore we have rightly determined the line PQ, which a body let go from a given place P with a given velocity, and in the direction of the right line PR given by position, would describe with such a force. Q.E.F.
Cor. 1. Hence in every conic section, from the principal vertex D, the latus rectum L, and the focus S given, the other focus H is given, by taking DH to DS as the latus rectum to the difference between the latus rectum and 4DS. For the proportion, SP + PH to PH as 2SP + 2KP to L, becomes, in the case of this Corollary, DS + DH to DH as 4DS to L, and by division DS to DH as 4DS − L to L.
Cor. 2. Whence if the velocity of a body in the principal vertex D is given, the orbit may be readily found; to wit, by taking its latus rectum to twice the distance DS, in the duplicate ratio of this given velocity to the velocity of a body revolving in a circle at the distance DS (by Cor. 3, Prop. XVI.), and then taking DH to DS as the latus rectum to the difference between the latus rectum and 4DS.
Cor. 3. Hence also if a body move in any conic section, and is forced out of its orbit by any impulse, you may discover the orbit in which it will afterwards pursue its course. For by compounding the proper motion of the body with that motion, which the impulse alone would generate, you will have the motion with which the body will go off from a given place of impulse in the direction of a right line given in position.
Cor. 4. And if that body is continually disturbed by the action of some foreign force, we may nearly know its course, by collecting the changes which that force introduces in some points, and estimating the continual changes it will undergo in the intermediate places, from the analogy that appears in the progress of the series.
Scholium.
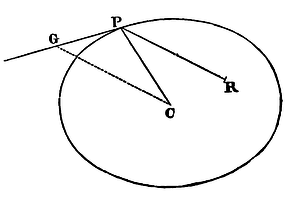
If a body P, by means of a centripetal force tending to any given
point R, move in the perimeter of any given conic section whose centre
is C; and the law of the centripetal force is required: draw CG
parallel to the radius RP, and meeting the tangent PG of the orbit in
G; and the force required (by Cor. 1, and Schol. Prop. X., and Cor. 3,
Prop. VII.) will be as CG3
RP2.