Section ii.
Of the Invention of Centripetal Forces.
Proposition i. Theorem I.
The areas, which revolving bodies describe by radii drawn to an immovable centre of force do lie in the same immovable planes, and are proportional to the times in which they are described.
For suppose the time to be divided into equal parts, and in the first
part of that time let the body by its innate force describe the right
line AB In the second part of that time, the same would (by Law I.),
if not hindered, proceed directly to c, along the line Bc
equal to AB; so that by the radii AS, BS, cS, drawn to the
centre, the equal areas ASB, BSc, would be described.
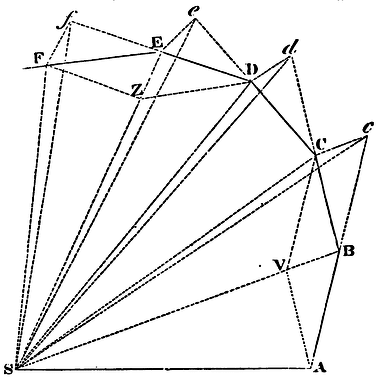 But when the body is arrived at
B, suppose that a centripetal force acts at once with a great impulse;
and, turning aside the body from the right line Bc, compels
it afterwards to continue its motion along the right line BC. Draw cC
parallel to BS meeting BC in C; and at the end of the second part of
the time, the body (by Cor. I. of the Laws) will be found in C, in the
same plane with the triangle ASB. Join SC, and, because SB and Cc
are parallel, the triangle SBC will be equal to the triangle SBc,
and therefore also to the triangle SAB. By the like argument, if the
centripetal force acts successively in C, D, E. &c.; and makes the
body, in each single particle of time, to describe the right lines CD,
DE, EF, &c., they will all lie in the same plane; and the triangle
SCD will be equal to the triangle SBC, and SDE to SCD, and SEF to SDE.
And therefore, in equal times, equal areas are described in one
immovable plane: and, by composition, any sums SADS, SAFS, of those
areas, are one to the other as the times in which they are described.
Now let the number of those triangles be augmented, and their breadth
diminished in infinitum; and (by Cor. 4, Lem. III.) their
ultimate perimeter ADF will be a curve line: and therefore the
centripetal force, by which the body is perpetually drawn back from
the tangent of this curve, will act continually; and any described
areas SADS, SAFS, which are always proportional to the times of
description, will, in this case also, be proportional to those times.
Q.E.D.
But when the body is arrived at
B, suppose that a centripetal force acts at once with a great impulse;
and, turning aside the body from the right line Bc, compels
it afterwards to continue its motion along the right line BC. Draw cC
parallel to BS meeting BC in C; and at the end of the second part of
the time, the body (by Cor. I. of the Laws) will be found in C, in the
same plane with the triangle ASB. Join SC, and, because SB and Cc
are parallel, the triangle SBC will be equal to the triangle SBc,
and therefore also to the triangle SAB. By the like argument, if the
centripetal force acts successively in C, D, E. &c.; and makes the
body, in each single particle of time, to describe the right lines CD,
DE, EF, &c., they will all lie in the same plane; and the triangle
SCD will be equal to the triangle SBC, and SDE to SCD, and SEF to SDE.
And therefore, in equal times, equal areas are described in one
immovable plane: and, by composition, any sums SADS, SAFS, of those
areas, are one to the other as the times in which they are described.
Now let the number of those triangles be augmented, and their breadth
diminished in infinitum; and (by Cor. 4, Lem. III.) their
ultimate perimeter ADF will be a curve line: and therefore the
centripetal force, by which the body is perpetually drawn back from
the tangent of this curve, will act continually; and any described
areas SADS, SAFS, which are always proportional to the times of
description, will, in this case also, be proportional to those times.
Q.E.D.
Cor. 1. The velocity of a body attracted towards an immovable centre, in spaces void of resistance, is reciprocally as the perpendicular let fall from that centre on the right line that touches the orbit. For the velocities in those places A, B, C, D, E, are as the bases AB, BC, CD, DE, EF, of equal triangles; and these bases are reciprocally as the perpendiculars let fall upon them.
Cor. 2. If the chords AB, BC of two arcs, successively described in equal times by the same body, in spaces void of resistance, are completed into a parallelogram ABCV, and the diagonal BV of this parallelogram; in the position which it ultimately acquires when those arcs are diminished in infinitum, is produced both ways, it will pass through the centre of force.
Cor. 3. If the chords AB, BC, and DE, EF, of arcs described in equal times, in spaces void of resistance, are completed into the parallelograms ABCV, DEFZ; the forces in B and E are one to the other in the ultimate ratio of the diagonals BV, EZ, when those arcs are diminished in infinitum. For the motions BC and EF of the body (by Cor. 1 of the Laws) are compounded of the motions Bc, BV, and Ef, EZ: but BV and EZ, which are equal to Cc and Ff, in the demonstration of this Proposition, were generated by the impulses of the centripetal force in B and E, and are therefore proportional to those impulses.
Cor. 4. The forces by which bodies, in spaces void of resistance, are drawn back from rectilinear motions, and turned into curvilinear orbits, are one to another as the versed sines of arcs described in equal times; which versed sines tend to the centre of force, and bisect the chords when those arcs are diminished to infinity. For such versed sines are the halves of the diagonals mentioned in Cor. 3.
Cor. 5. And therefore those forces are to the force of gravity as the said versed sines to the versed sines perpendicular to the horizon of those parabolic arcs which projectiles describe in the same time.
Cor. 6. And the same things do all hold good (by Cor. 5 of the Laws), when the planes in which the bodies are moved, together with the centres of force which are placed in those planes, are not at rest, but move uniformly forward in right lines.
Proposition ii. Theorem ii.
Every body that moves in any curve line described in a plane, and by a radius, drawn to a point either immovable, or moving forward with an uniform rectilinear motion, describes about that point areas proportional to the times, is urged by a centripetal force directed to that point.

Case. 1. For every body that moves in a curve line, is (by Law 1) turned aside from its rectilinear course by the action of some force that impels it. And that force by which the body is turned off from its rectilinear course, and is made to describe, in equal times, the equal least triangles SAB, SBC, SCD, &c., about the immovable point S (by Prop. XL. Book 1, Elem. and Law II), acts in the place B, according to the direction of a line parallel to cC, that is, in the direction of the line BS, and in the place C, according to the direction of a line parallel to dD, that is, in the direction of the line CS, &c.; and therefore acts always in the direction of lines tending to the immovable point S. Q.E.D.
Case. 2. And (by Cor. 5 of the Laws) it is indifferent whether the superfices in which a body describes a curvilinear figure be quiescent, or moves together with the body, the figure described, and its point S, uniformly forward in right lines.
Cor. 1. In non-resisting spaces or mediums, if the areas are not proportional to the times, the forces are not directed to the point in which the radii meet; but deviate therefrom in consequentia, or towards the parts to which the motion is directed, if the description of the areas is accelerated; but in antecedentia, if retarded.
Cor. 2. And even in resisting mediums, if the description of the areas is accelerated, the directions of the forces deviate from the point in which the radii meet; towards the parts to which the motion tends.
Scholium.
A body may be urged by a centripetal force compounded of several forces; in which case the meaning of the Proposition is, that the force which results out of all tends to the point S. But if any force acts perpetually in the direction of lines perpendicular to the described surface, this force will make the body to deviate from the plane of its motion: but will neither augment nor diminish the quantity of the described surface, and is therefore to be neglected in the composition of forces.
Proposition iii. Theorem iii.
Every body, that by a radius drawn to the centre of another body, how soever moved, describes areas about that centre proportional to the times, is urged by a force compounded out of the centripetal force tending to that other body, and of all the accelerative force by which that other body is impelled.
Let L represent the one, and T the other body; and (by Cor. 6 of the Laws) if both bodies are urged in the direction of parallel lines, by a new force equal and contrary to that by which the second body T is urged, the first body L will go on to describe about the other body T the same areas as before: but the force by which that other body T was urged will be now destroyed by an equal and contrary force; and therefore (by Law I.) that other body T, now left to itself, will either rest, or move uniformly forward in a right line: and the first body L impelled by the difference of the forces, that is, by the force remaining, will go on to describe about the other body T areas proportional to the times. And therefore (by Theor. II.) the difference of the forces is directed to the other body T as its centre. Q.E.D
Cor. 1. Hence if the one body L, by a radius drawn to the other body T, describes areas proportional to the times; and from the whole force, by which the first body L is urged (whether that force is simple, or, according to Cor. 2 of the Laws, compounded out of several forces), we subduct (by the same Cor.) that whole accelerative force by which the other body is urged; the whole remaining force by which the first body is urged will tend to the other body T, as its centre.
Cor. 2. And, if these areas are proportional to the times nearly, the remaining force will tend to the other body T nearly.
Cor. 3. And vice versa, if the remaining force tends nearly to the other body T, those areas will be nearly proportional to the times.
Cor. 4. If the body L, by a radius drawn to the other body T, describes areas, which, compared with the times, are very unequal; and that other body T be either at rest, or moves uniformly forward in a right line: the action of the centripetal force tending to that other body T is either none at all, or it is mixed and compounded with very powerful actions of other forces: and the whole force compounded of them all, if they are many, is directed to another (immovable or moveable) centre. The same thing obtains, when the other body is moved by any motion whatsoever; provided that centripetal force is taken, which remains after subducting that whole force acting upon that other body T.
Scholium.
Because the equable description of areas indicates that a centre is respected by that force with which the body is most affected, and by which it is drawn back from its rectilinear motion, and retained in its orbit; why may we not be allowed, in the following discourse, to use the equable description of areas as an indication of a centre, about which all circular motion is performed in free spaces?
Proposition iv. Theorem iv.
The centripetal forces of bodies, which by equable motions describe different circles, tend to the centres of the same circles; and are one to the other as the squares of the arcs described in equal times applied to the radii of the circles.
These forces tend to the centres of the circles (by Prop. II., and Cor. 2, Prop. I.), and are one to another as the versed sines of the least arcs described in equal times (by Cor. 4, Prop. I.); that is, as the squares of the same arcs applied to the diameters of the circles (by Lem. VII.); and therefore since those arcs are as arcs described in any equal times, and the diameters are as the radii, the forces will be as the squares of any arcs described in the same time applied to the radii of the circles. Q.E.D.
Cor. 1. Therefore, since those arcs are as the velocities of the bodies the centripetal forces are in a ratio compounded of the duplicate ratio of the velocities directly, and of the simple ratio of the radii inversely.
Cor. 2. And since the periodic times are in a ratio compounded of the ratio of the radii directly, and the ratio of the velocities inversely, the centripetal forces, are in a ratio compounded of the ratio of the radii directly, and the duplicate ratio of the periodic times inversely.
Cor. 3. Whence if the periodic times are equal, and the velocities therefore as the radii, the centripetal forces will be also as the radii; and the contrary.
Cor. 4. If the periodic times and the velocities are both in the subduplicate ratio of the radii, the centripetal forces will be equal among themselves; and the contrary.
Cor. 5. If the periodic times are as the radii, and therefore the velocities equal, the centripetal forces will be reciprocally as the radii; and the contrary.
Cor. 6. If the periodic times are in the sesquiplicate ratio of the radii, and therefore the velocities reciprocally in the subduplicate ratio of the radii, the centripetal forces will be in the duplicate ratio of the radii inversely; and the contrary.
Cor. 7. And universally, if the periodic time is as any power Rn of the radius R, and therefore the velocity reciprocally as the power Rn−1 of the radius, the centripetal force will be reciprocally as the power R2n−1 of the radius; and the contrary.
Cor. 8. The same things all hold concerning the times, the velocities, and forces by which bodies describe the similar parts of any similar figures that have their centres in a similar position with those figures; as appears by applying the demonstration of the preceding cases to those. And the application is easy, by only substituting the equable description of areas in the place of equable motion, and using the distances of the bodies from the centres instead of the radii.
Cor. 9. From the same demonstration it likewise follows, that the arc which a body, uniformly revolving in a circle by means of a given centripetal force, describes in any time, is a mean proportional between the diameter of the circle, and the space which the same body falling by the same given force would descend through in the same given time.
Scholium.
The case of the 6th Corollary obtains in the celestial bodies (as Sir Christopher Wren, Dr. Hooke, and Dr. Halley have severally observed); and therefore in what follows, I intend to treat more at large of those things which relate to centripetal force decreasing in a duplicate ratio of the distances from the centres.
Moreover, by means of the preceding Proposition and its Corollaries, we may discover the proportion of a centripetal force to any other known force, such as that of gravity. For if a body by means of its gravity revolves in a circle concentric to the earth, this gravity is the centripetal force of that body. But from the descent of heavy bodies, the time of one entire revolution, as well as the arc described in any given time, is given (by Cor. 9 of this Prop.). And by such propositions, Mr. Huygens, in his excellent book De Horologio Oscillatorio, has compared the force of gravity with the centrifugal forces of revolving bodies.
The preceding Proposition may be likewise demonstrated after this manner. In any circle suppose a polygon to be inscribed of any number of sides. And if a body, moved with a given velocity along the sides of the polygon, is reflected from the circle at the several angular points, the force, with which at every reflection it strikes the circle, will be as its velocity: and therefore the sum of the forces, in a given time, will be as that velocity and the number of reflections conjunctly: that is (if the species of the polygon be given), as the length described in that given time, and increased or diminished in the ratio of the same length to the radius of the circle; that is, as the square of that length applied to the radius; and therefore the polygon, by having its sides diminished in infinitum, coincides with the circle, as the square of the arc described in a given time applied to the radius. This is the centrifugal force, with which the body impels the circle; and to which the contrary force, wherewith the circle continually repels the body towards the centre, is equal.
Proposition v. Problem I.
There being given, in any places, the velocity with which a body describes a given figure, by means of forces directed to some common centre: to find that centre.
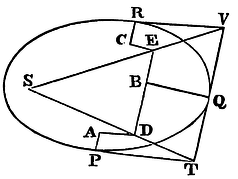
Let the three right lines PT, TQV, VR touch the figure described in as many points, P, Q, R, and meet in T and V. On the tangents erect the perpendiculars PA, QB, RC, reciprocally proportional to the velocities of the body in the points P, Q, R, from which the perpendiculars were raised; that is, so that PA may be to QB as the velocity in Q, to the velocity in P, and QB to RC as the velocity in R to the velocity in Q. Through the ends A, B, C, of the perpendiculars draw AD, DBE, EC, at right angles, meeting in D and E: and the right lines TD, VE produced, will meet in S, the centre required.
For the perpendiculars let fall from the centre S on the tangents PT, QT, are reciprocally as the velocities of the bodies in the points P and Q (by Cor. 1, Prop. I.), and therefore, by construction, as the perpendiculars AP, BQ directly; that is, as the perpendiculars let fall from the point D on the tangents. Whence it is easy to infer that the points S, D, T, are in one right line. And by the like argument the points S, E, V are also in one right line; and therefore the centre S is in the point where the right lines TD, VE meet. Q.E.D.
Proposition vi. Theorem V.
In a space void of resistance, if a body revolves in any orbit about an immovable centre, and in the least time describes any arc just then nascent; and the versed sine of that arc is supposed to be drawn bisecting the chord, and produced passing through the centre of force: the centripetal force in the middle of the arc will be as the versed sine directly and the square of the time inversely.
For the versed sine in a given time is as the force (by Cor. 4, Prop. 1); and augmenting the time in any ratio, because the arc will be augmented in the same ratio, the versed sine will be augmented in the duplicate of that ratio (by Cor. 2 and 3, Lem. XI.), and therefore is as the force and the square of the time. Subduct on both sides the duplicate ratio of the time, and the force will be as the versed sine directly, and the square of the time inversely. Q.E.D.
And the same thing may also be easily demonstrated by Corol. 4, Lem. X.
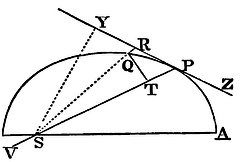
Cor. 1. If a body P revolving about the
centre S describes a curve line APQ, which a right line ZPR touches in
any point P; and from any other point Q of the curve, QR is drawn
parallel to the distance SP, meeting the tangent in R; and QT is drawn
perpendicular to the distance SP; the centripetal force will be
reciprocally as the solid SP2
x QT2
QR, if the solid be taken of that magnitude which it
ultimately acquires when the points P and Q coincide. For QR is equal
to the versed sine of double the arc QP, whose middle is P: and double
the triangle SQP, or SP x QT is
proportional to the time in which that double arc is described; and
therefore may be used for the exponent of the time.
Cor. 2. By a like reasoning, the centripetal
force is reciprocally as the solid SY2
x QP2
QR; if SY is a perpendicular from the centre of force on PR
the tangent of the orbit. For the rectangles SY x
QP and SP x QT are equal.
Cor. 3. If the orbit
is either a circle, or touches or cuts a circle concentrically, that
is, contains with a circle the least angle of contact or section,
having the same curvature and the same radius of curvature at the
point P; and if PV be a chord of this circle, drawn from the body
through the centre of force; the centripetal force will be
reciprocally as the solid SP2 x PV.
For PV is QP2
QR.
Cor. 4. The same things being supposed, the centripetal force is as the square of the velocity directly, and that chord inversely. For the velocity is reciprocally as the perpendicular SY, by Cor. 1. Prop. I.
Cor. 5. Hence if any curvilinear figure APQ
is given, and therein a point S is also given, to which a centripetal
force is perpetually directed, that law of centripetal force may be
found, by which the body P will be continually drawn back from a
rectilinear course, and being detained in the perimeter of that
figure, will describe the same by a perpetual revolution. That is, we
are to find, by computation, either the solid
SP2 x QT2
QR or the solid SP2 x PV,
reciprocally proportional to this force. Examples of this we shall
give in the following Problems.
Proposition vii. Problem ii.
If a body revolves in the circumference of a circle; it is proposed to find the law of centripetal force directed to any given point.
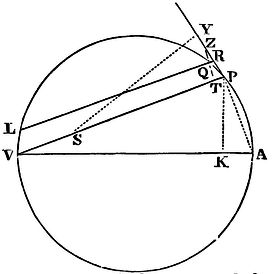
Let VQPA be the circumference of the circle; S the given point to
which as to a centre the force tends; P the body moving in the
circumference; Q the next place into which it is to move; and PRZ the
tangent of the circle at the preceding place. Through the point S draw
the chord PV, and the diameter VA of the circle: join AP, and draw QT
perpendicular to SP, which produced, may meet the tangent PR in Z; and
lastly, through the point Q, draw LR parallel to SP, meeting the
circle in L, and the tangent PZ in R. And, because of the similar
triangles ZQR, ZTP, VPA, we shall have RP², that is, QRL to QT² as AV²
to PV². And therefore
QRL x SP2
AV2 is equal to QT². Multiply those equals by
SP2
QR,
and the points P and Q coinciding, for RL write PV; then we shall have
SP2
x PV3
AV2 = SP2
x QT2
QR. And therefore (by Cor 1 and 5, Prop. VI.)
the centripetal force is reciprocally as
SP2 x PV3
AV2; that is (because
AV² is given), reciprocally as the square of the distance or altitude
SP, and the cube of the chord PV conjunctly. Q.E.I.
The same otherwise.
On the tangent PR produced let fall the perpendicular SY; and
(because of the similar triangles SYP, VPA), we shall have AV to PV as
SP to SY, and therefore SP
x PV
AV = SY, and
SP2 x PV3
AV2 = SY2
x PV. And therefore (by Corol. 3 and 5, Prop. VI),
the centripetal force is reciprocally as SP2
x PV3
AV2; that is (because AV
is given), reciprocally as SP2 x PV3.
Q.E.I.
Cor. 1. Hence if the given point S, to which the centripetal force always tends, is placed in the circumference of the circle, as at V, the centripetal force will be reciprocally as the quadrato-cube (or fifth power) of the altitude SP.

Cor. 2. The force by which the body P in the
circle APTV revolves about the centre of force S is to the force by
which the same body P may revolve in the same circle, and in the same
periodic time, about any other centre of force R, as RP2
x SP to the cube of the right line SG, which, from the first
centre of force S is drawn parallel to the distance PR of the body
from the second centre of force R, meeting the tangent PG of the orbit
in G. For by the construction of this Proposition, the former force is
to the latter as RP2 x PT3
to SP2 x PV3 ; that
is, as SP x RP2 to
SP3 x PV3
PT3; or (because of the
similar triangles PSG, TPV) to SG³.
Cor. 3. The force by which the body P in any orbit revolves about the centre of force S, is to the force by which the same body may revolve in the same orbit, and the same periodic time, about any other centre of force R, as the solid SP x RP2, contained under the distance of the body from the first centre of force S, and the square of its distance from the second centre of force R, to the cube of the right line SG, drawn from the first centre of the force S, parallel to the distance RP of the body from the second centre of force R, meeting the tangent PG of the orbit in G. For the force in this orbit at any point P is the same as in a circle of the same curvature.
Proposition viii. Problem iii.
If a body moves in the semi-circumference PQA; it is proposed to find the law of the centripetal force tending to a point S, so remote, that all the lines PS, RS drawn thereto, may be taken for parallels.
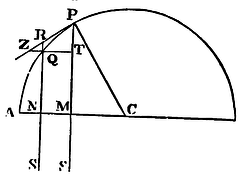
From C, the centre of the semi-circle, let the semi-diameter CA he
drawn, cutting the parallels at right angles in M and N, and join CP.
Because of the similar triangles CPM, PZT, and RZQ, we shall have CP²
to PM² as PR² to QT²; and, from the nature of the circle, PR² is equal
to the rectangle QR x (RN + QN), or, the
points P, Q, coinciding, to the rectangle QR x 2PM.
Therefore CP² is to PM² as QR x 2PM to QT²;
and QT2
QR = 2PM3
CP2, and
QT2 x SP2
QR = 2PM3 x
SP2
CP2. And therefore (by Corol. 1 and 5;
Prop. VI.), the centripetal force is reciprocally as
2PM3 x SP2
CP2; that is (neglecting the given ratio
2SP2
CP2 ), reciprocally as PM³. Q.E.I.
And the same thing is likewise easily inferred from the preceding Proposition.
Scholium.
And by a like reasoning, a body will be moved in an ellipsis, or even in an hyperbola, or parabola, by a centripetal force which is reciprocally ae the cube of the ordinate directed to an infinitely remote centre of force.
Proposition ix. Problem iv.
If a body revolves in a spiral PQS, cutting all the radii SP, SQ, &c., in a given angle; it is proposed to find the law of the centripetal force tending to the centre of that spiral.
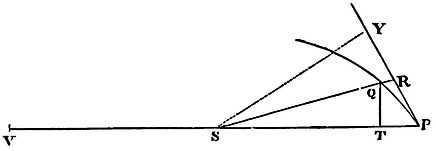
Suppose the indefinitely small angle PSQ to be given; because, then,
all the angles are given, the figure SPRQT will be given in specie.
Therefore the ratio QT
QR is also given, and QT2
QR is as QT, that is (because the figure is given in specie),
as SP. But if the angle PSQ is any way changed, the right line QR,
subtending the angle of contact QPR (by Lemma
XI) will be changed in the duplicate ratio of PR or QT. Therefore the
ratio QT2
QR remains the same as before, that is, as SP. And
QT2 x SP2
QR is as SP³, and therefore (by Corol. 1 and 5, Prop. VI) the
centripetal force is reciprocally as the cube of the distance SP.
Q.E.I.
The same otherwise.
The perpendicular SY let fall upon the tangent, and the chord PV of the circle concentrically cutting the spiral, are in given ratios to the height SP; and therefore SP³ is as SY² x PV, that is (by Corol. 3 and 5, Prop. VI) reciprocally as the centripetal force.
Lemma xii.
All parallelograms circumscribed about any conjugate diameters of a given ellipsis or hyperbola are equal among themselves.
This is demonstrated by the writers on the conic sections.
Proposition x. Problem V.
If a body revolves in an ellipsis; it is proposed to find the law of the centripetal force tending to the centre of the ellipsis.
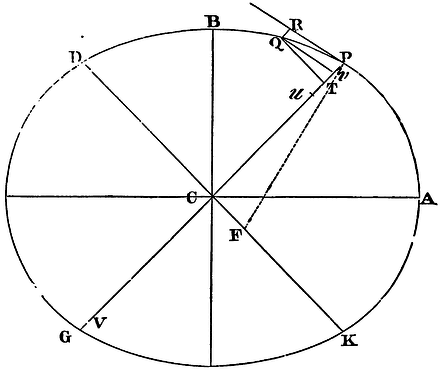
Suppose CA, CB to be semi-axes of the ellipsis; GP, DK, conjugate
diameters; PF, QT perpendiculars to those diameters; Qv an
ordinate to the diameter GP; and if the parallelogram QvPR be
completed, then (by the properties of the conic sections) the
rectangle PvG will be to Qv² as PC² to CD²; and
(because of the similar triangles QvT, PCF), Qv² to
QT² as PC² to PF²; and, by composition, the ratio of PvG to
QT² is compounded of the ratio of PC² to CD², and of the ratio of PC²
to PF², that is, vG to QT2
Pv as PC² to
CD2 x PF2
PC2. Put QR for Pv,
and (by Lem. XII) BC x CA for CD x PF; also (the points P and Q
coinciding) 2PC for vG; and multiplying the
extremes and means together, we shall have QT2
x PC2
QR equal to 2BC2
x CA2
PC. Therefore (by Cor. 5, Prop. VI),
the centripetal force is reciprocally as 2BC2
x CA2
PC; that is (because 2BC2
x CA2 is given), reciprocally as
1
PC; that is, directly as the distance
PC. QEI.
The same otherwise.
In the right line PG on the other side of the point T, take the point
u so that Tu may be equal to Tv; then take
uV, such as shall be to vG as DC² to PC². And
because Qv² is to PvG as DC² to PC² (by the conic
sections), we shall have QV2=Pv x uV.
Add the rectangle uPv to both sides, and the square
of the chord of the arc PQ will be equal to the rectangle VPv;
and therefore a circle which touches the conic section in P, and
passes through the point Q, will pass also through the point V. Now
let the points P and Q meet, and the ratio of uV to vG,
which is the same with the ratio of DC² to PC², will become the ratio
of PV to PG, or PV to 2PC; and therefore PV will be equal to
2DC2
PC. And therefore the force by which
the body P revolves in the ellipsis will be reciprocally as
2DC2
PC x PF2 (by Cor. 3, Prop
VI); that is (because 2DC² x PF² is given) directly as PC.
Q.E.I.
Cor. 1. And therefore the force is as the distance of the body from the centre of the ellipsis; and, vice versa, if the force is as the distance, the body will move in an ellipsis whose centre coincides with the centre of force, or perhaps in a circle into which the ellipsis may degenerate.
Cor. 2. And the periodic times of the revolutions made in all ellipses whatsoever about the same centre will be equal. For those times in similar ellipses will be equal (by Corol. 3 and 8, Prop. IV); but in ellipses that have their greater axis common, they are one to another as the whole areas of the ellipses directly, and the parts of the areas described in the same time inversely; that is, as the lesser axes directly, and the velocities of the bodies in their principal vertices inversely; that is, as those lesser axes directly, and the ordinates to the same point of the common axes inversely; and therefore (because of the equality of the direct and inverse ratios) in the ratio of equality.
Scholium.
If the ellipsis, by having its centre removed to an infinite distance, de generates into a parabola, the body will move in this parabola; and the force, now tending to a centre infinitely remote, will become equable. Which is Galileo's theorem. And if the parabolic section of the cone (by changing the inclination of the cutting plane to the cone) degenerates into an hyperbola, the body will move in the perimeter of this hyperbola, having its centripetal force changed into a centrifugal force. And in like manner as in the circle, or in the ellipsis, if the forces are directed to the centre of the figure placed in the abscissa, those forces by increasing or diminishing the ordinates in any given ratio; or even by changing the angle of the inclination of the ordinates to the abscissa, are always augmented or diminished in the ratio of the distances from the centre; provided the periodic times remain equal; so also in all figures whatsoever, if the ordinates are augmented or diminished in any given ratio, or their inclination is any way changed, the periodic time remaining the same, the forces directed to any centre placed in the abscissa are in the several ordinates augmented or diminished in the ratio of the distances from the centre.