Section ix.
Of the circular motion of fluids.
Hypothesis.
The resistance arising from the want of lubricity in the parts of a fluid, is, caeteris paribus, proportional to the velocity with which the parts of the fluid are separated from each other.
Proposition li. Theorem xxxix.
If a solid cylinder infinitely long, in an uniform and infinite fluid, revolve with an uniform motion about an axis given in position, and the fluid be forced round by only this impulse of the cylinder, and every part of the fluid persevere uniformly in its motion; I say, that the periodic times of the parts of the fluid are as their distances from the axis of the cylinder.
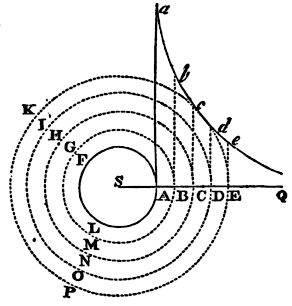
Let AFL be a cylinder turning uniformly about the axis S, and let the concentric circles BGM, CHN, DIO, EKP, &c., divide the fluid into innumerable concentric cylindric solid orbs of the same thickness. Then, because the fluid is homogeneous, the impressions which the contiguous orbs make upon each other mutually will be (by the Hypothesis) as their translations from each other, and as the contiguous superficies upon which the impressions are made. If the impression made upon any orb be greater or less on its concave than on its convex side, the stronger impression will prevail, and will either accelerate or retard the motion of the orb, according as it agrees with, or is contrary to, the motion of the same. Therefore, that every orb may persevere uniformly in its motion, the impressions made on both sides must be equal and their directions contrary. Therefore since the impressions are as the contiguous superficies, and as their translations from one another, the translations will be inversely as the superficies, that is, inversely as the distances of the superficies from the axis. But the differences of the angular motions about the axis are as those translations applied to the distances, or as the translations directly and the distances inversely; that is, joining these ratios together, as the squares of the distances inversely. Therefore if there be erected the lines Aa, Bb, Cc, Dd, Ee, &c., perpendicular to the several parts of he infinite right line SABCDEQ, and reciprocally proportional to the squares of SA, SB, SC, SD, SE, &c., and through the extremities of those perpendiculars there be supposed to pass an hyperbolic curve, the sums of the differences, that is, the whole angular motions, will be as the correspondent sums of the lines Aa, Bb, Cc, Dd, Ee, that is (if to constitute a medium uniformly fluid the number of the orbs be increased and their breadth diminished in infinitum), as the hyperbolic areas AaQ, BbQ, CcQ, DdQ, EeQ, &c., analogous to the sums; and the times, reciprocally proportional to the angular motions, will be also reciprocally proportional to those areas. Therefore the periodic time of any particle as D, is reciprocally as the area DdQ, that is (as appears from the known methods of quadratures of curves), directly as the distance SD. Q.E.D.
Cor. 1. Hence the angular motions of the particles of the fluid are reciprocally as their distances from the axis of the cylinder, and the absolute velocities are equal.
Cor. 2. If a fluid be contained in a cylindric vessel of an infinite length, and contain another cylinder within, and both the cylinders revolve about one common axis, and the times of their revolutions be as their semi-diameters, and every part of the fluid perseveres in its motion, the periodic times of the several parts will be as the distances from the axis of the cylinders.
Cor. 3. If there be added or taken away any common quantity of angular motion from the cylinder and fluid moving in this manner; yet because this new motion will not alter the mutual attrition of the parts of the fluid, the motion of the parts among themselves will not be changed; for the translations of the parts from one another depend upon the attrition. Any part will persevere in that motion, which, by the attrition made on both sides with contrary directions, is no more accelerated than it is retarded.
Cor. 4. Therefore if there be taken away from this whole system of the cylinders and the fluid all the angular motion of the outward cylinder, we shall have the motion of the fluid in a quiescent cylinder.
Cor. 5. Therefore if the fluid and outward cylinder are at rest, and the inward cylinder revolve uniformly, there will be communicated a circular motion to the fluid, which will be propagated by degrees through the whole fluid; and will go on continually increasing, till such time as the several parts of the fluid acquire the motion determined in Cor. 4.
Cor. 6. And because the fluid endeavours to propagate its motion still farther, its impulse will carry the outmost cylinder also about with it, unless the cylinder be violently detained; and accelerate its motion till the periodic times of both cylinders become equal among themselves. But if the outward cylinder be violently detained, it will make an effort to retard the motion of the fluid; and unless the inward cylinder preserve that motion by means of some external force impressed thereon, it will make it cease by degrees.
All these things will be found true by making the experiment in deep standing water.
Proposition lii. Theorem xl.
If a solid sphere, in an uniform and infinite fluid, revolves about an axis given in position, with an uniform motion, and the fluid be forced round by only this impulse of the sphere; and every part of the fluid perseveres uniformly in its motion; I say, that the periodic times of the parts of the fluid are as the squares of their distances from the centre of the sphere.

Case 1. Let AFL be a sphere turning uniformly about the axis S, and let the concentric circles BGM, CHN, DIO, EKP, &c., divide the fluid into innumerable concentric orbs of the same thickness. Suppose those orbs to be solid; and, because the fluid is homogeneous, the impressions which the contiguous orbs make one upon another will be (by the supposition) as their translations from one another, and the contiguous superficies upon which the impressions are made. If the impression upon any orb be greater or less upon its concave than upon its convex side, the more forcible impression will prevail, and will either accelerate or retard the velocity of the orb, according as it is directed with a conspiring or contrary motion to that of the orb. Therefore that every orb may persevere uniformly in its motion, it is necessary that the impressions made upon both sides of the orb should be equal, and have contrary directions. Therefore since the impressions are as the contiguous superficies, and as their translations from one another, the translations will be inversely as the superficies, that is, inversely as the squares of the distances of the superficies from the centre. But the differences of the angular motions about the axis are as those translations applied to the distances, or as the translations directly and the distances inversely; that is, by compounding those ratios, as the cubes of the distances inversely. Therefore if upon the several parts of the infinite right line SABCDEQ there be erected the perpendiculars Aa, Bb, Cc, Dd, Ee, &c., reciprocally proportional to the cubes of SA, SB, SC, SD, SE, &c., the sums of the differences, that is, the whole angular motions will be as the corresponding sums of the lines Aa, Bb, Cc, Dd, Ee, &c., that is (if to constitute an uniformly fluid medium the number of the orbs be increased and their thickness diminished in infinitum), as the hyperbolic areas AaQ, BbQ, CcQ, DdQ, EeQ, &c., analogous to the sums; and the periodic times being reciprocally proportional to the angular motions, will be also reciprocally proportional to those areas. Therefore the periodic time of any orb DIO is reciprocally as the area DdQ, that is (by the known methods of quadratures), directly as the square of the distance SD. Which was first to be demonstrated.
Case 2. From the centre of the sphere let there be drawn a great number of indefinite right lines, making given angles with the axis, exceeding one another by equal differences; and, by these lines revolving about the axis, conceive the orbs to be cut into innumerable annuli; then will every annulus have four annuli contiguous to it, that is, one on its inside, one on its outside, and two on each hand. Now each of these annuli cannot be impelled equally and with contrary directions by the attrition of the interior and exterior annuli, unless the motion be communicated according to the law which we demonstrated in Case 1. This appears from that demonstration. And therefore any series of annuli, taken in any right line extending itself in infinitum from the globe, will move according to the law of Case 1, except we should imagine it hindered by the attrition of the annuli on each side of it. But now in a motion, according to this law, no such is, and therefore cannot be, any obstacle to the motions persevering according to that law. If annuli at equal distances from the centre revolve either more swiftly or more slowly near the poles than near the ecliptic, they will be accelerated if slow, and retarded if swift, by their mutual attrition; and so the periodic times will continually approach to equality, according to the law of Case 1. Therefore this attrition will not at all hinder the motion from going on according to the law of Case 1, and therefore that law will take place; that is, the periodic times of the several annuli will be as the squares of their distances from the centre of the globe. Which was to be demonstrated in the second place.
Case 3. Let now every annulus be divided by transverse sections into innumerable particles constituting a substance absolutely and uniformly fluid; and because these sections do not at all respect the law of circular motion, but only serve to produce a fluid substance, the law of circular motion will continue the same as before. All the very small annuli will either not at all change their asperity and force of mutual attrition upon account of these sections, or else they will change the same equally. Therefore the proportion of the causes remaining the same, the proportion of the effects will remain the same also; that is, the proportion of the motions and the periodic times. Q.E.D. But now as the circular motion, and the centrifugal force thence arising, is greater at the ecliptic than at the poles, there must be some cause operating to retain the several particles in their circles; otherwise the matter that is at the ecliptic will always recede from the centre, and come round about to the poles by the outside of the vortex, and from thence return by the axis to the ecliptic with a perpetual circulation.
Cor. 1. Hence the angular motions of the parts of the fluid about the axis of the globe are reciprocally as the squares of the distances from the centre of the globe, and the absolute velocities are reciprocally as the same squares applied to the distances from the axis.
Cor. 2. If a globe revolve with a uniform motion about an axis of a given position in a similar and infinite quiescent fluid with an uniform motion, it will communicate a whirling motion to the fluid like that of a vortex, and that motion will by degrees be propagated onward in infinitum; and this motion will be increased, continually in every part of the fluid, till the periodical times of the several parts become as the squares of the distances from the centre of the globe.
Cor. 3. Because the inward parts of the vortex are by reason of their greater velocity continually pressing upon and driving forward the external parts, and by that action are perpetually communicating motion to them, and at the same time those exterior parts communicate the same quantity of motion to those that lie still beyond them, and by this action preserve the quantity of their motion continually unchanged, it is plain that the motion is perpetually transferred from the centre to the circumference of the vortex, till it is quite swallowed up and lost in the boundless extent of that circumference. The matter between any two spherical superficies concentrical to the vortex will never be accelerated; because that matter will be always transferring the motion it receives from the matter nearer the centre to that matter which lies nearer the circumference.
Cor. 4. Therefore, in order to continue a vortex in the same state of motion, some active principle is required from which the globe may receive continually the same quantity of motion which it is always communicating to the matter of the vortex. Without such a principle it will undoubtedly come to pass that the globe and the inward parts of the vortex, being always propagating their motion to the outward parts, and not receiving any new motion, will gradually move slower and slower, and at last be carried round no longer.
Cor. 5. If another globe should be swimming in the same vortex at a certain distance from its centre, and in the mean time by some force revolve constantly about an axis of a given inclination, the motion of this globe will drive the fluid round after the manner of a vortex; and at first this new and small vortex will revolve with its globe about the centre of the other; and in the mean time its motion will creep on farther and farther, and by degrees be propagated in infinitum, after the manner of the first vortex. And for the same reason that the globe of the new vortex was carried about before by the motion of the other vortex, the globe of this other will be carried about by the motion of this new vortex, so that the two globes will revolve about some intermediate point, and by reason of that circular motion mutually fly from each other, unless some force restrains them. Afterward, if the constantly impressed forces, by which the globes persevere in their motions, should cease, and every thing be left to act according to the laws of mechanics, the motion of the globes will languish by degrees (for the reason assigned in Cor. 3 and 4), and the vortices at last will quite stand still.
Cor. 6. If several globes in given places should constantly revolve with determined velocities about axes given in position, there would arise from them as many vortices going on in infinitum. For upon the same account that any one globe propagates its motion in infinitum, each globe apart will propagate its own motion in infinitum also; so that every part of the infinite fluid will be agitated with a motion resulting from the actions of all the globes. Therefore the vortices will not be confined by any certain limits, but by degrees run mutually into each other; and by the mutual actions of the vortices on each other, the globes will be perpetually moved from their places, as was shewn in the last Corollary; neither can they possibly keep any certain position among themselves, unless some force restrains them. But if those forces, which are constantly impressed upon the globes to continue these motions, should cease, the matter (for the reason assigned in Cor. 3 and 4) will gradually stop, and cease to move in vortices.
Cor. 7. If a similar fluid be inclosed in a spherical vessel, and, by the uniform rotation of a globe in its centre, is driven round in a vortex; and the globe and vessel revolve the same way about the same axis, and their periodical times be as the squares of the semi-diameters; the parts of the fluid will not go on in their motions without acceleration or retardation, till their periodical times are as the squares of their distances from the centre of the vortex. No constitution of a vortex can be permanent but this.
Cor. 8. If the vessel, the inclosed fluid, and the globe, retain this motion, and revolve besides with a common angular motion about any given axis, because the mutual attrition of the parts of the fluid is not changed by this motion, the motions of the parts among each other will not be changed; for the translations of the parts among themselves depend upon this attrition. Any part will persevere in that motion in which its attrition on one side retards it just as much as its attrition on the other side accelerates it.
Cor. 9. Therefore if the vessel be quiescent, and the motion of the globe be given, the motion of the fluid will be given. For conceive a plane to pass through the axis of the globe, and to revolve with a contrary motion; and suppose the sum of the time of this revolution and of the revolution of the globe to be to the time of the revolution of the globe as the square of the semi-diameter of the vessel to the square of the semi-diameter of the globe; and the periodic times of the parts of the fluid in respect of this plane will be as the squares of their distances from the centre of the globe.
Cor. 10. Therefore if the vessel move about the same axis with the globe, or with a given velocity about a different one, the motion of the fluid will be given. For if from the whole system we take away the angular motion of the vessel, all the motions will remain the same among themselves as before, by Cor. 8, and those motions will be given by Cor. 9.
Cor. 11. If the vessel and the fluid are quiescent, and the globe revolves with an uniform motion, that motion will be propagated by degrees through the whole fluid to the vessel, and the vessel will be carried round by it, unless violently detained; and the fluid and the vessel will be continually accelerated till their periodic times become equal to the periodic times of the globe. If the vessel be either withheld by some force, or revolve with any constant and uniform motion, the medium will come by little and little to the state of motion defined in Cor. 8, 9, 10, nor will it ever persevere in any other state. But if then the forces, by which the globe and vessel revolve with certain motions, should cease, and the whole system be left to act according to the mechanical laws, the vessel and globe, by means of the intervening fluid, will act upon each other, and will continue to propagate their motions through the fluid to each other, till their periodic times become equal among themselves, and the whole system revolves together like one solid body.
Scholium.
In all these reasonings I suppose the fluid to consist of matter of uniform density and fluidity; I mean, that the fluid is such, that a globe placed any where therein may propagate with the same motion of its own, at distances from itself continually equal, similar and equal motions in the fluid in the same interval of time. The matter by its circular motion endeavours to recede from the axis of the vortex, and therefore presses all the matter that lies beyond. This pressure makes the attrition greater, and the separation of the parts more difficult; and by consequence diminishes the fluidity of the matter. Again; if the parts of the fluid are in any one place denser or larger than in the others, the fluidity will be less in that place, because there are fewer superficies where the parts can be separated from each other. In these cases I suppose the defect of the fluidity to be supplied by the smoothness or softness of the parts, or some other condition; otherwise the matter where it is less fluid will cohere more, and be more sluggish, and therefore will receive the motion more slowly, and propagate it farther than agrees with the ratio above assigned. If the vessel be not spherical, the particles will move in lines not circular, but answering to the figure of the vessel; and the periodic times will be nearly as the squares of the mean distances from the centre. In the parts between the centre and the circumference the motions will be slower where the spaces are wide, and swifter where narrow; but yet the particles will not tend to the circumference at all the more for their greater swiftness; for they then describe arcs of less curvity, and the conatus of receding from the centre is as much diminished by the diminution of this curvature as it is augmented by the increase of the velocity. As they go out of narrow into wide spaces, they recede a little farther from the centre, but in doing so are retarded; and when they come out of wide into narrow spaces, they are again accelerated; and so each particle is retarded and accelerated by turns for ever. These things will come to pass in a rigid vessel; for the state of vortices in an infinite fluid is known by Cor. 6 of this Proposition.
I have endeavoured in this Proposition to investigate the properties of vortices, that I might find whether the celestial phenomena can be explained by them; for the phenomenon is this, that the periodic times of the planets revolving about Jupiter are in the sesquiplicate ratio of their distances from Jupiter's centre; and the same rule obtains also among the planets that revolve about the sun. And these rules obtain also with the greatest accuracy, as far as has been yet discovered by astronomical observation. Therefore if those planets are carried round in vortices revolving about Jupiter and the sun, the vortices must revolve according to that law. But here we found the periodic times of the parts of the vortex to be in the duplicate ratio of the distances from the centre of motion; and this ratio cannot be diminished and reduced to the sesquiplicate, unless either the matter of the vortex be more fluid the farther it is from the centre, or the resistance arising from the want of lubricity in the parts of the fluid should, as the velocity with which the parts of the fluid are separated goes on increasing, be augmented with it in a greater ratio than that in which the velocity increases. But neither of these suppositions seem reasonable. The more gross and less fluid parts will tend to the circumference, unless they are heavy towards the centre. And though, for the sake of demonstration, I proposed, at the beginning of this Section, an Hypothesis that the resistance is proportional to the velocity, nevertheless, it is in truth probable that the resistance is in a less ratio than that of the velocity; which granted, the periodic times of the parts of the vortex will be in a greater than the duplicate ratio of the distances from its centre. If, as some think, the vortices move more swiftly near the centre, then slower to a certain limit, then again swifter near the circumference, certainty neither the sesquiplicate, nor any other certain and determinate ratio, can obtain in them. Let philosophers then see how that phenomenon of the sesquiplicate ratio can be accounted for by vortices.
Proposition liii. Theorem xli.
Bodies carried about in a vortex, and returning in the same orb, are of the same density with the vortex, and are moved according to the same law with the parts of the vortex, as to velocity and direction of motion.
For if any small part of the vortex, whose particles or physical points preserve a given situation among each other, be supposed to be congealed, this particle will move according to the same law as before, since no change is made either in its density, vis insita, or figure. And again; if a congealed or solid part of the vortex be of the same density with the rest of the vortex, and be resolved into a fluid, this will move according to the same law as before, except in so far as its particles, now become fluid, may be moved among themselves. Neglect, therefore, the motion of the particles among themselves as not at all concerning the progressive motion of the whole, and the motion of the whole will be the same as before. But this motion will be the same with the motion of other parts of the vortex at equal distances from the centre; because the solid, now resolved into a fluid, is become perfectly like to the other parts of the vortex. Therefore a solid, if it be of the same density with the matter of the vortex, will move with the same motion as the parts thereof, being relatively at rest in the matter that surrounds it. If it be more dense, it will endeavour more than before to recede from the centre; and therefore overcoming that force of the vortex, by which, being, as it were, kept in equilibrio, it was retained in its orbit, it will recede from the centre, and in its revolution describe a spiral, returning no longer into the same orbit. And, by the same argument, if it be more rare, it will approach to the centre. Therefore it can never continually go round in the same orbit, unless it be of the same density with the fluid. But we have shewn in that case that it would revolve according to the same law with those parts of the fluid that are at the same or equal distances from the centre of the vortex.
Cor. 1. Therefore a solid revolving in a vortex, and continually going round in the same orbit, is relatively quiescent in the fluid that carries it.
Cor. 2. And if the vortex be of an uniform density, the same body may revolve at any distance from the centre of the vortex.
Scholium.
Hence it is manifest that the planets are not carried round in
corporeal vortices; for, according to the Copernican
hypothesis, the planets going
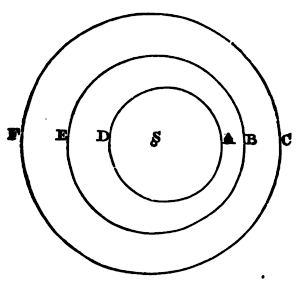 round the sun revolve in ellipses, having the sun in their common
focus; and by radii drawn to the sun describe areas proportional to
the times. But now the parts of a vortex can never revolve with such a
motion. Let AD, BE, CF, represent three orbits described about the sun
S, of which let the utmost circle CF be concentric to the sun; and let
the aphelia of the two innermost be A, B; and their perihelia D, E.
Therefore a body revolving in the orb CF, describing, by a radius
drawn to the sun, areas proportional to the times, will move with an
uniform motion. And, according to the laws of astronomy, the body
revolving in the orb BE will move slower in its aphelion B, and
swifter in its perihelion E; whereas, according to the laws of
mechanics, the matter of the vortex ought to move more swiftly in the
narrow space between A and C than in the wide space between D and F;
that is, more swiftly in the aphelion than in the perihelion. Now
these two conclusions contradict each other. So at the beginning of
the sign of Virgo, where the aphelion of Mars is at present, the
distance between the orbits of Mars and Venus is to the distance
between the same orbits, at the beginning of the sign of Pisces, as
about 3 to 2; and therefore the matter of the vortex between those
orbits ought to be swifter at the beginning of Pisces than at the
beginning of Virgo in the ratio of 3 to 2; for the narrower the space
is through which the same quantity of matter passes in the same time
of one revolution, the greater will be the velocity with which it
passes through it. Therefore if the earth being relatively at rest in
this celestial matter should be carried round by it, and revolve
together with it about the sun, the velocity of the earth at the
beginning of Pisces would be to its velocity at the beginning of Virgo
in a sesquialteral ratio. Therefore the sun's apparent diurnal motion
at the beginning of Virgo ought to be above 70 minutes, and at the
beginning of Pisces less than 48 minutes; whereas, on the contrary,
that apparent motion of the sun is really greater at the beginning of
Pisces than at the beginning of Virgo, as experience testifies; and
therefore the earth is swifter at the beginning of Virgo than at the
beginning of Pisces; so that the hypothesis of vortices is utterly
irreconcileable with astronomical phaenomena, and rather serves to
perplex than explain the heavenly motions. How these motions are
performed in free spaces without vortices, may be understood by the
first Book; and I shall now more fully treat of it in the following
Book.
round the sun revolve in ellipses, having the sun in their common
focus; and by radii drawn to the sun describe areas proportional to
the times. But now the parts of a vortex can never revolve with such a
motion. Let AD, BE, CF, represent three orbits described about the sun
S, of which let the utmost circle CF be concentric to the sun; and let
the aphelia of the two innermost be A, B; and their perihelia D, E.
Therefore a body revolving in the orb CF, describing, by a radius
drawn to the sun, areas proportional to the times, will move with an
uniform motion. And, according to the laws of astronomy, the body
revolving in the orb BE will move slower in its aphelion B, and
swifter in its perihelion E; whereas, according to the laws of
mechanics, the matter of the vortex ought to move more swiftly in the
narrow space between A and C than in the wide space between D and F;
that is, more swiftly in the aphelion than in the perihelion. Now
these two conclusions contradict each other. So at the beginning of
the sign of Virgo, where the aphelion of Mars is at present, the
distance between the orbits of Mars and Venus is to the distance
between the same orbits, at the beginning of the sign of Pisces, as
about 3 to 2; and therefore the matter of the vortex between those
orbits ought to be swifter at the beginning of Pisces than at the
beginning of Virgo in the ratio of 3 to 2; for the narrower the space
is through which the same quantity of matter passes in the same time
of one revolution, the greater will be the velocity with which it
passes through it. Therefore if the earth being relatively at rest in
this celestial matter should be carried round by it, and revolve
together with it about the sun, the velocity of the earth at the
beginning of Pisces would be to its velocity at the beginning of Virgo
in a sesquialteral ratio. Therefore the sun's apparent diurnal motion
at the beginning of Virgo ought to be above 70 minutes, and at the
beginning of Pisces less than 48 minutes; whereas, on the contrary,
that apparent motion of the sun is really greater at the beginning of
Pisces than at the beginning of Virgo, as experience testifies; and
therefore the earth is swifter at the beginning of Virgo than at the
beginning of Pisces; so that the hypothesis of vortices is utterly
irreconcileable with astronomical phaenomena, and rather serves to
perplex than explain the heavenly motions. How these motions are
performed in free spaces without vortices, may be understood by the
first Book; and I shall now more fully treat of it in the following
Book.