Section viii.
Of motion propagated through fluids.
Proposition xli. Theorem xxxii.
A pressure is not propagated through a fluid in rectilinear directions unless where the particles of the fluid lie in a right line.
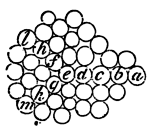
If the particles a, b, c, d, e, lie in a right line, the pressure may be indeed directly propagated from a to e; but then the particle e will urge the obliquely posited particles f and g obliquely, and those particles f and g will not sustain this pressure, unless they be supported by the particles h and k lying beyond them; but the particles that support them are also pressed by them; and those particles cannot sustain that pressure, without being supported by, and pressing upon, those particles that lie still farther, as l and m, and so on in infinitum. Therefore the pressure, as soon as it is propagated to particles that lie out of right lines, begins to deflect towards one hand and the other, and will be propagated obliquely in infinitum; and after it has begun to be propagated obliquely, if it reaches more distant particles lying out of the right line, it will deflect again on each hand and this it will do as often as it lights on particles that do not lie exactly in a right line. Q.E.D.
Cor. If any part of a pressure, propagated
through a fluid from a given point, be intercepted by any obstacle,
the remaining part, which is not intercepted, will deflect into the
spaces behind the obstacle. This may be demonstrated also after the
following manner. Let a pressure be propagated from the point A
towards any part, and, if it be possible, in rectilinear
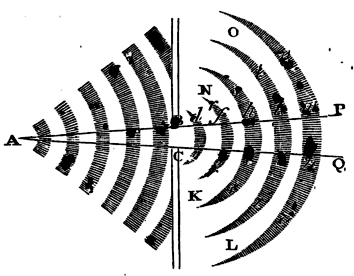 directions; and the obstacle NBCK being perforated in BC, let all the
pressure be intercepted but the coniform part APQ passing through the
circular hole BC. Let the cone APQ be divided into frustums by the
transverse plants, de, fg, hi. Then while the cone ABC,
propagating the pressure, urges the conic frustum degf
beyond it on the superficies de, and this frustum urges the
next frustum fgih on the superficies fg, and that
frustum urges a third frustum, and so in infinitum; it is
manifest (by the third Law) that the first frustum defg is,
by the re-action of the second frustum fghi, as much urged
and pressed on the superficies fg, as it urges and presses
that second frustum. Therefore the frustum degf is
compressed on both sides, that is, between the cone Ade and
the frustum fhig; and therefore (by Case 6, Prop. XIX)
cannot preserve its figure, unless it be compressed with the same
force on all sides. Therefore with the same force with which it is
pressed on the superficies de, fg, it will endeavour to
break forth at the sides df, eg; and there (being not in the
least tenacious or hard, but perfectly fluid) it will run out,
expanding itself, unless there be an ambient fluid opposing that
endeavour. Therefore, by the effort it makes to run out, it will press
the ambient fluid, at its sides df, eg, with the same force
that it does the frustum fghi; and therefore, the pressure
will be propagated as much from the sides df, eg, into the
spaces NO, KL this way and that way, as it is propagated from the
superficies fg towards PQ. Q.E.D.
directions; and the obstacle NBCK being perforated in BC, let all the
pressure be intercepted but the coniform part APQ passing through the
circular hole BC. Let the cone APQ be divided into frustums by the
transverse plants, de, fg, hi. Then while the cone ABC,
propagating the pressure, urges the conic frustum degf
beyond it on the superficies de, and this frustum urges the
next frustum fgih on the superficies fg, and that
frustum urges a third frustum, and so in infinitum; it is
manifest (by the third Law) that the first frustum defg is,
by the re-action of the second frustum fghi, as much urged
and pressed on the superficies fg, as it urges and presses
that second frustum. Therefore the frustum degf is
compressed on both sides, that is, between the cone Ade and
the frustum fhig; and therefore (by Case 6, Prop. XIX)
cannot preserve its figure, unless it be compressed with the same
force on all sides. Therefore with the same force with which it is
pressed on the superficies de, fg, it will endeavour to
break forth at the sides df, eg; and there (being not in the
least tenacious or hard, but perfectly fluid) it will run out,
expanding itself, unless there be an ambient fluid opposing that
endeavour. Therefore, by the effort it makes to run out, it will press
the ambient fluid, at its sides df, eg, with the same force
that it does the frustum fghi; and therefore, the pressure
will be propagated as much from the sides df, eg, into the
spaces NO, KL this way and that way, as it is propagated from the
superficies fg towards PQ. Q.E.D.
Proposition xlii. Theorem xxxiii.
All motion propagated through a fluid diverges from a rectilinear progress into the unmoved spaces.

Case 1. Let a motion be propagated from the point A through the hole BC, and, if it be possible, let it proceed in the conic space BCQP according to right lines diverging from the point A. And let us first suppose this motion to be that of waves in the surface of standing water; and let de, fg, hi, kl, &c., be the tops of the several waves, divided from each other by as many intermediate valleys or hollows. Then, because the water in the ridges of the waves is higher than in the unmoved parts of the fluid KL, NO, it will run down from off the tops of those ridges, e, g, i, l, &c., d, f, h, k, &c., this way and that way towards KL and NO; and because the water is more depressed in the hollows of the waves than in the unmoved parts of the fluid KL, NO, it will run down into those hollows out of those unmoved parts. By the first deflux the ridges of the waves will dilate themselves this way and that way, and be propagated towards KL and NO. And because the motion of the waves from A towards PQ is carried on by a continual deflux from the ridges of the waves into the hollows next to them, and therefore cannot be swifter than in proportion to the celerity of the descent; and the descent of the water on each side towards KL and NO must be performed with the same velocity; it follows that the dilatation of the waves on each side towards KL and NO will be propagated with the same velocity as the waves themselves go forward with directly from A to PQ. And therefore the whole space this way and that way towards KL and NO will be filled by the dilated waves rfgr, shis, tklt, vmnv, &c. Q.E.D. That these things are so, any one may find by making the experiment in still water.
Case 2. Let us suppose that de, fg, hi, kl, mn, represent pulses successively propagated from the point A through an elastic medium. Conceive the pulses to be propagated by successive condensations and rarefactions of the medium, so that the densest part of every pulse may occupy a spherical superficies described about the centre A, and that equal intervals intervene between the successive pulses. Let the lines de, fg, hi, kl, &c., represent the densest parts of the pulses, propagated through the hole BC; and because the medium is denser there than in the spaces on either side towards KL and NO, it will dilate itself as well towards those spaces KL, NO, on each hand, as towards the rare intervals between the pulses; and thence the medium, becoming always more rare next the intervals, and more dense next the pulses, will partake of their motion. And because the progressive motion of the pulses arises from the perpetual relaxation of the denser parts towards the antecedent rare intervals; and since the pulses will relax themselves on each hand towards the quiescent parts of the medium KL, NO, with very near the same celerity; therefore the pulses will dilate themselves on all sides into the unmoved parts KL, NO, with almost the same celerity with which they are propagated directly from the centre A; and therefore will fill up the whole space KLON. Q.E.D. And we find the same by experience also in sounds which are heard through a mountain interposed; and, if they come into a chamber through the window, dilate themselves into all the parts of the room, and are heard in every corner; and not as reflected from the opposite walls, but directly propagated from the window, as far as our sense can judge.
Case 3 Let us suppose, lastly, that a motion of any kind is propagated from A through the hole BC. Then since the cause of this propagation is that the parts of the medium that are near the centre A disturb and agitate those which lie farther from it; and since the parts which are urged are fluid, and therefore recede every way towards those spaces where they are less pressed, they will by consequence recede towards all the parts of the quiescent medium; as well to the parts on each hand, as KL and NO, as to those right before, as PQ; and by this means all the motion, as soon as it has passed through the hole BC, will begin to dilate itself, and from thence, as from its principle and centre, will be propagated directly every way. Q.E.D.
Proposition xliii. Theorem xxxiv.
Every tremulous body in an elastic medium propagates the motion of the pulses on every side right forward; but in a non-elastic medium excites a circular motion.
Case. 1. The parts of the tremulous body, alternately going and returning, do in going urge and drive before them those parts of the medium that lie nearest, and by that impulse compress and condense them; and in returning suffer those compressed parts to recede again, and expand themselves. Therefore the parts of the medium that lie nearest to the tremulous body move to and fro by turns, in like manner as the parts of the tremulous body itself do; and for the same cause that the parts of this body agitate these parts of the medium, these parts, being agitated by like tremors, will in their turn agitate others next to themselves; and these others, agitated in like manner, will agitate those that lie beyond them, and so on in infinitum. And in the same manner as the first parts of the medium were condensed in going, and relaxed in returning, so will the other parts be condensed every time they go, and expand themselves every time they re turn. And therefore they will not be all going and all returning at the same instant (for in that case they would always preserve determined distances from each other, and there could be no alternate condensation and rarefaction); but since, in the places where they are condensed, they approach to, and, in the places where they are rarefied, recede from each other, therefore some of them will be going while others are returning; and so on in infinitum. The parts so going, and in their going condensed, are pulses, by reason of the progressive motion with which they strike obstacles in their way; and therefore the successive pulses produced by a tremulous body will be propagated in rectilinear directions; and that at nearly equal distances from each other, because of the equal intervals of time in which the body, by its several tremors produces the several pulses. And though the parts of the tremulous body go and return in some certain and determinate direction, yet the pulses propagated from thence through the medium will dilate themselves towards the sides, by the foregoing Proposition; and will be propagated on all sides from that tremulous body, as from a common centre, in superficies nearly spherical and concentrical. An example of this we have in waves excited by shaking a finger in water, which proceed not only forward and backward agreeably to the motion of the finger, but spread themselves in the manner of concentrical circles all round the finger, and are propagated on every side. For the gravity of the water supplies the place of elastic force.
Case 2. If the medium be not elastic, then, because its parts cannot be condensed by the pressure arising from the vibrating parts of the tremulous body, the motion will be propagated in an instant towards the parts where the medium yields most easily, that is, to the parts which the tremulous body would otherwise leave vacuous behind it. The case is the same with that of a body projected in any medium whatever. A medium yielding to projectiles does not recede in infinitum, but with a circular motion comes round to the spaces which the body leaves behind it. Therefore as often as a tremulous body tends to any part, the medium yielding to it comes round in a circle to the parts which the body leaves; and as often as the body returns to the first place, the medium will be driven from the place it came round to, and return to its original place. And though the tremulous body be not firm and hard, but every way flexible, yet if it continue of a given magnitude, since it cannot impel the medium by its tremors any where without yielding to it somewhere else, the medium receding from the parts of the body where it is pressed will always come round in a circle to the parts that yield to it. Q.E.D.
Cor. It is a mistake, therefore, to think, as some have done, that the agitation of the parts of flame conduces to the propagation of a pressure in rectilinear directions through an ambient medium. A pressure of that kind must be derived not from the agitation only of the parts of flame, but from the dilatation of the whole.
Proposition xliv. Theorem xxxv.
If water ascend and descend alternately in the erected legs KL, MN, of a canal or pipe; and a pendulum be constructed whose length between the point of suspension and the centre of oscillation is equal to half the length of the water in the canal; I say, that the water will ascend and descend in the same times in which the pendulum oscillates.
I measure the length of the water along the axes of the canal and its
legs, and make it equal to the sum of those axes; and take no notice
of the resistance of the water arising from its attrition by the sides
of the canal. Let, therefore, AB, CD, represent the mean height of the
water in both legs; and when the water in the leg KL ascends to the
height EF, the water will descend in the leg MN to the height GH. Let
P be a pendulous body, VP the thread, V the
point of suspension, RPQS the cycloid which
 the pendulum describes, P its lowest point, PQ an arc equal to the
height AE. The force with which the motion of the water is accelerated
and retarded alternately is the excess of the weight of the water in
one leg above the weight in the other; and, therefore, when the water
in the leg KL ascends to EF, and in the other leg descends to GH, that
force is double the weight of the water EABF, and therefore is to the
weight of the whole water as AE or PQ to VP or PR. The force also with
which the body P is accelerated or retarded in any place, as Q, of a
cycloid, is (by Cor. Prop. LI) to its whole weight as its distance PQ
from the lowest place P to the length PR of the cycloid. Therefore the
motive forces of the water and pendulum, describing the equal spaces
AE, PQ, are as the weights to be moved; and therefore if the water and
pendulum are quiescent at first, those forces will move them in equal
times, and will cause them to go and return together with a reciprocal
motion. Q.E.D.
the pendulum describes, P its lowest point, PQ an arc equal to the
height AE. The force with which the motion of the water is accelerated
and retarded alternately is the excess of the weight of the water in
one leg above the weight in the other; and, therefore, when the water
in the leg KL ascends to EF, and in the other leg descends to GH, that
force is double the weight of the water EABF, and therefore is to the
weight of the whole water as AE or PQ to VP or PR. The force also with
which the body P is accelerated or retarded in any place, as Q, of a
cycloid, is (by Cor. Prop. LI) to its whole weight as its distance PQ
from the lowest place P to the length PR of the cycloid. Therefore the
motive forces of the water and pendulum, describing the equal spaces
AE, PQ, are as the weights to be moved; and therefore if the water and
pendulum are quiescent at first, those forces will move them in equal
times, and will cause them to go and return together with a reciprocal
motion. Q.E.D.
Cor. 1. Therefore the reciprocations of the water in ascending and descending are all performed in equal times, whether the motion be more or less intense or remiss.
Cor. 2. If the length of the whole water in
the canal be of 6 1
9 feet of French measure, the
water will descend in one second of time, and will ascend in another
second, and so on by turns in infinitum; for a pendulum of 3
1
18 such feet in length will oscillate
in one second of time.
Cor. 3. But if the length of the water be increased or diminished, the time of the reciprocation will be increased or diminished in the subduplicate ratio of the length.
Proposition xlv. Theorem xxxvi.
The velocity of waves is in the subduplicate ratio of the breadths.
This follows from the construction of the following Proposition.
Proposition xlvi. Problem X.
To find the velocity of waves.
Let a pendulum be constructed, whose length between the point of suspension and the centre of oscillation is equal to the breadth of the waves and in the time that the pendulum will perform one single oscillation the waves will advance forward nearly a space equal to their breadth.
That which I call the breadth of the waves is the transverse measure
lying between the deepest part of the hollows,
 or the tops of the ridges. Let ABCDEF represent the surface of stagnant
water ascending and descending in successive waves; and let A, C, E,
&c., be the tops of the waves; and let B, D, F, &c., be the
intermediate hollows. Because the motion of the waves is carried on by
the successive ascent and descent of the water, so that the parts
thereof, as A, C, E, &c., which are highest at one time become
lowest immediately after; and because the motive force, by which the
highest parts descend and the lowest ascend, is the weight of the
elevated water, that alternate ascent and descent will be analogous to
the reciprocal motion of the water in the canal, and observe the same
laws as to the times of its ascent and descent; and therefore (by
Prop. XLIV) if the distances between the highest places of the waves
A, C, E, and the lowest B, D, F, be equal to twice the length of any
pendulum, the highest parts A, C, E, will become the lowest in the
time of one oscillation, and in the time of another oscillation will
ascend again. Therefore between the passage of each wave, the time of
two oscillations will intervene; that is, the wave will describe its
breadth in the time that pendulum will oscillate twice; but a pendulum
of four times that length, and which therefore is equal to the breadth
of the waves, will just oscillate once in that time.
Q.E.I.
or the tops of the ridges. Let ABCDEF represent the surface of stagnant
water ascending and descending in successive waves; and let A, C, E,
&c., be the tops of the waves; and let B, D, F, &c., be the
intermediate hollows. Because the motion of the waves is carried on by
the successive ascent and descent of the water, so that the parts
thereof, as A, C, E, &c., which are highest at one time become
lowest immediately after; and because the motive force, by which the
highest parts descend and the lowest ascend, is the weight of the
elevated water, that alternate ascent and descent will be analogous to
the reciprocal motion of the water in the canal, and observe the same
laws as to the times of its ascent and descent; and therefore (by
Prop. XLIV) if the distances between the highest places of the waves
A, C, E, and the lowest B, D, F, be equal to twice the length of any
pendulum, the highest parts A, C, E, will become the lowest in the
time of one oscillation, and in the time of another oscillation will
ascend again. Therefore between the passage of each wave, the time of
two oscillations will intervene; that is, the wave will describe its
breadth in the time that pendulum will oscillate twice; but a pendulum
of four times that length, and which therefore is equal to the breadth
of the waves, will just oscillate once in that time.
Q.E.I.
Cor. 1. Therefore waves, whose breadth is
equal to 3 1
18 French feet, will advance
through a space equal to their breadth in one second of time; and
therefore in one minute will go over a space of 183⅓ feet; and in an
hour a space of 11000 feet, nearly.
Cor. 2. And the velocity of greater or less waves will be augmented or diminished in the subduplicate ratio of their breadth.
These things are true upon the supposition that the parts of water ascend or descend in a right line; but, in truth, that ascent and descent is rather performed in a circle; and therefore I propose the time defined by this Proposition as only near the truth.
Proposition xlvii. Theorem xxxvii.
If pulses are propagated through a fluid, the several particles of the fluid, going and returning with the shortest reciprocal motion, are always accelerated or retarded according to the law of the oscillating pendulum.
Let AB, BC, CD, &c., represent equal distances of successive
pulses, ABC the line of direction of the motion of the successive
pulses propagated from A to B; E, F, G three
physical points of the quiescent medium situate in the right line AC
at equal distances from each other; Ee, Ff, Gg,
 equal spaces of extreme shortness,
through which those points go and return with a reciprocal motion in each
vibration; ε, Φ, γ, any intermediate places of the same
points; EF, FG physical lineolae, or linear parts of the medium lying
between those points, and successively transferred into the places εΦ,
Φγ, and ef, fg. Let there be drawn the right line PS
equal to the right line Ee. Bisect the same in O, and from
the centre O, with the interval OP, describe the circle SIPi.
Let the whole time of one vibration; with its proportional parts, be
expounded by the whole circumference of this circle and its parts, in
such sort, that, when any time PH or PHSh is completed, if
there be let fall to
equal spaces of extreme shortness,
through which those points go and return with a reciprocal motion in each
vibration; ε, Φ, γ, any intermediate places of the same
points; EF, FG physical lineolae, or linear parts of the medium lying
between those points, and successively transferred into the places εΦ,
Φγ, and ef, fg. Let there be drawn the right line PS
equal to the right line Ee. Bisect the same in O, and from
the centre O, with the interval OP, describe the circle SIPi.
Let the whole time of one vibration; with its proportional parts, be
expounded by the whole circumference of this circle and its parts, in
such sort, that, when any time PH or PHSh is completed, if
there be let fall to
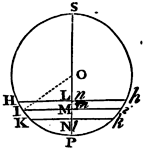 PS the perpendicular HL or hl,
and there be taken Eε equal to PL or Pl, the
physical point E may be found in ε. A point, as E, moving
according to this law with a reciprocal motion, in its going from E
through ε to e, and returning again through ε
to E, will perform its several vibrations with the same degrees of
acceleration and retardation with those of an oscillating pendulum. We
are now to prove that the several physical points of the medium will
be agitated with such a kind of motion. Let us suppose, then, that a
medium hath such a motion excited in it from any cause whatsoever, and
consider what will follow from thence.
PS the perpendicular HL or hl,
and there be taken Eε equal to PL or Pl, the
physical point E may be found in ε. A point, as E, moving
according to this law with a reciprocal motion, in its going from E
through ε to e, and returning again through ε
to E, will perform its several vibrations with the same degrees of
acceleration and retardation with those of an oscillating pendulum. We
are now to prove that the several physical points of the medium will
be agitated with such a kind of motion. Let us suppose, then, that a
medium hath such a motion excited in it from any cause whatsoever, and
consider what will follow from thence.
In the circumference PHSh let there be taken the equal arcs,
HI, IK, or hi, ik, having the same ratio to the whole
circumference as the equal right lines EF, FG have to BC, the whole
interval of the pulses. Let fall the perpendiculars IM, KN, or im,
kn; then because the points E, F, G are successively agitated
with like motions, and perform their entire vibrations composed of
their going and return, while the pulse is transferred from B to C; if
PH or PHSh be the time elapsed since the beginning of the
motion of the point E, then will PI or PHSi be the time
elapsed since the beginning of the motion of the point F, and PK or
PHSk the time elapsed since the beginning of the motion of
the point G; and therefore Eε, FΦ, Gγ, will
be respectively equal to PL, PM, PN, while the points are going, and
to Pl, Pm, Pn, when the points are
returning. Therefore εγ or EG + Gγ − Eε
will, when the points are going, be equal to EG − LN and
in their return equal to EG + ln. But εγ is the
breadth or expansion of the part EG of the medium in the place εγ;
and therefore the expansion of that part in its going is to its mean
expansion as EG − LN to EG; and in its return, as EG + ln or
EG + LN to EG. Therefore since LN is to KH as IM to the radius OP, and
KH to EG as the circumference PHShP to BC; that is, if we put
V for the radius of a circle whose circumference is equal to BC the
interval of the pulses, as OP to V; and, ex aequo, LN to EG
as IM to V; the expansion of the part EG, or of the physical point F
in the place εγ, to the mean expansion of the same part in
its first place EG, will be as V − IM to V in going, and as V + im
to V in its return. Hence the elastic force of the point P in the
place εγ to its mean elastic force in the place EG is as
1
V − IM to 1
V in its going, and
1
V + im to 1
V in its return. And by the same
reasoning the elastic forces of the physical points E and G in going
are as 1
V − HL and
1
V − KN to 1
V; and the difference of the forces
to the mean elastic force of the medium as HL
− KN
VV − V x HL − V x KN + HL x KN to
1
V; that is, as
HL − KN
VV to 1
V, or as HL − KN to V; if we suppose
(by reason of the very short extent of the vibrations) HL and KN to be
indefinitely less than the quantity V. Therefore since the quantity V
is given, the difference of the forces is as HL − KN; that is (because
HL − KN is proportional to HK, and OM to OI or OP; and because HK and
OP are given) as OM; that is, if Ff be bisected in Ω, as ΩΦ.
And for the same reason the difference of the elastic forces of the
physical points ε and γ, in the return of the
physical lineola εγ, is as ΩΦ. But that difference
(that is, the excess of the elastic force of the point ε
above the elastic force of the point γ) is the very force by which the
intervening physical lineola εγ of the medium is accelerated
in going, and retarded in returning; and therefore the accelerative
force of the physical lineola εγ is as its distance from Ω,
the middle place of the vibration. Therefore (by Prop. XXXVIII, Book
I) the time is rightly expounded by the arc PI; and the linear part of
the medium εγ is moved according to the law abovementioned,
that is, according to the law of a pendulum oscillating; and the case
is the same of all the linear parts of which the whole medium is
compounded. Q.E.D.
Cor. Hence it appears that the number of the pulses propagated is the same with the number of the vibrations of the tremulous body, and is not multiplied in their progress. For the physical lineola εγ as soon as it returns to its first place is at rest; neither will it move again, unless it receives a new motion either from the impulse of the tremulous body, or of the pulses propagated from that body. As soon, therefore, as the pulses cease to be propagated from the tremulous body, it will return to a state of rest, and move no more.
Proposition xlviii. Theorem xxxviii.
The velocities of pulses propagated in an elastic fluid are in a ratiο compounded of the subduplicate ratio of the elastic force directly, and the subduplicate ratio of the density inversely; supposing the elastic force of the fluid to be proportional to its condensation.
Case 1. If the mediums be homogeneous, and the distances of the pulses in those mediums be equal amongst themselves, but the motion in one medium is more intense than in the other, the contractions and dilatations of the correspondent parts will be as those motions; not that this proportion is perfectly accurate. However, if the contractions and dilatations are not exceedingly intense, the error will not be sensible; and therefore this proportion may be considered as physically exact. Now the motive elastic forces are as the contractions and dilatations; and the velocities generated in the same time in equal parts are as the forces. Therefore equal and corresponding parts of corresponding pulses will go and return together, through spaces proportional to their contractions and dilatations, with velocities that are as those spaces; and therefore the pulses, which in the time of one going and returning advance forward a space equal to their breadth, and are always succeeding into the places of the pulses that immediately go before them, will, by reason of the equality of the distances, go forward in both mediums with equal velocity.
Case 2. If the distances of the pulses or their lengths are greater in one medium than in another, let us suppose that the correspondent parts describe spaces, in going and returning, each time proportional to the breadths of the pulses; then will their contractions and dilatations be equal: and therefore if the mediums are homogeneous, the motive elastic forces, which agitate them with a reciprocal motion, will be equal also. Now the matter to be moved by these forces is as the breadth of the pulses; and the space through which they move every time they go and return is in the same ratio. And, moreover, the time of one going and returning is in a ratio compounded of the subduplicate ratio of the matter, and the subduplicate ratio of the space; and therefore is as the space. But the pulses advance a space equal to their breadths in the times of going once and returning once; that is, they go over spaces proportional to the times, and therefore are equally swift.
Case 3. And therefore in mediums of equal density and elastic force, all the pulses are equally swift. Now if the density or the elastic force of the medium were augmented, then, because the motive force is increased in the ratio of the elastic force, and the matter to be moved is increased in the ratio of the density, the time which is necessary for producing the same motion as before will be increased in the subduplicate ratio of the density, and will be diminished in the subduplicate ratio of the elastic force. And therefore the velocity of the pulses will be in a ratio compounded of the subduplicate ratio of the density of the medium inversely, and the subduplicate ratio of the elastic force directly. Q.E.D.
This Proposition will be made more clear from the construction of the following Problem.
Proposition xlix. Problem xi.
The density and elastic force of a medium being given, to find the velocity of the pulses.
Suppose the medium to be pressed by an incumbent weight after the manner of our air; and let A be the height of a homogeneous medium, whose weight is equal to the incumbent weight, and whose density is the same with the density of the compressed medium in which the pulses are propagated. Suppose a pendulum to be constructed whose length between the point of suspension and the centre of oscillation is A: and in the time in which that pendulum will perform one entire oscillation composed of its going and returning, the pulse will be propagated right onwards through a space equal to the circumference of a circle described with the radius A.
For, letting those things stand which were constructed in Prop.
XLVII, if any physical line, as EF, describing the space PS in each
vibration, be acted on in the extremities P and S of every going and
return that it makes by an elastic force that is equal to its weight,
it will perform its several vibrations in the time in which the same
might oscillate in a cycloid whose whole perimeter is equal to the
length PS; and that because equal forces will impel equal corpuscles
through equal spaces in the same or equal times. Therefore since the
times of the oscillations are in the subduplicate ratio of the lengths
of the pendulums, and the length of the pendulum is equal to half the
arc of the whole cycloid, the time of one vibration would be to the
time of the oscillation of a pendulum whose length is A in the
subduplicate ratio of the length ½PS or PO to the length A. But the
elastic force with which the physical lineola EG is urged, when it is
found in its extreme places P, S, was (in the demonstration of Prop.
XLVII) to its whole elastic force as HL − KN to V, that is (since the
point K now falls upon P), as HK to V: and all that force, or which is
the same thing, the incumbent weight by which the lineola EG is
compressed, is to the weight of the lineola as the altitude A of the
incumbent weight to EG the length of the lineola; and therefore, ex
aequo, the force
 with which the lineola EG is urged in the places P and S is to the
weight of that lineola as HK x A to V x EG; or as PO x A to VV;
because HK was to EG as PO to V. Therefore since the times in which
equal bodies are impelled through equal spaces are reciprocally in the
subduplicate ratio of the forces, the time of one vibration, produced
by the action of that elastic force, will be to the time of a
vibration, produced by the impulse of the weight in a subduplicate
ratio of VV to PO x A, and therefore to the time of the oscillation of
a pendulum whose length is A in the subduplicate ratio of VV to PO x
A, and the subduplicate ratio of PO to A conjunctly; that is, in the
entire ratio of V to A.
with which the lineola EG is urged in the places P and S is to the
weight of that lineola as HK x A to V x EG; or as PO x A to VV;
because HK was to EG as PO to V. Therefore since the times in which
equal bodies are impelled through equal spaces are reciprocally in the
subduplicate ratio of the forces, the time of one vibration, produced
by the action of that elastic force, will be to the time of a
vibration, produced by the impulse of the weight in a subduplicate
ratio of VV to PO x A, and therefore to the time of the oscillation of
a pendulum whose length is A in the subduplicate ratio of VV to PO x
A, and the subduplicate ratio of PO to A conjunctly; that is, in the
entire ratio of V to A.
 But in the time of one vibration composed of the going and returning of the pendulum,
the pulse will be propagated right onward through a space equal to its breadth BC.
Therefore the time in which a pulse runs over the space BC is to the
time of one oscillation composed of the going and returning of the
pendulum as V to A, that is, as BC to the circumference of a circle
whose radius is A. But the time in which the pulse will run over the
space BC is to the time in which it will run over a length equal to
that circumference in the same ratio; and therefore in the time of
such an oscillation the pulse will run over a length equal to that
circumference. Q.E.D.
But in the time of one vibration composed of the going and returning of the pendulum,
the pulse will be propagated right onward through a space equal to its breadth BC.
Therefore the time in which a pulse runs over the space BC is to the
time of one oscillation composed of the going and returning of the
pendulum as V to A, that is, as BC to the circumference of a circle
whose radius is A. But the time in which the pulse will run over the
space BC is to the time in which it will run over a length equal to
that circumference in the same ratio; and therefore in the time of
such an oscillation the pulse will run over a length equal to that
circumference. Q.E.D.
Cor. 1. The velocity of the pulses is equal to that which heavy bodies acquire by falling with an equally accelerated motion, and in their fall describing half the altitude A. For the pulse will, in the time of this fall, supposing it to move with the velocity acquired by that fall, run over a space that will be equal to the whole altitude A; and therefore in the time of one oscillation composed of one going and return, will go over a space equal to the circumference of a circle described with the radius A; for the time of the fall is to the time of oscillation as the radius of a circle to its circumference.
Cor. 2. Therefore since that altitude A is as the elastic force of the fluid directly, and the density of the same inversely, the velocity of the pulses will be in a ratio compounded of the subduplicate ratio of the density inversely, and the subduplicate ratio of the elastic force directly.
Proposition l. Problem xii.
To find the distances of the pulses.
Let the number of the vibrations of the body, by whose tremor the pulses are produced, be found to any given time. By that number divide the space which a pulse can go over in the same time, and the part found will be the breadth of one pulse. Q.E.I.
Scholium.
The last Propositions respect the motions of light and sounds; for
since light is propagated in right lines, it is certain that it cannot
consist in action alone (by Prop. XLI and XLII). As to sounds, since
they arise from tremulous bodies, they can be nothing else but pulses
of the air propagated through it (by Prop. XLIII); and this is
confirmed by the tremors which sounds, if they be loud and deep,
excite in the bodies near them, as we experience in the sound of
drums; for quick and short tremors are less easily excited. But it is
well known that any sounds, falling upon strings in unison with the
sonorous bodies, excite tremors in those strings. This is also
confirmed from the velocity of sounds; for since the specific
gravities of rain-water and quicksilver are to one another as about 1
to 13⅔, and when the mercury in the barometer is at the height of 30
inches of our measure, the specific gravities of the air and of
rain-water are to one another as about 1 to 870, therefore the
specific gravity of air and quicksilver are to each other as 1 to
11890. Therefore when the height of the quicksilver is at 30 inches, a
height of uniform air, whose weight would be sufficient to compress
our air to the density we find it to be of, must be equal to 356700
inches, or 29725 feet of our measure; and this is that very height of
the medium, which I have called A in the construction of the foregoing
Proposition. A circle whose radius is 29725 feet is 186768 feet in
circumference. And since a pendulum 39 1
5 inches in length completes one
oscillation, composed of its going and return, in two seconds of time,
as is commonly known, it follows that a pendulum 29725 feet, or 356700
inches in length will perform a like oscillation in 190¾ seconds.
Therefore in that time a sound will go right onwards 186768 feet, and
therefore in one second 979 feet.
But in this computation we have made no allowance for the crassitude
of the solid particles of the air, by which the sound is propagated
instantaneously. Because the weight of air is to the weight of water
as 1 to 870, and because salts are almost twice as dense as water; if
the particles of air are supposed to be of near the same density as
those of water or salt, and the rarity of the air arises from the
intervals of the particles; the diameter of one particle of air will
be to the interval between the centres of the
particles as 1 to about 9 or 10, and to the interval between the
particles themselves as 1 to 8 or 9. Therefore to 979 feet, which,
according to the above calculation, a sound will advance forward in
one second of time, we may add 979
9, or about 109 feet, to compensate for
the crassitude of the particles of the air: and then a sound will go
forward about 1088 feet in one second of time.
Moreover, the vapours floating in the air being of another spring, and a different tone, will hardly, if at all, partake of the motion of the true air in which the sounds are propagated. Now if these vapours remain unmoved, that motion will be propagated the swifter through the true air alone, and that in the subduplicate ratio of the defect of the matter. So if the atmosphere consist of ten parts of true air and one part of vapours, the motion of sounds will be swifter in the subduplicate ratio of 11 to 10, or very nearly in the entire ratio of 21 to 20, than if it were propagated through eleven parts of true air: and therefore the motion of sounds above discovered must be increased in that ratio. By this means the sound will pass through 1142 feet in one second of time.
These things will be found true in spring and autumn, when the air is rarefied by the gentle warmth of those seasons, and by that means its elastic force becomes somewhat more intense. But in winter, when the air is condensed by the cold, and its elastic force is somewhat remitted, the motion of sounds will be slower in a subduplicate ratio of the density; and, on the other hand, swifter in the summer.
Now by experiments it actually appears that sounds do really advance in one second of time about 1142 feet of English measure, or 1070 feet of French measure.
The velocity of sounds being known, the intervals of the pulses are
known also. For M. Sauveur, by some experiments that he
made, found that an open pipe about five Paris feet in
length gives a sound of the same tone with a viol-string that vibrates
a hundred times in one second. Therefore there are near 100 pulses in
a space of 1070 Paris feet, which a sound runs over in a
second of time; and therefore one pulse fills up a space of about 10
7
10 Paris feet, that is, about
twice the length of the pipe. From whence it is probable that the
breadths of the pulses, in all sounds made in open pipes, are equal to
twice the length of the pipes.
Moreover, from the Corollary of Prop. XLVII appears the reason why the sounds immediately cease with the motion of the sonorous body, and why they are heard no longer when we are at a great distance from the sonorous bodies than when we are very near them. And besides, from the foregoing principles, it plainly appears how it comes to pass that sounds are so mightily increased in speaking-trumpets; for all reciprocal motion uses to be increased by the generating cause at each return. And in tubes hindering the dilatation of the sounds, the motion decays more slowly, and recurs more forcibly; and therefore is the more increased by the new motion impressed at each return. And these are the principal phaenomena of sounds.