Section V.
How the orbits are to be found when neither focus is given.
Lemma xvii.
If from any point P of a given conic section, to the four produced sides AB, CD, AC, DB, of any trapezium ABDC inscribed in that section, as many right lines PQ, PR, PS, PT are drawn in given angles, each line to each side; the rectangle PQ x PR of those on the opposite sides AB, CD, will be to the rectangle PS x PT of those on the other two opposite sides AC, BD, in a given ratio.
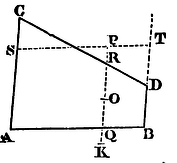
Case 1. Let us suppose, first, that the lines drawn to one pair of opposite sides are parallel to either of the other sides; as PQ and PR to the side AC, and PS and PT to the side AB. And farther, that one pair of the opposite sides, as AC and BD, are parallel betwixt themselves; then the right line which bisects those parallel sides will be one of the diameters of the conic section, and will likewise bisect RQ. Let O be the point in which RQ is bisected, and PO will be an ordinate to that diameter. Produce PO to K, so that OK may be equal to PO, and OK will be an ordinate on the other side of that diameter. Since, therefore, the points A, B, P and K are placed in the conic section, and PK cuts AB in a given angle, the rectangle PQK (by Prop. XVII., XIX., XXI. and XXIII., Book III., of Apollonius's Conics) will be to the rectangle AQB in a given ratio. But QK and PR are equal, as being the differences of the equal lines OK, OP, and OQ, OR; whence the rectangles PQK and PQ x PR are equal; and therefore the rectangle PQ x PR is to the rectangle A B, that is, to the rectangle PS x PT in a given ratio. Q.E.D
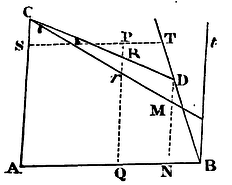
Case 2. Let us next suppose that the opposite sides AC and BD of the trapezium are not parallel. Draw Bd parallel to AC, and meeting as well the right line ST in t, as the conic section in d. Join Cd cutting PQ in r, and draw DM parallel to PQ, cutting Cd in M, and AB in N. Then (because of the similar triangles BTt, DBN), Bt or PQ is to Tt as DN to NB. And so Rr is to AQ or PS as DM to AN. Wherefore, by multiplying the antecedents by the antecedents, and the consequents by the consequents, as the rectangle PQ x Rr is to the rectangle PS x Tt, so will the rectangle NDM be to the rectangle ANB; and (by Case 1) so is the rectangle PQ x Pr to the rectangle PS x Pt; and by division, so is the rectangle PQ x PR to the rectangle PS x PT. Q.E.D.
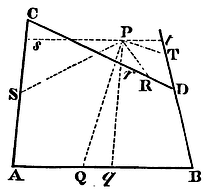
Case 3. Let us suppose, lastly, the four lines PQ, PR, PS, PT, not to be parallel to the sides AC, AB, but any way inclined to them. In their place draw Pq, Pr, parallel to AC; and Ps, Pt parallel to AB; and because the angles of the triangles PQq, PRr, PSs, PTt are given, the ratios of PQ to Pq, PR to Pr, PS to Ps, PT to Pt will be also given; and therefore the compounded ratios PQ x PR to Pq x Pr, and PS x PT to Ps x Pt are given. But from what we have demonstrated before, the ratio of Pq x Pr to Ps x Pt is given; and therefore also the ratio of PQ x PR to PS x PT. Q.E.D.
Lemma xviii.
The same things supposed, if the rectangle PQ x PR of the lines drawn to the two opposite sides of the trapezium is to the rectangle PS x PT of those drawn to the other two sides in a given ratio, the point P, from whence those lines are drawn, will be placed in a conic section described about the trapezium.
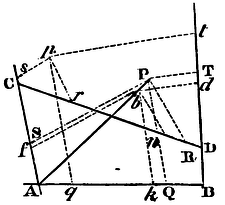
Conceive a conic section to be described passing through the points A, B, C, D, and any one of the infinite number of points P, as for example p; I say, the point P will be always placed in this section. If you deny the thing, join AP cutting this conic section somewhere else, if possible, than in P, as in b. Therefore if from those points p and b, in the given angles to the sides of the trapezium, we draw the right lines pq, pr, ps, pt, and bk, bn, bf, bd, we shall have, as bk x bn to bf x bd, so (by Lem. XVII) pq x pr to ps x pt; and so (by supposition) PQ x PR to PS x PT. And because of the similar trapezia bkAf, PQAS, as bk to bf, so PQ to PS. Wherefore by dividing the terms of the preceding proportion by the correspondent terms of this, we shall have bn to bd as PR to PT. And therefore the equiangular trapezia Dnbd, DRPT, are similar, and consequently their diagonals Db, DP do coincide. Wherefore b falls in the intersection of the right lines AP, DP, and consequently coincides with the point P. And therefore the point P, wherever it is taken, falls to be in the assigned conic section. Q.E.D.
Cor. Hence if three right lines PQ, PR, PS, are drawn from a common point P, to as many other right lines given in position, AB, CD, AC, each to each, in as many angles respectively given, and the rectangle PQ x PR under any two of the lines drawn be to the square of the third PS in a given ratio; the point P, from which the right lines are drawn, will be placed in a conic section that touches the lines AB, CD in A and C; and the contrary. For the position of the three right lines AB, CD, AC remaining the same, let the line BD approach to and coincide with the line AC; then let the line PT come likewise to coincide with the line PS; and the rectangle PS x PT will become PS², and the right lines AB, CD, which before did cut the curve in the points A and B, C and D, can no longer cut, but only touch, the curve in those coinciding points.
Scholium.

In this Lemma, the name of conic section is to be understood in a large sense, comprehending as well the rectilinear section through the vertex of the cone, as the circular one parallel to the base. For if the point p happens to be in a right line, by which the points A and D, or C and B are joined, the conic section will be changed into two right lines, one of which is that right line upon which the point p falls, and the other is a right line that joins the other two of the four points. If the two opposite angles of the trapezium taken together are equal to two right angles, and if the four lines PQ, PR, PS, PT, are drawn to the sides thereof at right angles, or any other equal angles, and the rectangle PQ x PR under two of the lines drawn PQ and PR, is equal to the rectangle PS x PT under the other two PS and PT, the conic section will become a circle. And the same thing will happen if the four lines are drawn in any angles, and the rectangle PQ x PR, under one pair of the lines drawn, is to the rectangle PS x PT under the other pair as the rectangle under the sines of the angles S, T, in which the two last lines PS, PT are drawn to the rectangle under the sines of the angles Q, R, in which the first two PQ, PR are drawn. In all other cases the locus of the point P will be one of the three figures which pass commonly by the name of the conic sections. But in room of the trapezium ABCD, we may substitute a quadrilateral figure whose two opposite sides cross one another like diagonals. And one or two of the four points A, B, C, D may be supposed to be removed to an infinite distance, by which means the sides of the figure which converge to those points, will become parallel; and in this case the conic section will pass through the other points, and will go the same way as the parallels in infinitum.
Lemma xix.
To find a point P from which if four right lines PQ, PR, PS, PT are drawn to as many other right lines AB, CD, AC, BD, given by position, each to each, at given angles, the rectangle PQ x PR, under any two of the lines drawn, shall be to the rectangle PS x PT, under the other two, in a given ratio.
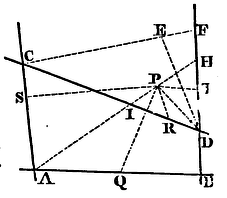
Suppose the lines AB, CD, to which the two right lines PQ, PR, containing one of the rectangles, are drawn to meet two other lines, given by position, in the points A, B, C, D. From one of those, as A, draw any right line AH, in which you would find the point P. Let this cut the opposite lines BD, CD, in H and I; and, because all the angles of the figure are given, the ratio of PQ to PA, and PA to PS, and therefore of PQ to PS, will be also given. Subducting this ratio from the given ratio of PQ x PR to PS x PT, the ratio of PR to PT will be given; and adding the given ratios of PI to PR, and PT to PH, the ratio of PI to PH, and therefore the point P will be given. Q.E.I.
Cor. 1. Hence also a tangent may be drawn to any point D of the locus of all the points P. For the chord PD, where the points P and D meet, that is, where AH is drawn through the point D, becomes a tangent. In which case the ultimate ratio of the evanescent lines IP and PH will be found as above. Therefore draw CF parallel to AD, meeting BD in F, and cut it in E in the same ultimate ratio, then DE will be the tangent; because CF and the evanescent IH are parallel, and similarly cut in E and P.
Cor. 2. Hence also the locus of all the
points P may be determined. Through any of the points A, B, C, D, as
A, draw AE touching the locus, and through any other point B parallel
to the tangent, draw BF meeting the locus in F; and find the point F
by this Lemma. Bisect BF in G, and, drawing the indefinite line AG,
this will be the position of the diameter to which BG and FG are
ordinates. Let this AG meet the locus
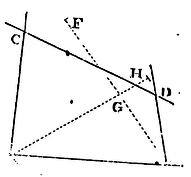 in H, and AH will be its diameter or latus transversum, to which the
latus rectum will be as BG² to AG x GH. If AG nowhere meets the locus,
the line AH being infinite, the locus will be a parabola; and its
latus rectum corresponding to the diameter AG will be
BG2
in H, and AH will be its diameter or latus transversum, to which the
latus rectum will be as BG² to AG x GH. If AG nowhere meets the locus,
the line AH being infinite, the locus will be a parabola; and its
latus rectum corresponding to the diameter AG will be
BG2
AG. But if it does meet it anywhere,
the locus will be an hyperbola, when the points A and H are placed on
the same side the point G; and an ellipsis, if the point G falls
between the points A and H; unless, perhaps, the angle AGB is a right
angle, and at the same time BG² equal to the rectangle AGH, in which
case the locus will be a circle.
And so we have given in this Corollary a solution of that famous Problem of the ancients concerning four lines, begun by Euclid, and carried on by Apollonius; and this not an analytical calculus, but a geometrical composition, such as the ancients required.
Lemma xx.
If the two opposite angular points A and P of any parallelogram ASPQ touch any conic section in the points A and P; and the sides AQ, AS of one of those angles, indefinitely produced, meet the same conic section in B and C; and from the points of concourse B and C to any fifth point D of the conic section, two right lines BD, CD are drawn meeting the two other sides PS, PQ of the parallelogram, indefinitely produced in T and R; the parts PR and PT, cut off from the sides, will always be one to the other in a given ratio. And vice versa, if those parts cut off are one to the other in a given ratio, the locus of the point D will be a conic section passing through the four points A, B, C, P.
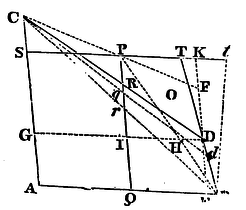
Case 1. Join BP, CP, and from the point D draw the two right lines DG, DE, of which the first DG shall be parallel to AB, and meet PB, PQ, CA in H, I, G; and the other DE shall be parallel to AC, and meet PC, PS, AB, in F, K, E; and (by Lem. XVII) the rectangle DE x DF will be to the rectangle DG x DH in a given ratio. But PQ is to DE (or IQ) as PB to HB, and consequently as PT to DH; and by permutation PQ is to PT as DE to DH. Likewise PR is to DF as RC to DC, and therefore as (IG or) PS to DG; and by permutation PR is to PS as DF to DG; and, by compounding those ratios, the rectangle PQ x PR will be to the rectangle PS x PT as the rectangle DE x DF is to the rectangle DG x DH, and consequently in a given ratio. But PQ and PS are given, and therefore the ratio of PR to PT is given. Q.E.D.
Case 2. But if PR and PT are supposed to be in a given ratio one to the other, then by going back again, by a like reasoning, it will follow that the rectangle DE x DF is to the rectangle DG x DH in a given ratio; and so the point D (by Lem. XVIII) will lie in a conic section passing through the points A, B, C, P, as its locus. Q.E.D.
Cor. 1. Hence if we draw BC cutting PQ in r and in PT take Pt to Pr in the same ratio which PT has to PR; then Bt will touch the conic section in the point B. For suppose the point D to coalesce with the point B, so that the chord BD vanishing, BT shall become a tangent, and CD and BT will coincide with CB and Bt.
Cor. 2. And, vice versa, if Bt is a tangent, and the lines BD, CD meet in any point D of a conic section, PR will be to PT as Pr to Pt. And, on the contrary, if PR is to PT as Pr to Pt, then BD and CD will meet in some point D of a conic section.
Cor. 3. One conic section cannot cut another conic section in more than four points. For, if it is possible, let two conic sections pass through the five points A, B, C, P, O; and let the right line BD cut them in the points D, d, and the right line Cd cut the right line PQ in q. Therefore PR is to PT as Pq to PT: whence PR and Pq are equal one to the other, against the supposition.
Lemma xxi.
If two moveable and indefinite right lines BM, CM drawn through given points B, C, as poles, do by their point of concourse M describe a third right line MN given by position; and other two indefinite right lines BD, CD are drawn, making with the former two at those given points B, C, given angles, MBD, MCD: I say, that those two right lines BD, CD will by their point of concourse D describe a conic section passing through the points B, C. And, vice versa, if the right lines BD, CD do by their point of concourse D describe a conic section passing through the given points B, C, A, and the angle DBM Is always equal to the given angle ABC, as well as the angle DCM always equal to the given angle ACB, the point M will lie in a right line given by position,as its locus.
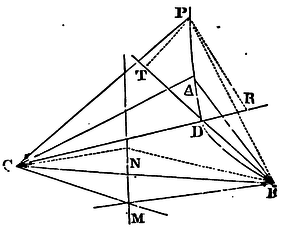
For in the right line MN let a point N be given, and when the moveable point M falls on the immoveable point N. let the moveable point D fall on an immovable point P. Join CN, BN, CP, BP, and from the point P draw the right lines PT, PR meeting BD, CD in T and R, and making the angle BPT equal to the given angle BNM, and the angle CPR equal to the given angle CNM. Wherefore since (by supposition) the angles MBD, NBP are equal, as also the angles MCD, NCP, take away the angles NBD and NCD that are common, and there will remain the angles NBM and PBT, NCM and PCR equal; and therefore the triangles NBM, PBT are similar, as also the triangles NCM, PCR. Wherefore PT is to NM as PB to NB; and PR to NM as PC to NC. But the points, B, C, N, P are immovable: wherefore PT and PR have a given ratio to NM, and consequently a given ratio between themselves; and therefore, (by Lemma XX) the point D wherein the moveable right lines BT and CR perpetually concur, will be placed in a conic section passing through the points B, C, P. Q.E.D.
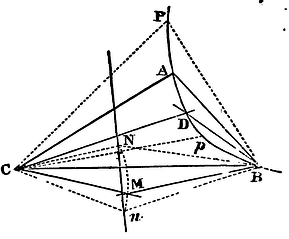
And, vice versa, if the moveable point D lies in a conic section passing through the given points B, C, A; and the angle DBM is always equal to the given angle ABC, and the angle DCM always equal to the given angle ACB, and when the point D falls successively on any two immovable points p, P, of the conic section, the moveable point M falls successively on two immovable points n, N. Through these points n, N, draw the right line nN: this line nN will be the perpetual locus of that moveable point M. For, if possible, let the point M be placed in any curve line. Therefore the point D will be placed in a conic section passing through the five points B, C, A, p, P, when the point M is perpetually placed in a curve line. But from what was demonstrated before, the point D will be also placed in a conic section passing through the same five points B, C, A, p, when the point M is perpetually placed in a right line. Wherefore the two conic sections will both pass through the same five points, against Corol. 3, Lem. XX. It is therefore absurd to suppose that the point M is placed in a curve line. Q.E.D.
Proposition xxii. Problem xiv.
To describe a trajectory that shall pass through five given points.
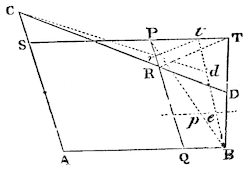
Let the five given points be A, B, C, P, D. From any one of them, as A, to any other two as B, C, which may be called the poles, draw the right lines AB, AC, and parallel to those the lines TPS, PRQ, through the fourth point P. Then from the two poles B, C, draw through the fifth point D two indefinite lines BDT, CRD, meeting with the last drawn lines TPS, PRQ (the former with the former, and the latter with the latter) in T and R. Then drawing the right line tr parallel to TR, cutting off from the right lines PT, PR, any segments Pt, Pr, proportional to PT, PR; and if through their extremities, t, r, and the poles B, C, the right lines Bt, Cr are drawn, meeting in d, that point d will be placed in the trajectory required. For (by Lem. XX) that point d is placed in a conic section passing through the four points A, B, C, P; and the lines Rr, Tt vanishing, the point d comes to coincide with the point D. Wherefore the conic section passes through the five points A, B, C, P, D. Q.E.D.
The same otherwise.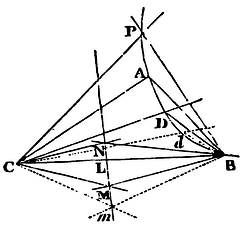
Of the given points join any three, as A, B, C; and about two of them B, C, as poles, making the angles ABC, ACB of a given magnitude to revolve, apply the legs BA, CA, first to the point D, then to the point P, and mark the points M, N, in which the other legs BL, CL intersect each other in both cases. Draw the indefinite right line MN, and let those moveable angles revolve about their poles B, C, in such manner that the intersection, which is now supposed to be d, of the legs BL, CL, or BM, CM, may always fall in that indefinite right line MN; and the intersection, which is now supposed to be m, of the legs BA, CA, or BD, CD, will describe the trajectory required, PADdB. For (by Lem. XXI) the point d will be placed in a conic section passing through the points B, C; and when the point m comes to coincide with the points L, M, N, the point d will (by construction) come to coincide with the points A, D, P. Wherefore a conic section will be described that shall pass through the five points A, B. C, P, D. Q.E.F.
Cor. 1. Hence a right line may be readily drawn which shall be a tangent to the trajectory in any given point B. Let the point d come to coincide with the point B, and the right line Bd will become the tangent required.
Cor. 2. Hence also may be found the centres, diameters, and latera recta of the trajectories, as in Cor. 2, Lem. XIX.
Scholium.
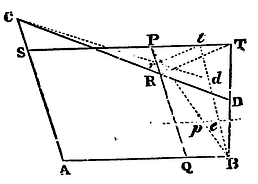
The former of these constructions will become something more simple by joining BP, and in that line, produced, if need be, taking Bp to BP as PR is to PT; and through p draw the indefinite right line pe parallel to SPT, and in that line pe taking always pe equal to Pr, and draw the right lines Be, Cr to meet in d. For since Pr to Pt, PR to PT, pB to PB, pe to Pt, are all in the same ratio, pe and Pr will be always equal. After this manner the points of the trajectory are most readily found, unless you would rather describe the curve mechanically, as in the second construction.
Proposition xxiii. Problem xv.
To describe a trajectory that shall pass through four given points, and touch a right line given by position.
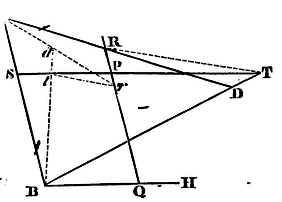
Case 1. Suppose that HB is the given tangent, B the point of contact, and C, D, P, the three other given points. Join BC, and draw PS parallel to BH, and PQ parallel to BC; complete the parallelogram BSPQ. Draw BD cutting SP in T, and CD cutting PQ in R. Lastly, draw any line tr parallel to TR, cutting off from PQ, PS, the segments Pr, Pt proportional to PR, PT respectively; and draw Cr, Bt their point of concourse d will (by Lem. XX) always fall on the trajectory to be described.
The same otherwise.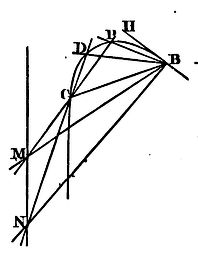
Let the angle CBH of a given magnitude revolve about the pole B; as also the rectilinear radius BC, both ways produced, about the pole C. Mark the points M, N, on which the leg BC of the angle cuts that radius when BH, the other leg thereof, meets the same radius in the points P and D. Then drawing the indefinite line MN, let that radius CP or CD and the leg BC of the angle perpetually meet in this line; and the point of concourse of the other leg BH with the radius will delineate the trajectory required.
For if in the constructions of the preceding Problem the point A comes to a coincidence with the point B, the lines CA and CB will coincide, and the line AB, in its last situation, will become the tangent BH; and therefore the constructions there set down will become the same with the constructions here described. Wherefore the concourse of the leg BH with the radius will describe a conic section passing through the points C, D, P, and touching the line BH in the point B. Q.E.F.
Case 2. Suppose the four points B, C, D, P,
given, being situated with out the tangent HI. Join each two by the
lines BD, CP meeting in G, and cutting the tangent in H and I. Cut the
tangent in A in such manner
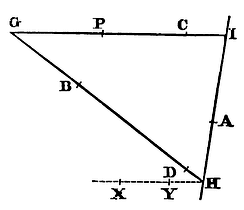 that HA may be to IA as the rectangle under a mean proportional
between CG and GP, and a mean proportional between BH and HD is to a
rectangle under a mean proportional between GD and GB, and a mean
proportional between PI and IC, and A will be the point of contact.
For if HX, a parallel to the right line PI, cuts the trajectory in any
points X and Y, the point A (by the properties of the conic sections)
will come to be so placed, that HA² will become to AI² in a ratio that
is compounded out of the ratio of the rectangle XHY to the rectangle
BHD, or of the rectangle CGP to the rectangle DGB; and the ratio of
the rectangle BHD to the rectangle PIC. But after the point of contact
A is found, the trajectory will be described as in the first Case.
Q.E.F. But the point A may be taken either
between or without the points H and I, upon which account a twofold
trajectory may be described.
that HA may be to IA as the rectangle under a mean proportional
between CG and GP, and a mean proportional between BH and HD is to a
rectangle under a mean proportional between GD and GB, and a mean
proportional between PI and IC, and A will be the point of contact.
For if HX, a parallel to the right line PI, cuts the trajectory in any
points X and Y, the point A (by the properties of the conic sections)
will come to be so placed, that HA² will become to AI² in a ratio that
is compounded out of the ratio of the rectangle XHY to the rectangle
BHD, or of the rectangle CGP to the rectangle DGB; and the ratio of
the rectangle BHD to the rectangle PIC. But after the point of contact
A is found, the trajectory will be described as in the first Case.
Q.E.F. But the point A may be taken either
between or without the points H and I, upon which account a twofold
trajectory may be described.
Proposition xxiv. Problem xvi.
To describe a trajectory that shall pass through three given points, and touch two right lines given by position.
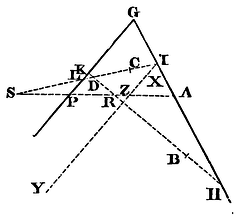
Suppose HI, KL to be the given tangents and B, C, D, the given points. Through any two of those points, as B, D, draw the indefinite right line BD meeting the tangents in the points H, K. Then likewise through any other two of these points, as C, D, draw the indefinite right line CD meeting the tangents in the points I, L. Cut the lines drawn in R and S, so that HR may be to KR as the mean proportional between BH and HD is to the mean proportional between BK and KD; and IS to LS as the mean proportional between CI and ID is to the mean proportional between CL and LD. But you may cut, at pleasure, either within or between the points K and H, I and L, or without them; then draw RS cutting the tangents in A and P, and A and P will be the points of contact. For if A and P are supposed to be the points of contact, situated anywhere else in the tangents, and through any of the points H, I, K, L, as I, situated in either tangent HI, a right line IY is drawn parallel to the other tangent KL, and meeting the curve in X and Y, and in that right line there be taken IZ equal to a mean proportional between IX and IY, the rectangle XIY or IZ², will (by the properties of the conic sections) be to LP² as the rectangle CID is to the rectangle CLD, that is (by the construction), as SI is to SL², and therefore IZ is to LP as SI to SL. Wherefore the points S, P, Z, are in one right line. Moreover, since the tangents meet in G, the rectangle XIY or IZ² will (by the properties of the conic sections) be to IA² as GP² is to GA², and consequently IZ will be to IA as GP to GA. Wherefore the points P, Z, A, lie in one right line, and therefore the points S, P, and A are in one right line. And the same argument will prove that the points R, P, and A are in one right line. Wherefore the points of contact A and P lie in the right line RS. But after these points are found, the trajectory may be described, as in the first Case of the preceding Problem. Q.E.F.
In this Proposition, and Case 2 of the foregoing, the constructions are the same, whether the right line XY cut the trajectory in X and Y, or not; neither do they depend upon that section. But the constructions being demonstrated where that right line does cut the trajectory, the constructions where it does not are also known; and therefore, for brevity's sake, I omit any farther demonstration of them.
Lemma xxii.
To transform figures into other figures of the same kind.
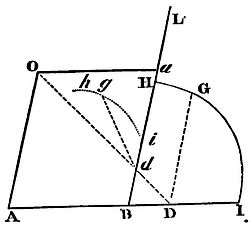
Suppose that any figure HGI is to be transformed. Draw, at pleasure, two parallel lines AO, BL, cutting any third line AB, given by position, in A and B, and from any point G of the figure, draw out any right line GD, parallel to OA, till it meet the right line AB. Then from any given point O in the line OA, draw to the point D the right line OD, meeting BL in d; and from the point of concourse raise the right line dg containing any given angle with the right line BL, and having such ratio to Od as DG has to OD; and g will be the point in the new figure hgi, corresponding to the point G. And in like manner the several points of the first figure will give as many correspondent points of the new figure. If we therefore conceive the point G to be carried along by a continual motion through all the points of the first figure, the point g will be likewise carried along by a continual motion through all the points of the new figure, and describe the same. For distraction's sake, let us call DG the first ordinate, dg the new ordinate, AD the first abscissa, ad the new abscissa; O the pole, OD the abscinding radius, OA the first ordinate radius, and Oa (by which the parallelogram OABa is completed) the new ordinate radius.
I say, then, that if the point G is placed in a right line given by
position, the point g will be also placed in a right line
given by position. If the point G is placed in a conic section, the
point g will be likewise placed in
a conic section. And here I understand the circle as one of the conic
sections. But farther, if the point G is placed in a line of the third
analytical order, the point g will also be placed in a line
of the third order, and so on in curve lines of higher orders. The two
lines in which the points G, g, are placed, will be always
of the same analytical order. For as ad is to OA, so are Od
to OD, dg to DG, and AB to AD; and therefore AD is equal to
OA x AB
ad, and DG equal to
OA x dg
ad. Now if the point G is placed in a
right line, and therefore, in any equation by which the relation
between the abscissa AD and the ordinate GD is expressed, those
indetermined lines AD and DG rise no higher than to one dimension, by
writing this equation OA x AB
ad in place of AD, and
OA x dg
ad in place of DG, a new equation will
be produced, in which the new abscissa ad and new ordinate dg
rise only to one dimension; and which therefore must denote a right
line. But if AD and DG (or either of them) had risen to two dimensions
in the first equation, ad and dg would likewise
have risen to two dimensions in the second equation. And so on in
three or more dimensions. The indetermined lines, ad, dg in
the second equation, and AD, DG, in the first, will always rise to the
same number of dimensions; and therefore the lines in which the points
G, g, are placed are of the same analytical order.
I say farther, that if any right line touches the curve line in the first figure, the same right line transferred the same way with the curve into the new figure will touch that curve line in the new figure, and vice versa. For if any two points of the curve in the first figure are supposed to approach one the other till they come to coincide, the same points transferred will approach one the other till they come to coincide in the new figure; and therefore the right lines with which those points are joined will be come together tangents of the curves in both figures. I might have given demonstrations of these assertions in a more geometrical form; but I study to be brief.
Wherefore if one rectilinear figure is to be transformed into another, we need only transfer the intersections of the right lines of which the first figure consists, and through the transferred intersections to draw right lines in the new figure. But if a curvilinear figure is to be transformed, we must transfer the points, the tangents, and other right lines, by means of which the curve line is defined. This Lemma is of use in the solution of the more difficult Problems; for thereby we may transform the proposed figures, if they are intricate, into others that are more simple. Thus any right lines converging to a point are transformed into parallels, by taking for the first ordinate radius any right line that passes through the point of concourse of the converging lines, and that because their point of concourse is by this means made to go off in infinitum; and parallel lines are such as tend to a point infinitely remote. And after the problem is solved in the new figure, if by the inverse operations we transform the new into the first figure, we shall have the solution required.
This Lemma is also of use in the solution of solid problems. For as often as two conic sections occur, by the intersection of which a problem may be solved, any one of them may be transformed, if it is an hyperbola or a parabola, into an ellipsis, and then this ellipsis may be easily changed into a circle. So also a right line and a conic section, in the construction of plane problems, may be transformed into a right line and a circle
Proposition xxv. Problem xvii.
To describe a trajectory that shall pass through two given points, and touch three right lines given by position.
Through the concourse of any two of the tangents one with the other,
and the concourse of the third tangent with the right line which
passes through the two given points, draw an indefinite right line;
and, taking this line for the first ordinate radius, transform the
figure by the preceding Lemma into a new figure. In this figure those
two tangents will become parallel to each other, and the third tangent
will be parallel to the right line that passes through the two given
points.
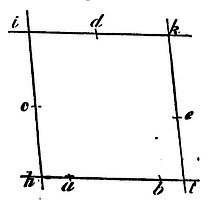 Suppose hi, kl to be
those two parallel tangents, ik the third tangent, and hl
a right line parallel thereto, passing through those points a, b,
through which the conic section ought to pass in this new figure; and
completing the parallelogram hikl, let the right lines hi,
ik, kl be so cut in c, d, e, that hc may be
to the square root of the rectangle ahb, ic, to id,
and ke to kd, as the sum of the right lines hi
and kl is to the sum of the three lines, the first whereof
is the right line ik, and the other two are the square roots
of the rectangles ahb and alb; and c, d, e,
will be the points of contact. For by the properties of the conic
sections, hc² to the rectangle ahb, and ic²
to id², and ke² to kd², and el²
to the rectangle alb, are all in the same ratio; and
therefore hc to the square root of ahb, ic to id,
ke to kd, and el to the square root of alb,
are in the subduplicate of that ratio; and by composition, in the
given ratio of the sum of all the antecedents hi + kl, to
the sum of all the consequents √(ahb)+ik+√(alb).
Wherefore from that given ratio we have the points of contact c,
d, e, in the new figure. By the inverted operations of the last
Lemma, let those points be transferred into the first figure, and the
trajectory will be there described by Prob. XIV. Q.E.F.
But according as the points a, b, fall between
the points h, l, or without them, the points c, d, e,
must be taken either between the points, h,
i, k, l, or without them. If one of the points a, b,
falls between the points h, i, and the other without the
points h, l, the Problem is impossible.
Suppose hi, kl to be
those two parallel tangents, ik the third tangent, and hl
a right line parallel thereto, passing through those points a, b,
through which the conic section ought to pass in this new figure; and
completing the parallelogram hikl, let the right lines hi,
ik, kl be so cut in c, d, e, that hc may be
to the square root of the rectangle ahb, ic, to id,
and ke to kd, as the sum of the right lines hi
and kl is to the sum of the three lines, the first whereof
is the right line ik, and the other two are the square roots
of the rectangles ahb and alb; and c, d, e,
will be the points of contact. For by the properties of the conic
sections, hc² to the rectangle ahb, and ic²
to id², and ke² to kd², and el²
to the rectangle alb, are all in the same ratio; and
therefore hc to the square root of ahb, ic to id,
ke to kd, and el to the square root of alb,
are in the subduplicate of that ratio; and by composition, in the
given ratio of the sum of all the antecedents hi + kl, to
the sum of all the consequents √(ahb)+ik+√(alb).
Wherefore from that given ratio we have the points of contact c,
d, e, in the new figure. By the inverted operations of the last
Lemma, let those points be transferred into the first figure, and the
trajectory will be there described by Prob. XIV. Q.E.F.
But according as the points a, b, fall between
the points h, l, or without them, the points c, d, e,
must be taken either between the points, h,
i, k, l, or without them. If one of the points a, b,
falls between the points h, i, and the other without the
points h, l, the Problem is impossible.
Proposition xxvi. Problem xviii.
To describe a trajectory that shall pass through a given point, and touch four right lines given by position.
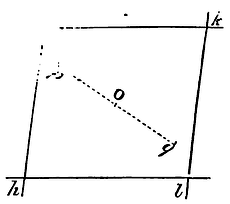
From the common intersections, of any two of the tangents to the common intersection of the other two, draw an indefinite right line; and taking this line for the first ordinate radius; transform the figure (by Lem. XXII) into a new figure, and the two pairs of tangents, each of which before concurred in the first ordinate radius, will now become parallel. Let hi and kl, ik and hl, be those pairs of parallels completing the parallelogram hikl. And let p be the point in this new figure corresponding to the given point in the first figure. Through O the centre of the figure draw pq: and Oq being equal to Op, q will be the other point through which the conic section must pass in this new figure. Let this point be transferred, by the inverse operation of Lem. XXII into the first figure, and there we shall have the two points through which the trajectory is to be described. But through those points that trajectory may be described by Prop. XVII.
Lemma xxiii.
If two right lines, as AC, BD given by position, and terminating in given points A, B, are in a given ratio one to the other, and the right line CD, by which the indetermined points C, D are joined is cut in K in a given ratio; I say, that the point K will be placed in a right line given by position.
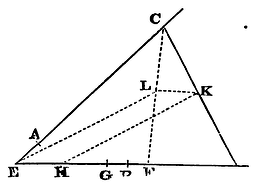
For let the right lines AC, BD meet in E, and in BE take BG to AE as BD is to AC, and let FD be always equal to the given line EG; and, by construction, EC will be to GD, that is, to EF, as AC to BD, and therefore in a given ratio; and therefore the triangle EFC will be given in kind. Let CF be cut in L so as CL may be to CF in the ratio of CK to CD; and because that is a given ratio, the triangle EFL will be given in kind, and therefore the point L will be placed in the right line EL given by position. Join LK, and the triangles CLK, CFD will be similar; and because FD is a given line, and LK is to FD in a given ratio, LK will be also given. To this let EH be taken equal, and ELKH will be always a parallelogram. And therefore the point K is always placed in the side HK (given by position) of that parallelogram. Q.E.D.
Cor. Because the figure EFLC is given in kind, the three right lines EF, EL, and EC, that is, GD, HK, and EC, will have given ratios to each other.
Lemma xxiv.
If three right lines, two whereof are parallel, and given by position, touch any conic section; I say, that the semi-diameter of the section which is parallel to those two is a mean proportional between the segments of those two that are intercepted between the points of contact and the third tangent.
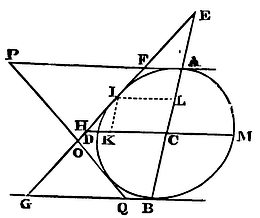
Let AF, GB be the two parallels touching the conic section ADB in A and B; EF the third right line touching the conic section in I, and meeting the two former tangents in F and G, and let CD be the semi-diameter of the figure parallel to those tangents; I say, that AF, CD, BG are continually proportional.
For if the conjugate diameters AB, DM meet the tangent FG in E and H, and cut one the other in C, and the parallelogram IKCL be completed; from the nature of the conic sections, EC will be to CA as CA to CL; and so by division, EC − CA to CA − CL, or EA to AL; and by composition, EA to EA + AL or EL, as EC to EC + CA or EB; and therefore (because of the similitude of the triangles EAF, ELI, ECH, EBG) AF is to LI as CH to BG. Likewise, from the nature of the conic sections, LI (or CK) is to CD as CD to CH; and therefore (ex aequo perturbatè) AF is to CD as CD to BG. Q.E.D.
Cor. 1. Hence if two tangents FG, PQ, meet two parallel tangents AF, BG in F and G, P and Q, and cut one the other in O; AF (ex aequo perturbatè) will be to BQ as AP to BG, and by division, as FP to GQ, and therefore as FO to OG.
Cor. 2. Whence also the two right lines PG, FQ drawn through the points P and G, F and Q, will meet in the right line ACB passing through the centre of the figure and the points of contact A, B.
Lemma xxv.
If four sides of a parallelogram indefinitely produced touch any conic section, and are cut by a fifth tangent; I say, that, taking those segments of any two conterminous sides that terminate in opposite angles of the parallelogram, either segment is to the side from which it is cut off as that part of the other conterminous side which is intercepted between the point of contact and the third side is to the other segment.
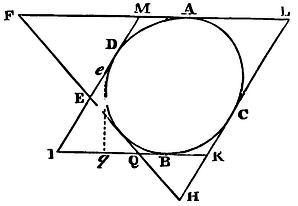
Let the four sides ML, IK, KL, MI, of the parallelogram MLIK touch the F conic section in A, B, C, D; and let the fifth tangent FQ cut those sides in F, Q, H, and E; and taking the segments ME, KQ of the sides MI, KI, or the segments KH, MF of the sides KL, ML; I say, that ME is to MI as BK to KQ; and KH to KL as AM to MF. For, by Cor. 1 of the preceding Lemma, ME is to EI as (AM or) BK to BQ; and, by composition, ME is to MI as BK to KQ. Q.E.D. Also KH is to HL as (BK or) AM to AF; and by division, KH to KL as AM to MF. Q.E.D.
Cor. 1. Hence if a parallelogram IKLM described about a given conic section is given, the rectangle KQ x ME, as also the rectangle KH x MF equal thereto, will be given. For, by reason of the similar triangles KQH, MFE, those rectangles are equal.
Cor. 2. And if a sixth tangent eq is drawn meeting the tangents KI, MI in q and e, the rectangle KQ x ME will be equal to the rectangle Kq x Me, and KQ will be to Me as Kq to ME, and by division as Qq to Ee.
Cor. 3. Hence, also, if Eq, eQ, are joined and bisected, and a right line is drawn through the points of bisection, this right line will pass through the centre of the conic section. For since Qq is to Ee as KQ to Me, the same right line will pass through the middle of all the lines Eq, eQ, MK (by Lem. XXIII), and the middle point of the right line MK is the centre of the section.
Proposition xxvii. Problem xix.
To describe a trajectory that may touch five right lines given by position.
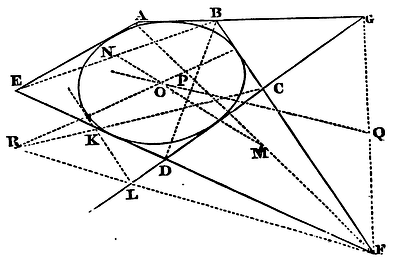
Supposing ABG, BCF, GCD, FDE, EA to be the tangents given by position. Bisect in M and N, AF, BE, the diagonals of the quadrilateral figure ABFE contained under any four of them; and (by Cor. 3, Lem. XXV) the right line MN drawn through the points of bisection will pass through the centre of the trajectory. Again, bisect in P and Q, the diagonals (if I may so call them) BD, GF of the quadrilateral figure BGDF contained under any other four tangents, and the right line PQ, drawn through the points of bisection will pass through the centre of the trajectory; and therefore the centre will be given in the con course of the bisecting lines. Suppose it to be O. Parallel to any tangent BC draw KL at such distance that the centre O may be placed in the middle between the parallels; this KL will touch the trajectory to be described. Let this cut any other two tangents GCD, FDE, in L and K. Through the points C and K, F and L, where the tangents not parallel, GL, FK meet the parallel tangents OF, KL, draw OK, FL meeting in R; and the right line OR drawn and produced, will cut the parallel tangents CF, KL, in the points of contact. This appears from Cor. 2, Lem. XXIV. And by the same method the other points of contact may be found, and then the trajectory may be described by Prob. XIV. Q.E.F.
Scholium.
Under the preceding Propositions are comprehended those Problems wherein either the centres or asymptotes of the trajectories are given. For when points and tangents and the centre are given, as many other points and as many other tangents are given at an equal distance on the other side of the centre. And an asymptote is to be considered as a tangent, and its infinitely remote extremity (if we may say so) is a point of contact. Conceive the point of contact of any tangent removed in infinitum, and the tangent will degenerate into an asymptote, and the constructions of the preceding Problems will be changed into the constructions of those Problems wherein the asymptote is given.
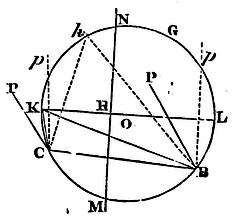
After the trajectory is described, we may find its axes and foci in this manner. In the construction and figure of Lem. XXI, let those legs BP, CP, of the moveable angles PBN, PCN, by the concourse of which the trajectory was described, be made parallel one to the other; and retaining that position, let them revolve about their poles B, C, in that figure. In the mean while let the other legs CN, BN, of those angles, by their concourse K or k, describe the circle BKGC. Let O be the centre of this circle; and from this centre upon the ruler MN, wherein those legs CN, BN did concur while the trajectory was described, let fall the perpendicular OH meeting the circle in K and L. And when those other legs CK, BK meet in the point K that is nearest to the ruler, the first legs CP, BP will be parallel to the greater axis, and perpendicular on the lesser; and the contrary will happen if those legs meet in the remotest point L. Whence if the centre of the trajectory is given; the axes will be given; and those being given, the foci will be readily found.
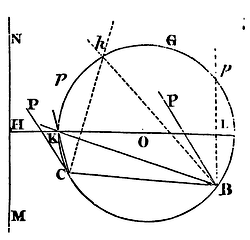
But the squares of the axes are one to the other as KH to LH, and thence it is easy to describe a trajectory given in kind through four given points. For if two of the given points are made the poles C, B, the third will give the moveable angles PCK, PBK; but those being given, the circle BGKC may be described. Then, because the trajectory is given in kind, the ratio of OH to OK, and therefore OH itself, will be given. About the centre O, with the interval OH, describe another circle, and the right line that touches this circle, and passes through the concourse of the legs CK, BK, when the first legs CK, BP meet in the fourth given point, will be the ruler MN, by means of which the trajectory may be described. Whence also on the other hand a trapezium given in kind (excepting a few cases that are impossible) may be inscribed in a given conic section.
There are also other Lemmas, by the help of which trajectories given in kind may be described through given points, and touching given lines. Of such a sort is this, that if a right line is drawn through any point given by position, that may cut a given conic section in two points, and the distance of the intersections is bisected, the point of bisection will touch another conic section of the same kind with the former, and having its axes parallel to the axes of the former. But I hasten to things of greater use.
Lemma xxvi.
To place the three angles of a triangle, given both in kind and magnitude, in respect of as many rigid lines given by position, provided they are not all parallel among themselves, in such manner that the several angles may touch the several lines.
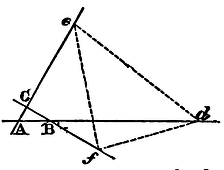
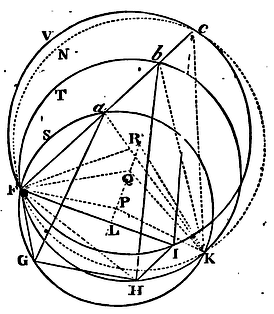
Three indefinite right lines AB, AC, BC, are given by position, and it is required so to place the triangle DEF that its angle D may touch the line AB, its angle E the line AC, and its angle F the line BC. Upon DE, DF, and EF, describe three segments of circles DRE, DGF, EMF, capable of angles equal to the angles BAC, ABC, ACB respectively. But those segments are to be described towards such sides of the lines DE, DF, EF, that the letters DRED may turn round about in the same order with the letters BACB; the letters DGFD in the same order with the letters ABCA; and the letters EMFE in the same order with the letters ACBA; then; completing those segments into entire circles let the two former circles cut one the other in G, and suppose P and Q, to be their centres. Then joining GP, PQ, take Ga to AB as GP is to PQ; and about the centre G, with the interval Ga, describe a circle that may cut the first circle DGE in a. Join aD cutting the second circle DFG in b, as well as aE cutting the third circle EMF in c. Complete the figure ABCdef similar and equal to the figure abcDEF: I say, the thing is done.
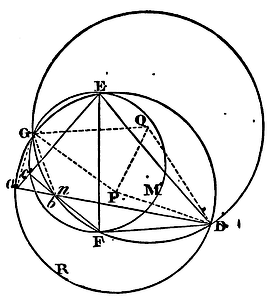
For drawing Fc meeting aD in n, and joining aG, bG, QG, QD, PD, by construction the angle EaD is equal to the angle CAB, and the angle acF equal to the angle ACB; and therefore the triangle anc equiangular to the triangle ABC. Wherefore the angle anc or FnD is equal to the angle ABC, and consequently to the angle FbD; and therefore the point n falls on the point b. Moreover the angle GPQ, which is half the angle GPD at the centre, is equal to the angle GaD at the circumference; and the angle GQP, which is half the angle GQD at the centre, is equal to the complement to two right angles of the angle GbD at the circumference, and therefore equal to the angle Gba. Upon which account the triangles GPQ, Gab, are similar, and Ga is to ab as GP to PQ; that is (by construction), as Ga to AB. Wherefore ab and AB are equal; and consequently the triangles abc, ABC, which we have now proved to be similar, are also equal. And therefore since the angles D, E, F, of the triangle DEF do respectively touch the sides ab, ac, bc of the triangle abc, the figure ABCdef may be completed similar and equal to the figure abcDEF, and by completing it the Problem will be solved. Q.E.F.
Cor. Hence a right line may be drawn whose parts given in length may be intercepted between three right lines given by position. Suppose the triangle DEF, by the access of its point D to the side EF, and by having the sides DE, DF placed in directum to be changed into a right line whose given part DE is to be interposed between the right lines AB, AC given by position; and its given part DF is to be interposed between the right lines AB, BC, given by position; then, by applying the preceding construction to this case; the Problem will be solved.
Proposition xxviii. Problem xx.
To describe a trajectory given both in kind and magnitude, given parts of which shall be interposed between three right lines given by position.
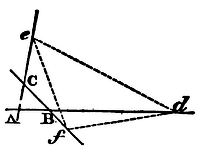
Suppose a trajectory is to be described that may be similar and equal to the curve line DEF, and may be cut by three right lines AB, AC, BC, given by position, into parts DE and EF, similar and equal to the given parts of this curve line.
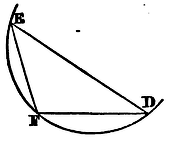
Draw the right lines DE, EP, DF: and place the angles D, E, F, of this triangle DEF, so as to touch those right lines given by position (by Lem. XXVI). Then about the triangle describe the trajectory, similar and equal to the curve DEF. Q.E.F.
Lemma xxvii.
To describe a trapezium given in kind, the angles whereof may be so placed, in respect of four right lines given by position, that are neither all parallel among themselves, nor converge to one common point, that the several angles may touch the several lines.
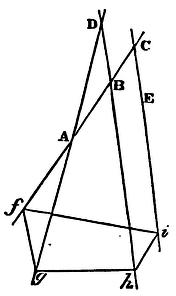
Let the four right lines ABC, AD, BD, CE, be given by position; the
first cutting the second in A, the third in B, and the fourth in C;
and suppose a trapezium fghi is to be described that may be
similar to the trapezium FGHI, and whose angle f, equal to
the given angle F, may touch the right line ABC; and the other angles
g, h, i, equal to the other given angles, G, H, I, may touch
the other lines AD, BD, CE, respectively. Join FH, and upon FG, FH, FI
describe as many segments of circles FSG, FTH, FVI, the first of which
FSG may be capable of an angle equal to the angle BAD; the second FTH
capable of an angle equal to the angle CBD; and the third FVI of an
angle equal to the angle ACE. But the segments are to be described
towards those sides of the lines FG, FH, FI, that the circular order
of the letters FSGF may be the same as of the letters BADB, and that
the letters FTHF may turn about in the same order as the letters CBDC
and the letters FVIF in the game order as the letters ACEA. Complete
the segments into entire circles, and let P be the centre of the first
circle FSG, Q the centre of the second FTH. Join and produce both ways
the line PQ, and in it take QR in the same ratio to PQ as BC has to
AB. But QR is to be taken towards that side of the point Q, that the
order of the letters P, Q, R
 may be the same as of the letters A, B, C; and about the centre R with
the interval RF describe a fourth circle FNc cutting the
third circle FVI in c. Join Fc cutting the first
circle in a, and the second in b. Draw aG,
bH, cI, and let the figure ABCfghi be made
similar to the figure abcFGHI; and the trapezium fghi
will be that which was required to be described.
may be the same as of the letters A, B, C; and about the centre R with
the interval RF describe a fourth circle FNc cutting the
third circle FVI in c. Join Fc cutting the first
circle in a, and the second in b. Draw aG,
bH, cI, and let the figure ABCfghi be made
similar to the figure abcFGHI; and the trapezium fghi
will be that which was required to be described.
For let the two first circles FSG, FTH cut one the other in K; join PK, QK, RK, aK, bK, cK, and produce QP to L. The angles FaK, FbK, FcK at the circumferences are the halves of the angles FPK, FQK, FRK, at the centres, and therefore equal to LPK, LQK, LRK, the halves of those angles. Wherefore the figure PQRK is equiangular and similar to the figure abcK, and consequently ab is to bc as PQ to QR, that is, as AB to BC. But by construction, the angles fAg, fBh, fCi, are equal to the angles FaG, FbH, FcI. And therefore the figure ABCfghi may be completed similar to the figure abcFGHI. Which done a trapezium fghi will be constructed similar to the trapezium FGHI, and which by its angles f, g, h, i will touch the right lines ABC, AD, BD, CE. Q.E.F.
Cor. Hence a right line may be drawn whose parts intercepted in a given order, between four right lines given by position, shall have a given proportion among themselves. Let the angles FGH, GHI, be so far increased that the right lines FG, GH, HI, may lie in directum; and by constructing the Problem in this case, a right line fghi will be drawn, whose parts fg, gh, hi, intercepted between the four right lines given by position, AB and AD, AD and BD, BD and CE, will be one to another as the lines FG, GH, HI, and will observe the same order among them selves. But the same thing may be more readily done in this manner.
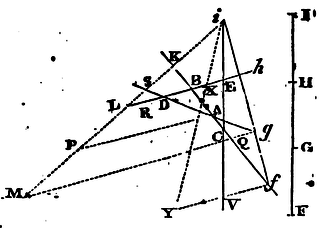
Produce AB to K and BD to L, so as BK may be to AB as HI to GH; and DL to BD as GI to FG; and join KL meeting the right line CE in i. Produce iL to M, so as LM may be to iL as GH to HI; then draw MQ parallel to LB, and meeting the right line AD in g, and join gi cutting AB, BD in f, h; I say, the thing is done.
For let Mg cut the right line AB in Q, and AD the right line KL in S, and draw AP parallel to BD, and meeting iL in P, and gM to Lh (gi to hi, Mi to Li, GI to HI, AK to BK) and AP to BL, will be in the same ratio. Cut DL in R, so as DL to RL may be in that same ratio; and because gS to gM, AS to AP, and DS to DL are proportional; therefore (ex aequo) as gS to Lh, so will AS be to BL, and DS to RL; and mixtly, BL − RL to Lh − BL, as AS − DS to gS − AS. That is, BR is to Bh as AD is to Ag, and therefore as BD to gQ. And alternately BR is to BD as Bh to gQ, or as fh to fg. But by construction the line BL was cut in D and R in the same ratio as the line FI in G and H; and therefore BR is to BD as FH to FG. Wherefore fh is to fg as FH to FG. Since, therefore, gi to hi likewise is as Mi to Li, that is, as GI to HI, it is manifest that the lines FI, fi, are similarly cut in G and H, g and h. Q.E.F.
In the construction of this Corollary, after the line LK is drawn cutting CE in i, we may produce iE to V, so as EV may be to Ei as FH to HI, and then draw Vf parallel to BD. It will come to the same, if about the centre i with an interval IH, we describe a circle cutting BD in X, and produce iX to Y so as iY may be equal to IF, and then draw Yf parallel to BD.
Sir Christopher Wren and Dr. Wallis have long ago given other solutions of this Problem.
Proposition xxix. Problem xxi.
To describe a trajectory given in kind, that may be cut by four right lines given by position, into parts given in order, kind, and proportion.
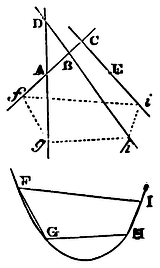
Suppose a trajectory is to be described that may be similar to the curve line FGHI, and whose parts, similar and proportional to the parts FG, GH, HI of the other, may be intercepted between the right lines AB and AD, AD, and BD, BD and CE given by position, viz., the first between the first pair of those lines, the second between the second, and the third between the third. Draw the right lines FG, GH, HI, FI; and (by Lem. XXVII) describe a trapezium fghi that may be similar to the trapezium FGHI, and whose angles f, g, h, i, may touch the right lines given by position AB, AD, BD, CE, severally according to their order. And then about this trapezium describe a trajectory, that trajectory will be similar to the curve line FGHI.
Scholium.
This problem may be likewise constructed in the following manner.
Joining FG, GH, HI, FI, produce GF to V, and join FH, IG, and make
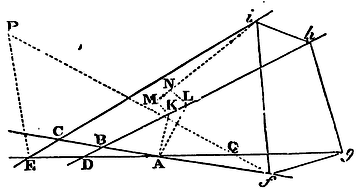 the angles CAK, DAL equal to the
angles FGH, VFH. Let AK, AL meet the right line BD in K and L, and
thence draw KM, LN, of which let KM make the angle AKM equal to the
angle GHI, and be itself to AK as HI is to GH; and let LN make the
angle ALN equal to the angle FHI, and be itself to AL as HI to FH.
the angles CAK, DAL equal to the
angles FGH, VFH. Let AK, AL meet the right line BD in K and L, and
thence draw KM, LN, of which let KM make the angle AKM equal to the
angle GHI, and be itself to AK as HI is to GH; and let LN make the
angle ALN equal to the angle FHI, and be itself to AL as HI to FH.
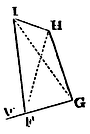 But AK, KM. AL, LN are to be drawn towards
those sides of the lines AD, AK, AL, that the letters CAKMC, ALKA,
DALND may be carried round in the same order as the letters FGHIF; and
draw MN meeting the right line CE in i. Make the angle iEP
equal to the angle IGF, and let PE be to Ei as FG to GI; and
through P draw PQf that may with the right line ADE contain
an angle PQE equal to the angle FIG, and may meet the right line AB in
f, and join fi. But PE and PQ are to be drawn
towards those sides of the lines CE, PE, that the circular order of
the letters PEiP and PEQP may be the same as of the letters
FGHIF; and if upon the line fi, in the same order of
letters, and similar to the trapezium FGHI, a trapezium fghi
is constructed, and a trajectory given in kind is circumscribed about
it, the Problem will be solved.
But AK, KM. AL, LN are to be drawn towards
those sides of the lines AD, AK, AL, that the letters CAKMC, ALKA,
DALND may be carried round in the same order as the letters FGHIF; and
draw MN meeting the right line CE in i. Make the angle iEP
equal to the angle IGF, and let PE be to Ei as FG to GI; and
through P draw PQf that may with the right line ADE contain
an angle PQE equal to the angle FIG, and may meet the right line AB in
f, and join fi. But PE and PQ are to be drawn
towards those sides of the lines CE, PE, that the circular order of
the letters PEiP and PEQP may be the same as of the letters
FGHIF; and if upon the line fi, in the same order of
letters, and similar to the trapezium FGHI, a trapezium fghi
is constructed, and a trajectory given in kind is circumscribed about
it, the Problem will be solved.
So far concerning the finding of the orbits. It remains that we determine the motions of bodies in the orbits so found.