The Mathematical Principles
of
Natural Philosophy
Book 3.3
C®pyRight & C©pyLeft
by
Sir Isaac Newton
Translated into English by Andrew Motte
Last Update: 11 January 1666
Table of Contents
The Mathematical Principles of Natural Philosophy
by Isaac Newton
Book 3.3
The former part of this Proposition appears from Phaen. I, and Prop. II
or III, Book I; the latter from Phaen. I, and Cor. 6, Prop. IV, of the same Book.
The same thing we are to understand of the planets which encompass
Saturn, by Phaen. II.
The former part of the Proposition is manifest from Phaen. V, and Prop.
II, Book I; the latter from Phaen. IV, and Cor. 6, Prop. IV,
of the same Book. But this part of the Proposition is, with great
accuracy, demonstrable from the quiescence of the aphelion points; for a
very small aberration from the reciprocal duplicate proportion
would (by Cor. 1, Prop. XLV, Book I) produce a motion of the apsides
sensible enough in every single revolution, and in many of them
enormously great.
The former part of the Proposition is evident from Phaen. VI, and Prop.
II or III, Book I; the latter from the very slow motion of the moon's
apogee; which in every single revolution amounting but to 3° 3′ in
consequentia, may be neglected. For (by Cor. 1. Prop. XLV, Book
I) it appears, that, if the distance of the moon from the earth's centre
is to the semi-diameter of the earth as D to 1, the force, from which
such a motion will result, is reciprocally as D²
4/243,
i. e., reciprocally as the power of D,
whose exponent is 24/243;
that is to say, in the proportion of the distance something greater than
reciprocally duplicate, but which comes 59¾ times nearer to the
duplicate than to the triplicate proportion. But in regard that this
motion is owing to the action of the sun (as we shall afterwards
shew), it is here to be neglected. The action of the
sun, attracting the moon from the earth, is nearly as the moon's
distance from the earth; and therefore (by what we have shewed in Cor.
2, Prop. XLV, Book I) is to the centripetal force of the moon as 2 to
357,45, or nearly so; that is,
as 1 to 17829/40.
And if we neglect so inconsiderable a force of the sun, the remaining
force, by which the moon is retained in its orb, will be reciprocally as
D². This will yet more fully appear from comparing this force with the
force of gravity, as is done in the next Proposition.
Cor. If we augment the mean centripetal force
by which the moon is retained in its orb, first in the proportion of 177
29/40 to
17829/40,
and then in the duplicate proportion of the semi-diameter of the earth
to the mean distance of the centres of the moon and earth, we shall have
the centripetal force of the moon at the surface of the earth; supposing
this force, in descending to the earth's surface, continually to
increase in the reciprocal duplicate proportion of the height.
The mean distance of the moon from the earth in the syzygies in
semi-diameters of the earth, is, according to Ptolemy and most
astronomers, 59; according to Vendelin and Huygens,
60; to Copernicus, 60⅓; to Street,
602/5;
and to Tycho, 56½. But Tycho, and all that follow
his tables of refraction, making the refractions of the sun and moon
(altogether against the nature of light) to exceed the refractions of
the fixed stars, and that by four or five minutes near the horizon,
did thereby increase the moon's horizontal parallax by a like
number of minutes, that is, by a twelfth or fifteenth part of the whole
parallax. Correct this error, and the distance will become about 60½
semi-diameters of the earth, near to what others have assigned. Let us
assume the mean distance of 60 diameters in the syzygies; and suppose
one revolution of the moon, in respect of the fixed stars, to be
completed in 27d.7h.43′, as astronomers have
determined; and the circumference of the earth to amount to 123249600 Paris
feet, as the French have found by mensuration. And now if we imagine the
moon, deprived of all motion, to be let go, so as to descend towards the
earth with the impulse of all that force by which (by Cor. Prop. III) it
is retained in its orb, it will in the space of one minute of time,
describe in its fall 151/12
Paris feet. This we gather by a calculus, founded either upon
Prop. XXXVI, Book I, or (which comes to the same thing) upon Cor. 9,
Prop. IV, of the same Book. For the versed sine of that arc, which the
moon, in the space of one minute of time,
would by its mean motion
describe at the distance of 60 semi-diameters of the earth, is nearly 15
1/12 Paris feet,
or more accurately 15 feet, 1 inch,
and 1 line 4/9.
Where fore, since that force, in approaching to the earth, increases in
the reciprocal duplicate proportion of the distance, and, upon that
account, at the surface of the earth, is 60 x 60 times greater than at
the moon, a body in our regions, falling with that force, ought in the
space of one minute of time,
to describe 60 x 60 x 151/12
Paris feet; and, in the space of one second of time, to
describe 151/12 of those
feet; or more accurately 15 feet, 1 inch,
and 1 line 4/9.
And with this very force we actually find that bodies here upon earth do
really descend; for a pendulum oscillating seconds in the latitude of
Paris will be 3 Paris feet, and 8 lines ½ in length, as Mr. Huygens
has observed. And the space which a heavy body describes by falling in
one second of time is to half the length of this pendulum in the
duplicate ratio of the circumference of a circle to its diameter (as Mr.
Huygens has also shewn), and is therefore 15 Paris
feet, 1 inch, 1 line 7/9.
And therefore the force by which the moon is retained in its orbit
becomes, at the very surface of the earth, equal to the force of gravity
which we observe in heavy bodies there. And therefore (by Rule I and II)
the force by which the moon is retained in its orbit is that very same
force which we commonly call gravity; for, were gravity another force
different from that, then bodies descending to the earth with the joint
impulse of both forces would fall with a double velocity, and in the
space of one second of time would describe 301/6
Paris feet; altogether against experience.
This calculus is founded on the hypothesis of the earth's standing
still; for if both earth and moon move about the sun, and at the same
time about their common centre of gravity, the distance of the centres
of the moon and earth from one another will be 60½ semi-diameters of the
earth; as may be found by a computation from Prop. LX, Book I.
The demonstration of this Proposition may be more diffusely explained
after the following manner. Suppose several moons to revolve about the
earth, as in the system of Jupiter or Saturn: the periodic times of
these moons (by the argument of induction) would observe the same law
which Kepler found to obtain among the planets; and therefore
their centripetal forces would be reciprocally as the squares of the
distances from the centre of the earth, by Prop. I, of this Book. Now if
the lowest of these were very small, and were so near the earth as
almost to touch the tops of the highest mountains, the centripetal force
thereof, retaining it in its orb, would be very nearly equal to the
weights of any terrestrial bodies that should be found upon
the tops of those mountains, as may be known by the foregoing
computation. Therefore if the same little moon should be deserted by its
centrifugal force that carries it through its orb;
and so be disabled
from going onward therein, it would descend to the earth; and that with
the same velocity as heavy bodies do actually fall with upon the tops of
those very mountains; because of the equality of the forces that oblige
them both to descend. And if the force by which that lowest moon would
descend were different from gravity, and if that moon were to gravitate
towards the earth, as we find terrestrial bodies do upon the tops of
mountains, it would then descend with twice the velocity, as being impel
led by both these forces conspiring together. Therefore since both these
forces, that is, the gravity of heavy bodies, and the centripetal forces
of the moons, respect the centre of the earth, and are similar and equal
between themselves, they will (by Rule I and II) have one and the same
cause. And therefore the force which retains the moon in its orbit is
that very force which we commonly call gravity; because otherwise this
little moon at the top of a mountain must either be without gravity, or
fall twice as swiftly as heavy bodies are wont to do.
For the revolutions of the circumjovial planets about Jupiter, of the
circumsaturnal about Saturn, and of Mercury and Venus, and the other
circumsolar planets, about the sun, are appearances of the same sort
with the revolution of the moon about the earth; and therefore, by Rule
II, must be owing to the same sort of causes; especially since it has
been demonstrated, that the forces upon which those revolutions depend
tend to the centres of Jupiter, of Saturn, and of the sun; and that
those forces, in receding from Jupiter, from Saturn, and from the sun,
decrease in the same proportion, and according to the same law, as the
force of gravity does in receding from the earth.
Cor. 1. There is, therefore, a power of gravity
tending to all the planets; for, doubtless, Venus, Mercury, and the
rest, are bodies of the same sort with Jupiter and Saturn. And since all
attraction (by Law III) is mutual, Jupiter will therefore gravitate
towards all his own satellites, Saturn towards his, the earth towards
the moon, and the sun towards all the primary planets.
Cor. 2. The force of gravity which tends to any
one planet is reciprocally as the square of the distance of places from
that planet's centre.
Cor. 3. All the planets do mutually gravitate
towards one another, by Cor. 1 and 2. And hence it is that Jupiter and
Saturn, when near their conjunction; by their
mutual attractions sensibly disturb each other's motions. So the sun
disturbs the motions of the moon; and both sun and moon disturb our sea,
as we shall hereafter explain.
The force which retains the celestial bodies in their orbits has been
hitherto called centripetal force; but it being now made plain that it
can be no other than a gravitating force, we shall hereafter call it
gravity. For the cause of that centripetal force which retains the moon
in its orbit will extend itself to all the planets, by Rule I, II, and
IV.
It has been, now of a long time, observed by others, that all sorts of
heavy bodies (allowance being made for the inequality of retardation
which they suffer from a small power of resistance in the air) descend
to the earth from equal heights in equal times; and that
equality of times we may distinguish to a great accuracy, by the help of
pendulums. I tried the thing in gold, silver, lead, glass, sand, common
salt, wood, water, and wheat. I provided two wooden boxes, round and
equal: I filled the one with wood, and suspended an equal weight of gold
(as exactly as I could) in the centre of oscillation of the other. The
boxes hanging by equal threads of 11 feet made a couple of pendulums
perfectly equal in weight and figure, and equally receiving the
resistance of the air. And, placing the one by the other, I observed
them to play together forward and backward, for a long time, with equal
vibrations. And therefore the quantity of matter in the gold (by Cor. 1
and 6, Prop. XXIV, Book II) was to the quantity of matter in the wood as
the action of the motive force (or vis motrix) upon all the
gold to the action of the same upon all the wood: that is, as the weight
of the one to the weight of the other: and the like happened in the
other bodies. By these experiments, in bodies of the same weight, I
could manifestly have discovered a difference of matter less than the
thousandth part of the whole, had any such been. But, without all doubt,
the nature of gravity towards the planets is the same as towards the
earth. For, should we imagine our terrestrial bodies removed to the orb
of the moon, and there, together with the moon, deprived of all motion,
to be let go, so as to fall together towards the earth, it is certain,
from what we have demonstrated before, that, in equal times, they would
describe equal spaces with the moon, and of consequence are to the moon,
in quantity of matter, as their weights to its weight. Moreover, since
the satellites of Jupiter perform their
revolutions in times which observe the sesquiplicate proportion of their
distances from Jupiter's centre, their accelerative gravities towards
Jupiter will be reciprocally as the squares of their distances from
Jupiter's centre; that is, equal, at equal distances. And, therefore,
these satellites, if supposed to fall towards Jupiter from
equal heights, would describe equal spaces in equal times, in like
manner as heavy bodies do on our earth. And, by the same argument, if
the circumsolar planets were supposed to be let fall at equal distances
from the sun, they would, in their descent towards the sun, describe
equal spaces in equal times. But forces which equally accelerate unequal
bodies must be as those bodies: that is to say, the weights of the
planets towards the sun, must be as their quantities of
matter. Further, that the weights of Jupiter and of his satellites
towards the sun are proportional to the several quantities of their
matter, appears from the exceedingly regular motions of the satellites
(by Cor. 3, Prop. LXV, Book 1). For if some of those bodies were more
strongly attracted to the sun in proportion to their quantity of matter
than others, the motions of the satellites would be disturbed by that
inequality of attraction (by Cor. 2, Prop. LXV, Book I). If, at equal
distances from the sun, any satellite, in proportion to the quantity of
its matter, did gravitate towards the sun with a force greater than
Jupiter in proportion to his, according to any given proportion, suppose
of d to e; then the distance between the centres of
the sun and of the satellite's orbit would be always greater than the
distance between the centres of the sun and of Jupiter nearly in the
subduplicate of that proportion: as by some computations I have found.
And if the satellite did gravitate towards the sun with a force, lesser
in the proportion of e to d, the distance of the
centre of the satellite's orb from the sun would be less than the
distance of the centre of Jupiter from the sun in the subduplicate of
the same proportion. Therefore if, at equal distances from the sun, the
accelerative gravity of any satellite towards the sun were greater or
less than the accelerative gravity of Jupiter towards the sun but by one
1/1000 part of the whole
gravity, the distance of the centre of the satellite's orbit from the
sun would be greater or less than the distance of Jupiter from the sun
by one 1/2000 part of
the whole distance; that is, by a fifth part of the distance of the
utmost satellite from the centre of Jupiter; an eccentricity of the
orbit which would be very sensible. But the orbits of the satellites are
concentric to Jupiter, and therefore the accelerative gravities of
Jupiter, and of all its satellites towards the sun, are equal among
themselves. And by the same argument, the weights of Saturn and of his
satellites towards the sun, at equal distances from the sun, are as
their several quantities of matter; and the weights of the moon and of
the earth towards the sun are either none, or accurately proportional to
the masses of matter which they contain. But some they are, by Cor. 1
and 3, Prop. V.
But further; the weights of all the parts of every planet towards any
other planet are one to another as the matter
in the several parts; for if some parts did gravitate more, others less,
than for the quantity of their matter, then the whole planet, according
to the sort of parts with which it most abounds, would gravitate more or
less than in proportion to the quantity of matter in the whole. Nor is
it of any moment whether these parts are external or internal; for if,
for example, we should imagine the terrestrial bodies with us to be
raised up to the orb of the moon, to be there compared with its body: if
the weights of such bodies were to the weights of the external parts of
the moon as the quantities of matter in the one and in the other
respectively; but to the weights of the internal parts in a greater or
less proportion, then likewise the weights of those bodies would be to
the weight of the whole moon in a greater or less proportion; against
what we have shewed above.
Cor. 1. Hence the weights of bodies do not
depend upon their forms and textures; for if the weights could be
altered with the forms, they would be greater or less, according to the
variety of forms, in equal matter; altogether against experience.
Cor. 2. Universally, all bodies about the earth
gravitate towards the earth; and the weights of all, at equal distances
from the earth's centre, are as the quantities of matter which they
severally contain. This is the quality of all bodies within the reach of
our experiments; and therefore (by Rule III) to be affirmed of all
bodies whatsoever. If the aether, or any other body, were
either altogether void of gravity, or were to gravitate less in
proportion to its quantity of matter, then, because (according to Aristotle,
Des Cartes, and others) there is no diiference betwixt that and
other bodies but in mere form of matter, by a successive
change from form to form, it might be changed at last into a body of the
same condition with those which gravitate most in proportion to their
quantity of matter; and, on the other hand, the heaviest bodies,
acquiring the first form of that body, might by degrees quite lose their
gravity. And therefore the weights would depend upon the forms of
bodies, and with those forms might be changed: contrary to what was
proved in the preceding Corollary.
Cor. 3. All spaces are not equally full; for if
all spaces were equally full, then the specific gravity of the fluid
which fills the region of the air, on account of the extreme density of
the matter, would fall nothing short of the specific gravity of
quicksilver, or gold, or any other the most dense body; and, therefore,
neither gold, nor any other body, could descend in air; for bodies do
not descend in fluids, unless they are specifically heavier than the
fluids. And if the quantity of matter in a given space can, by any
rarefaction, be diminished, what should hinder a diminution to infinity?
Cor. 4. If all the solid particles of all
bodies are of the same density, nor can be rarefied without pores, a
void, space, or vacuum must be granted. By
bodies of the same density, I mean those whose vires inertiae,
are in the proportion of their bulks.
Cor. 5. The power of gravity is of a different
nature from the power of magnetism; for the magnetic attraction is not
as the matter attracted. Some bodies are attracted more by the magnet;
others less; most bodies not at all. The power of magnetism in one and
the same body may be increased and diminished; and is sometimes far
stronger, for the quantity of matter, than the power of gravity; and in
receding from the magnet decreases not in the duplicate but almost in
the triplicate proportion of the distance, as nearly as I could judge
from some rude observations.
That all the planets mutually gravitate one towards another, we have
proved before; as well as that the force of gravity towards every one of
them, considered apart, is reciprocally as the square of the distance of
places from the centre of the planet. And thence (by Prop. LXIX, Book I,
and its Corollaries) it follows, that the gravity tending towards all
the planets is proportional to the matter which they contain.
Moreover, since all the parts of any planet A gravitate towards any
other planet B; and the gravity of every part is to the gravity of the
whole as the matter of the part to the matter of the whole; and (by Law
III) to every action corresponds an equal re-action; therefore the
planet B will, on the other hand, gravitate towards all the parts of the
planet A; and its gravity towards any one part will be to the gravity
towards the whole as the matter of the part to the matter of the whole.
Q.E.D.
Cor. 1. Therefore the force of gravity towards
any whole planet arises from, and is compounded of, the forces of
gravity towards all its parts. Magnetic and electric attractions afford
us examples of this; for all attraction towards the whole arises from
the attractions towards the several parts. The thing may be easily
understood in gravity, if we consider a greater planet, as formed of a
number of lesser planets, meeting together in one globe; for hence
it would appear that the force of the whole must arise from the
forces of the component parts. If it is objected, that, according to
this law, all bodies with us must mutually gravitate one towards
another, whereas no such gravitation any where appears, I answer, that
since the gravitation towards these bodies is to the gravitation towards
the whole earth as these bodies are to the whole earth, the gravitation
towards them must be far less than to fall under the observation of our
senses.
Cor. 2. The force of gravity towards the
several equal particles of any body is reciprocally as the square of the
distance of places from the particles; as appears from Cor. 3, Prop.
LXXIV, Book I.
After I had found that the force of gravity towards a whole planet did
arise from and was compounded of the forces of gravity towards all its
parts, and towards every one part was in the reciprocal proportion of
the squares of the distances from the part, I was yet in doubt whether
that reciprocal duplicate proportion did accurately hold, or but nearly
so, in the total force compounded of so many partial ones; for it might
be that the proportion which accurately enough took place in greater
distances should be wide of the truth near the surface of the planet,
where the distances of the particles are unequal, and their situation
dissimilar. But by the help of Prop. LXXV and LXXVI, Book I, and their
Corollaries, I was at last satisfied of the truth of the Proposition, as
it now lies before us.
Cor. 1. Hence we may find and compare together
the weights of bodies towards different planets; for the weights of
bodies revolving in circles about planets are (by Cor. 2, Prop. IV, Book
I) as the diameters of the circles directly, and the squares of their
periodic times reciprocally; and their weights at the surfaces of the
planets, or at any other distances from their centres, are (by this
Prop.) greater or less in the reciprocal duplicate proportion of the
distances. Thus from the periodic times of Venus, revolving about the
sun, in 224d.16¾h, of the utmost circumjovial
satellite revolving about Jupiter, in 16d.168/15h.;
of the Huygenian satellite about Saturn in 15d.22⅔h.;
and of the moon about the earth in 27d.7h.43′;
compared with the mean distance of Venus from the sun, and with the
greatest heliocentric elongations of the outmost circumjovial satellite
from Jupiter's centre, 8′ 16″; of the Huygenian satellite from the
centre of Saturn, 3′4″; and of the moon from the earth, 10′33″: by
computation I found that the weight of equal bodies, at equal distances
from the centres of the sun, of Jupiter, of Saturn, and of the earth,
towards the sun, Jupiter, Saturn, and the earth, were one to another, as
1, 1/1067, 1/3021,
and 1/169282
respectively. Then because as the distances are increased or diminished,
the weights are diminished or increased in a duplicate ratio, the
weights of equal bodies towards the sun, Jupiter, Saturn, and the earth,
at the distances 10000, 997, 791, and 109 from their centres, that is,
at their very superficies, will be as 10000, 943, 529, and 435
respectively. How much the weights of bodies are at the superficies of
the moon, will be shewn hereafter.
Cor. 2. Hence likewise we discover the quantity
of matter in the several planets; for their
quantities of matter are as the forces of gravity at equal distances
from their centres; that is, in the sun, Jupiter, Saturn, and the earth,
as 1, 1/1067, 1/3021
and 1/169282
respectively. If the parallax of the sun be taken greater or less than
10″ 30‴, the quantity of matter in the earth must be augmented or
diminished in the triplicate of that proportion.
Cor. 3. Hence also we find the densities of the
planets; for (by Prop. LXXII, Book I) the weights of equal and similar
bodies towards similar spheres are, at the surfaces of those spheres, as
the diameters of the spheres and therefore the densities of dissimilar
spheres are as those weights applied to the diameters of the spheres.
But the true diameters of the Sun, Jupiter, Saturn, and the earth, were
one to another as 10000, 997, 791, and 109; and the weights towards the
same as 10000, 943, 529, and 435 respectively; and therefore their
densities are as 100, 94½, 67, and 400. The density of the earth, which
comes out by this computation, does not depend upon the parallax of the
sun, but is determined by the parallax of the moon, and therefore is
here truly defined. The sun, therefore, is a little denser than Jupiter,
and Jupiter than Saturn, and the earth four times denser than the sun;
for the sun, by its great heat, is kept in a sort of a rarefied state.
The moon is denser than the earth, as shall appear afterward.
Cor. 4. The smaller the planets are, they are,
caeteris paribus, of so much the greater density; for so the
powers of gravity on their several surfaces come nearer to equality.
They are likewise, caeteris paribus, of the greater density,
as they are nearer to the sun. So Jupiter is more dense than Saturn, and
the earth than Jupiter; for the planets were to be placed at different
distances from the sun, that, according to their degrees of density,
they might enjoy a greater or less proportion to the sun's heat. Our
water, if it were removed as far as the orb of Saturn, would be
converted into ice, and in the orb of Mercury would quickly fly away in
vapour; for the light of the sun, to which its heat is proportional, is
seven times denser in the orb of Mercury than with us: and by the
thermometer I have found that a sevenfold heat of our summer sun will
make water boil. Nor are we to doubt that the matter of Mercury is
adapted to its heat, and is therefore more dense than the matter of our
earth; since, in a denser matter, the operations of Nature require a
stronger heat.
If the matter of the planet were of an uniform density, this
Proposition would be accurately true (by Prop. LXXIII. Book I). The
error, therefore, can be no greater than what
may arise from the inequality of the density.
In the Scholium of Prop. XL, Book II, I have shewed that a globe of
water frozen into ice, and moving freely in our air, in the time that it
would describe the length of its semi-diameter, would lose by the
resistance of the air 1/4586
part of its motion; and the same proportion holds nearly in all globes,
how great soever, and moved with whatever velocity. But that our globe
of earth is of greater density than it would be if the whole consisted
of water only, I thus make out. If the whole consisted of water only,
whatever was of less density than water, because of its less specific
gravity, would emerge and float above. And upon this account, if a globe
of terrestrial matter, covered on all sides with water, was less dense
than water, it would emerge somewhere; and, the subsiding water falling
back, would be gathered to the opposite side. And such is the condition
of our earth, which in a great measure is covered with seas. The earth,
if it was not for its greater density, would emerge from the seas, and,
according to its degree of levity, would be raised more or less above
their surface, the water of the seas flowing backward to the opposite
side. By the same argument, the spots of the sun, which float upon the
lucid matter thereof, are lighter than that matter; and, however the
planets have been formed while they were yet in fluid masses, all the
heavier matter subsided to the centre. Since, therefore, the common
matter of our earth on the surface thereof is about twice as heavy as
water, and a little lower, in mines, is found about three, or four, or
even five times more heavy, it is probable that the quantity of the
whole matter of the earth may be five or six times greater than if it
consisted all of water; especially since I have before shewed that the
earth is about four times more dense than Jupiter. If, therefore,
Jupiter is a little more dense than water, in the space of thirty days,
in which that planet describes the length of 459 of its semi-diameters,
it would, in a medium of the same density with our air, lose almost a
tenth part of its motion. But since the resistance of mediums decreases
in proportion to their weight or density, so that water, which is 13
3/5 times lighter than
quicksilver, resists less in that proportion; and air, which is 860
times lighter than water, resists less in the same proportion; therefore
in the heavens, where the weight of the medium in which the planets move
is immensely diminished, the resistance will almost vanish.
It is shewn in the Scholium of Prop. XXII, Book II, that at the height
of 200 miles above the earth the air is more rare than it is at the
superficies of the earth in the ratio of 30 to 0,0000000000003998, or as
75000000000000 to 1 nearly. And hence the planet
Jupiter, revolving in a medium of the same density with that superior
air, would not lose by the resistance of the medium the 1000000th part
of its motion in 1000000 years. In the spaces near the earth the
resistance is produced only by the air, exhalations, and vapours. When
these are carefully exhausted by the air-pump from under the receiver,
heavy bodies fall within the receiver with perfect freedom, and without
the least sensible resistance: gold itself, and the lightest down, let
fall together, will descend with equal velocity; and though they fall
through a space of four, six, and eight feet, they will come to the
bottom at the same time; as appears from experiments. And therefore the
celestial regions being perfectly void of air and exhalations, the
planets and comets meeting no sensible resistance in those spaces will
continue their motions through them for an immense tract of time.
This is acknowledged by all, while some contend that the earth, others
that the sun, is fixed in that centre. Let us see what may from hence follow.
For (by Cor. 4 of the Laws) that centre either is at rest, or moves
uniformly forward in a right line; but if that centre moved, the centre
of the world would move also, against the Hypothesis.
For since (by Cor. 2, Prop. VIII) the quantity of matter in the sun is
to the quantity of matter in Jupiter as 1067 to 1; and the distance of
Jupiter from the sun is to the semi-diameter of the sun in a proportion
but a small matter greater, the common centre of gravity of Jupiter and
the sun will fall upon a point a little without the surface of the sun.
By the same argument, since the quantity of matter in the sun is to the
quantity of matter in Saturn as 3021 to 1, and the distance of Saturn
from the sun is to the semi-diameter of the sun in a proportion but a
small matter less, the common centre of gravity of Saturn and the sun
will fall upon a point a little within the surface of the sun. And,
pursuing the principles of this computation, we should find that though
the earth and all the planets were placed on one side of the sun, the
distance of the common centre of gravity of all from the centre of the
sun would scarcely amount to one diameter of the
sun. In other cases, the distances of those centres are always less; and
therefore, since that centre of gravity is in perpetual rest, the sun,
according to the various positions of the planets, must perpetually be
moved every way, but will never recede far from that centre.
Cor. Hence the common centre of gravity of the
earth, the sun, and all the planets, is to be esteemed the centre of the
world; for since the earth, the sun, and all the planets, mutually
gravitate one towards another, and are therefore, according to their
powers of gravity, in perpetual agitation, as the Laws of Motion
require, it is plain that their moveable centres can not be taken for
the immovable centre of the world. If that body were to be placed in the
centre, towards which other bodies gravitate most (according to common
opinion), that privilege ought to be allowed to the sun; but since the
sun itself is moved, a fixed point is to be chosen from which the centre
of the sun recedes least, and from which it would recede yet less if the
body of the sun were denser and greater, and therefore less apt to be
moved.
We have discoursed above of these motions from the Phaenomena. Now that
we know the principles on which they depend, from those principles we
deduce the motions of the heavens à priori. Because the
weights of the planets towards the sun are reciprocally as the squares
of their distances from the sun's centre, if the sun was at rest, and
the other planets did not mutually act one upon another, their orbits
would be ellipses, having the sun in their common focus; and they would
describe areas proportional to the times of description, by
Prop, I and XI, and Cor. 1, Prop. XIII, Book I. But the mutual actions
of the planets one upon another are so very small, that they may be
neglected; and by Prop. LXVI, Book I, they less disturb the motions of
the planets around the sun in motion than if those motions were
performed about the sun at rest.
It is true, that the action of Jupiter upon Saturn is not to be
neglected; for the force of gravity towards Jupiter is to the force of
gravity towards the sun (at equal distances, Cor. 2, Prop. VIII) as 1 to
1067; and therefore in the conjunction of Jupiter and Saturn, because
the distance of Saturn from Jupiter is to the distance of Saturn from
the sun almost as 4 to 9, the gravity of Saturn towards Jupiter will be
to the gravity of Saturn towards the sun as 81 to 16 x 1067; or, as 1 to
about 211. And hence arises a perturbation of the orb of Saturn in every
conjunction of this planet with Jupiter, so sensible, that astronomers
are puzzled with it. As the planet is
differently situated in these conjunctions, its eccentricity is
sometimes augmented, sometimes diminished; its aphelion is sometimes
carried forward, sometimes backward, and its mean motion is by turns
accelerated and retarded; yet the whole error in its motion about the
sun, though arising from so great a force, may be almost avoided (except
in the mean motion) by placing the lower focus of its orbit in the
common centre of gravity of Jupiter and the sun (according to Prop.
LXVII, Book I), and therefore that error, when it is greatest, scarcely
exceeds two minutes; and the greatest error in the mean motion scarcely
exceeds two minutes yearly. But in the conjunction of Jupiter and
Saturn, the accelerative forces of gravity of the sun towards Saturn, of
Jupiter towards Saturn, and of Jupiter towards the sun, are almost as
16,81, and 16 x 81 x 3021
25; or 156609: and therefore the
difference of the forces of gravity of the sun towards Saturn, and of
Jupiter towards Saturn, is to the force of gravity of Jupiter towards
the sun as 65 to 156609, or as 1 to 2409. But the greatest power of
Saturn to disturb the motion of Jupiter is proportional to this
difference; and therefore the perturbation of the orbit of Jupiter is
much less than that of Saturn's. The perturbations of the other orbits
are yet far less, except that the orbit of the earth is sensibly
disturbed by the moon. The common centre of gravity of the earth and
moon moves in an ellipsis about the sun in the focus thereof, and, by a
radius drawn to the sun, describes areas proportional to the times of
description. But the earth in the mean time by a menstrual motion is
revolved about this common centre.
The aphelions are immovable by Prop. XI, Book I; and so are the planes
of the orbits, by Prop. I of the same Book. And if the planes are fixed,
the nodes must be so too. It is true, that some inequalities may arise
from the mutual actions of the planets and comets in their revolutions;
but these will be so small, that they may be here passed by.
Cor. 1. The fixed stars are immovable, seeing
they keep the same position to the aphelions and nodes of the planets.
Cor. 2. And since these stars are liable to no
sensible parallax from the annual motion of the earth, they can have no
force, because of their immense distance, to produce any sensible effect
in our system. Not to mention that the fixed stars, every where
promiscuously dispersed in the heavens, by their contrary attractions
destroy their mutual actions, by Prop. LXX, Book I.
Since the planets near the sun (viz. Mercury, Venus, the Earth, and
Mars) are so small that they can act with but little
force upon each other, therefore their aphelions and nodes must be
fixed, excepting in so far as they are disturbed by the actions of
Jupiter and Saturn, and other higher bodies. And hence we may find, by
the theory of gravity, that their aphelions move a little in
consequentia, in respect of the fixed stars, and that in the
sesquiplicate proportion of their several distances from the sun. So
that if the aphelion of Mars, in the space of a hundred years, is
carried 33′ 20″ in consequentia, in respect of the fixed
stars; the aphelions of the Earth, of Venus, and of Mercury, will in a
hundred years be carried forwards 17′ 40″, 10′ 53″, and 4′ 16″,
respectively. But these motions are so inconsiderable, that we have
neglected them in this Proposition,
They are to be taken in the sub-sesquiplicate proportion of the
periodic times, by Prop. XV, Book I, and then to be severally augmented
in the proportion of the sum of the masses of matter in the sun and each
planet to the first of two mean proportionals betwixt that sum and the
quantity of matter in the sun, by Prop. LX, Book I.
This Problem is resolved by Prop. XVIII, Book I.
The Proposition is proved from the first Law of Motion, and Cor. 22,
Prop. LXVI, Book I. Jupiter, with respect to the fixed stars, revolves
in 9h.56′; Mars in 24h.39′; Venus in about 23h.;
the Earth in 23h.56′; the Sun in 25½ days, and the moon in 27
days, 7 hours, 43′. These things appear by the Phaenomena. The spots in
the sun's body return to the same situation on the sun's disk, with
respect to the earth, in 27½ days; and therefore with respect to the
fixed stars the sun revolves in about 25½ days. But because the lunar
day, arising from its uniform revolution about its axis, is menstrual, that
is, equal to the time of its periodic revolution in its orb,
therefore the same face of the moon will be always nearly turned to the
upper focus of its orb; but, as the situation of that focus requires,
will deviate a little to one side and to the other from the earth in the
lower focus; and this is the libration in longitude; for the libration
in latitude arises from the moon's latitude, and the inclination of its
axis to the plane of the ecliptic. This theory of the libration of the
moon, Mr. N. Mercator in his
Astronomy, published at the beginning of the year 1676, explained more
fully out of the letters I sent him. The utmost satellite of Saturn
seems to revolve about its axis with a motion like this of the moon,
respecting Saturn continually with the same face; for in its revolution
round Saturn, as often as it comes to the eastern part of its orbit, it
is scarcely visible, and generally quite disappears; which is like to be
occasioned by some spots in that part of its body, which is then turned
towards the earth, as M. Cassini has observed. So also the
utmost satellite of Jupiter seems to revolve about its axis with a like
motion, because in that part of its body which is turned from Jupiter it
has a spot, which always appears as if it were in Jupiter's own body,
whenever the satellite passes between Jupiter and our eye.
The equal gravitation of the parts on all sides would give a spherical
figure to the planets, if it was not for their diurnal revolution in a
circle. By that circular motion it comes to pass that the parts receding
from the axis endeavour to ascend about the equator; and therefore if
the matter is in a fluid state, by its ascent towards the equator it
will enlarge the diameters there, and by its descent towards the poles
it will shorten the axis. So the diameter of Jupiter (by the concurring
observations of astronomers) is found shorter betwixt pole and pole than
from east to west. And, by the same argument, if our earth was not
higher about the equator than at the poles, the seas would subside about
the poles, and, rising towards the equator, would lay all things there
under water.
Our countryman, Mr. Norwood, measuring a distance of 905751
feet of London measure between London and York,
in 1635, and observing the difference of latitudes to be 2° 28′,
determined the measure of one degree to be 367196 feet of London
measure, that is 57300 Paris toises. M. Picart,
measuring an arc of one degree, and 22′ 55″ of the meridian between Amiens
and Malvoisine, found an arc of one degree to be 57060 Paris
toises. M. Cassini, the father, measured the distance upon the
meridian from the town of Collioure in Roussillon to
the Observatory of Paris; and his son added the distance from
the Observatory to the Citadel of Dunkirk. The whole distance
was 486156½ toises and the difference of the latitudes of Collioure
and Dunkirk was 8 degrees, and 31′ 11
5/6″. Hence an arc of one
degree appears to be 57061 Paris toises. And from these
measures we conclude that the circumference of the earth is 123249600,
and its semi-diameter 19615800 Paris feet, upon the
supposition that the earth is of a spherical figure.
In the latitude of Paris a heavy body falling in a second of
time describes 15 Paris feet, 1 inch, 17/9
line, as above, that is, 2173 lines 7/9.
The weight of the body is diminished by the weight of the ambient air.
Let us suppose the weight lost thereby to be 1/11000
part of the whole weight; then that heavy body falling in vacua
will describe a height of 2174 lines in one second of time.
A body in every sidereal day of 23h.56′4″ uniformly
revolving in a circle at the distance of 19615800 feet from the centre,
in one second of time describes an arc of 1433,46 feet; the versed sine
of which is 0,05236561 feet, or 7,54064 lines. And therefore the force
with which bodies descend in the latitude of Paris is to the
centrifugal force of bodies in the equator arising from the diurnal
motion of the earth as 2174 to 7,54064.
The centrifugal force of bodies in the equator is to the centrifugal
force with which bodies recede directly from the earth in the latitude
of Paris 48° 50′ 10″ in the duplicate proportion of the radius
to the cosine of the latitude, that is, as 7,54064 to 3,267. Add this
force to the force with which bodies descend by their weight in the
latitude of Paris, and a body, in the latitude of Paris,
falling by its whole undiminished force of gravity, in the time of one
second, will describe 2177,267 lines, or 15 Paris feet, 1
inch, and 5,267 lines. And the total force of gravity in that latitude
will be to the centrifugal force of bodies in the equator of the earth
as 2177,267 to 7,54064, or as 289 to 1.
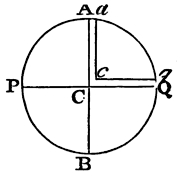
Wherefore if APBQ represent the figure of the earth, now no longer
spherical, but generated by the rotation of an ellipsis about its lesser
axis PQ; and ACQqca a canal full of water, reaching from the
pole Qq to the centre Cc, and thence rising to the
equator Aa; the weight of the water in the leg of the canal ACca
will be to the weight of water in the other leg QCcq as 289 to
288, because the centrifugal force arising from the circular motion
sustains and takes off one of the 289 parts of the weight (in the one
leg), and the weight of 288 in the other sustains the rest. But by
computation (from Cor. 2, Prop. XCI, Book I) I find, that, if the matter
of the earth was all uniform, and without any motion, and its axis PQ
were to the diameter AB as 100 to 101, the force of gravity in the place
Q towards the earth would be to the force of gravity in the same place Q
towards a sphere described about the centre C with the radius PC, or QC,
as 126 to 125. And, by the same argument, the force of gravity in the
place A towards the spheroid generated by the rotation of the
ellipsis APBQ about the axis AB is to the force of gravity in the same
place A, towards the sphere described about the centre C with the radius
AC, as 125 to 126. But the force of gravity in the place A towards the
earth is a mean proportional betwixt the forces of gravity towards the
spheroid and this sphere; because the sphere, by having its diameter PQ
diminished in the proportion of 101 to 100, is transformed into the
figure of the earth; and this figure, by having a third diameter
perpendicular to the two diameters AB and PQ diminished in the same
proportion, is converted into the said spheroid; and the force of
gravity in A, in either case, is diminished nearly in the same
proportion. Therefore the force of gravity in A towards the sphere
described about the centre C with the radius AC, is to the force of
gravity in A towards the earth as 126 to 125½. And the force of gravity
in the place Q towards the sphere described about the centre C with the
radius QC, is to the force of gravity in the place A towards the sphere
described about the centre C, with the radius AC, in the proportion of
the diameters (by Prop. LXXII, Book I), that is, as 100 to 101. If,
therefore, we compound those three proportions 126 to 125, 126 to 125½,
and 100 to 101, into one, the force of gravity in the place Q towards
the earth will be to the force of gravity in the place A towards the
earth as 126 x 126 x 100 to 125 x 125½ x 101; or as 501 to 500.
Now since (by Cor. 3, Prop. XCI, Book I) the force of gravity in either
leg of the canal ACca, or QCcq, is as the distance of
the places from the centre of the earth, if those legs are conceived to
be divided by transverse, parallel, and equidistant surfaces, into parts
proportional to the wholes, the weights of any number of parts in the
one leg ACca will be to the weights of the same number of parts
in the other leg as their magnitudes and the accelerative forces of
their gravity conjunctly, that is, as 101 to 100, and 500 to 501, or as
505 to 501. And therefore if the centrifugal force of every part in the
leg ACca, arising from the diurnal motion, was to the weight of
the same part as 4 to 505, so that from the weight of every part,
conceived to be divided into 505 parts, the centrifugal force might take
off four of those parts, the weights would remain equal in each leg, and
therefore the fluid would rest in an equilibrium. But the centrifugal
force of every part is to the weight of the same part as 1 to 289; that
is, the centrifugal force, which should be 4/505
parts of the weight, is only 1/289
part thereof. And, therefore, I say, by the rule of proportion, that if
the centrifugal force 4/505
make the height of the water in the leg ACca to exceed the
height of the water in the leg QCcq by one 1/100
part of its whole height, the centrifugal force 1/289
will make the excess of the height in the leg ACca only
1/289 part of the height of
the water in the other leg QCcq; and therefore the diameter of
the earth at the equator, is to its diameter from pole to pole as 230 to
229. And since the mean semi-diameter of the
earth, according to Picart's mensuration, is 19615800 Paris
feet, or 3923,16 miles (reckoning 5000 feet to a mile), the earth will
be higher at the equator than at the poles by 85472 feet, or 171/10
miles. And its height at the equator will be about 19658600 feet, and at
the poles 19573000 feet.
If, the density and periodic time of the diurnal revolution remaining
the same, the planet was greater or less than the earth, the proportion
of the centrifugal force to that of gravity, and therefore also of the
diameter betwixt the poles to the diameter at the equator, would
likewise remain the same. But if the diurnal motion was accelerated or
retarded in any proportion, the centrifugal force would be augmented or
diminished nearly in the same duplicate proportion; and therefore the
difference of the diameters will be increased or diminished in the same
duplicate ratio very nearly. And if the density of the planet was
augmented or diminished in any proportion, the force of gravity tending
towards it would also be augmented or diminished in the same proportion:
and the difference of the diameters contrariwise would be diminished in
proportion as the force of gravity is augmented, and augmented in
proportion as the force of gravity is diminished. Wherefore, since the
earth, in respect of the fixed stars, revolves in 23h.56′,
but Jupiter in 9h.56′, and the squares of their periodic
times are as 29 to 5, and their densities as 400 to 94½, the difference
of the diameters of Jupiter will be to its lesser diameter as
29
5 x 400
941/2 x 1
229 to 1, or as 1 to 9⅓, nearly.
Therefore the diameter of Jupiter from east to west is to its diameter
from pole to pole nearly as 10⅓ to 9⅓. Therefore since its greatest
diameter is 37″, its lesser diameter lying between the poles will be 33″
25‴. Add thereto about 3″ for the irregular refraction of light, and the
apparent diameters of this planet will become 40″ and 36″ 25‴; which are
to each other as 111/6
to 101/6, very nearly.
These things are so upon the supposition that the body of Jupiter is
uniformly dense. But now if its body be denser towards the plane of the
equator than towards the poles, its diameters may be to each other as 12
to 11, or 13 to 12, or perhaps as 14 to 13.
And Cassini observed in the year 1691, that the diameter of
Jupiter reaching from east to west is greater by about a fifteenth part
than the other diameter. Mr. Pound with his 123 feet
telescope, and an excellent micrometer, measured the diameters of
Jupiter in the year 1719, and found them as follow.
| The Times. |
Greatest diam. |
Lesser diam. |
The diam. to each other. |
January
March
March
April
|
Day.
28
6
9
9
|
Hours
6
7
7
9
|
Parts
13,40
13,12
13,12
12,32
|
Parts
12,28
12,20
12,08
11,48
|
As
As
As
As
|
12
13¾
12⅔
14½
|
to
to
to
to
|
11
12¾
11⅔
13½
|
So that the theory agrees with the phaenomena;
for the planets are more heated by the sun's rays towards their
equators, and therefore are a little more condensed by that heat than
towards their poles.
Moreover, that there is a diminution of gravity occasioned by the
diurnal rotation of the earth, and therefore the earth rises higher
there than it does at the poles (supposing that its matter is uniformly
dense), will appear by the experiments of pendulums related under the
following Proposition.

Because the weights of the unequal legs of the canal of water ACQqca
are equal; and the weights of the parts proportional to the whole legs,
and alike situated in them, are one to another as the weights of the
wholes, and therefore equal betwixt themselves; the weights of equal
parts, and alike situated in the legs, will be reciprocally as the legs,
that is, reciprocally as 230 to 229. And the case is the same in all
homogeneous equal bodies alike situated in the legs of the canal. Their
weights are reciprocally as the legs, that is, reciprocally as the
distances of the bodies from the centre of the earth. Therefore if the
bodies are situated in the uppermost parts of the canals, or on the
surface of the earth, their weights will be one to another reciprocally
as their distances from the centre. And, by the same argument, the
weights in all other places round the whole surface of the earth are
reciprocally as the distances of the places from the centre; and,
therefore, in the hypothesis of the earth's being a spheroid are given
in proportion.
Whence arises this Theorem, that the increase of weight in passing from
the equator to the poles is nearly as the versed sine of double the
latitude; or, which comes to the same thing, as the square of the right
sine of the latitude; and the arcs of the degrees of latitude in the
meridian increase nearly in the same proportion. And, therefore, since
the latitude of Paris is 48° 50′, that of places under the
equator 00° 00′, and that of places under the poles 90°; and the versed
sines of double those arcs are 11334,00000 and 20000, the radius being
10000; and the force of gravity at the pole is to the force of gravity
at the equator as 230 to 229; and the excess of the force of gravity at
the pole to the force of gravity at the equator as 1 to 229; the excess
of the force of gravity in the latitude of Paris will be to the force of
gravity at the equator as 1 x 11334/20000
to 229, or as 5667 to 2290000. And therefore the whole forces of gravity
in those places will be one to the other as 2295667 to 2290000.
Wherefore since the lengths of pendulums vibrating in equal times are as
the forces of gravity, and in the latitude of Paris,
the length of a pendulum vibrating seconds is 3 Paris feet,
and 8½ lines, or rather because of the weight of the air, 85/9
lines, the length of a pendulum vibrating in the same time under the
equator will be shorter by 1,087 lines. And by a like calculus the
following table is made.
Latitude of
the place. |
Length of the
pendulum |
Measure of one degree
in the meridian. |
Deg.
0
5
10
15
20
25
30
35
40
1
2
3
4
45
6
7
8
9
50
55
60
65
70
75
80
85
90
|
Feet Lines
3 . 7,468
3 . 7,482
3 . 7,526
3 . 7,596
3 . 7,692
3 . 7,812
3 . 7,948
3 . 8,099
3 . 8,261
3 . 8,294
3 . 8,327
3 . 8,361
3 . 8,394
3 . 8,428
3 . 8,461
3 . 8,494
3 . 8,528
3 . 8,561
3 . 8,594
3 . 8,756
3 . 8,907
3 . 9,044
3 . 9,162
3 . 9,258
3 . 9,329
3 . 9,372
3 . 9,387
|
Toises.
56637
56642
56659
56687
56724
56769
56823
56882
56945
56958
56971
56984
56997
57010
57022
57035
57048
57061
57074
57137
57196
57250
57295
57332
57360
57377
57382
|
By this table, therefore, it appears that the inequality of degrees is
so small, that the figure of the earth, in geographical matters, may be
considered as spherical; especially if the earth be a little denser
towards the plane of the equator than towards the poles.
Now several astronomers, sent into remote countries to make
astronomical observations, have found that pendulum clocks do
accordingly move slower near the equator than in our climates. And,
first of all, in the year 1672, M. Richer took notice of it in
the island of Cayenne; for when, in the month of August,
he was observing the transits of the fixed stars over the meridian, he
found his clock to go slower than it ought in respect of the mean motion
of the sun at the rate of 2′ 28″ a day. Therefore, fitting up a simple
pendulum to vibrate in seconds, which were measured by an excellent
clock, he observed the length of that simple pendulum; and this he did
over and over every week for ten months together. And upon his re turn
to France, comparing the length of that pendulum with the
length of the pendulum at Paris
(which was 3 Paris feet and 83/5
lines), he found it shorter by 1¼ line.
Afterwards, our friend Dr. Halley, about the year 1677,
arriving at the island of St. Helena, found his pendulum clock
to go slower there than at London without marking the
difference. But he shortened the rod of his clock by more than the
1/8 of an inch, or 1½ line;
and to effect this, be cause the length of the screw at the lower end of
the rod was not sufficient, he interposed a wooden ring betwixt the nut
and the ball.
Then, in the year 1682, M. Varin and M. des Hayes
found the length of a simple pendulum vibrating in seconds at the Royal
Observatory of Paris to be 3 feet and 85/9
lines. And by the same method in the island of Goree, they
found the length of an isochronal pendulum to be 3 feet and 65/9
lines, differing from the former by two lines. And in the same year,
going to the islands of Guadaloupe and Martinico,
they found that the length of an isochronal pendulum in those islands
was 3 feet and 6½ lines.
After this, M. Couplet, the son, in the month of July
1697, at the Royal Observatory of Paris, so fitted his
pendulum clock to the mean motion of the sun, that for a considerable
time together the clock agreed with the motion of the sun. In November
following, upon his arrival at Lisbon, he found his clock to
go slower than before at the rate of 2′ 13″ in 24 hours. And next March
coming to Paraiba, he found his clock to go slower than at Paris,
and at the rate 4′ 12″ in 24 hours; and he affirms, that the pendulum
vibrating in seconds was shorter at Lisbon by 2½ lines, and at Paraiba,
by 3⅔ lines, than at Paris. He had done better to have
reckoned those differences 1⅓ and 25/9:
for these differences correspond to the differences of the times 2′ 13″
and 4′ 12″. But this gentleman's observations are so gross, that we
cannot confide in them.
In the following years, 1699, and 1700, M. des Hayes, making
another voyage to America, determined that in the island of Cayenne
and Granada the length of the pendulum vibrating in seconds
was a small matter less than 3 feet and 6½ lines; that in the island of
St. Christophers it was 3 feet and 6¾ lines; and in the island
of St. Domingo 3 feet and 7 lines.
And in the year 1704, P. Feuillé, at Puerto Bello
in America, found that the length of the pendulum vibrating in
seconds was 3 Paris feet, and only 57/12
lines, that is, almost 3 lines shorter than at Paris; but the
observation was faulty. For afterward, going to the island of Martinico,
he found the length of the isochronal pendulum there 3 Paris
feet and 510/12 lines.
Now the latitude of Paraiba is 6° 38′ south; that of Puerto
Bello 9° 33′ north; and the latitudes of the islands Cayenne,
Goree, Gaudaloupe, Martinico, Granada, St. Christophers, and St.
Domingo, are respectively 4° 55′, 14° 40″, 15° 00′, 14° 44′, 12°
06′, 17° 19′, and 19° 48′, north. And the
excesses of the length of the pendulum at Paris above the
lengths of the isochronal pendulums observed in those latitudes are a
little greater than by the table of the lengths of the pendulum before
computed. And therefore the earth is a little higher under the equator
than by the preceding calculus, and a little denser at the centre than
in mines near the su face, unless, perhaps, the heats of the torrid zone
have a little extended the length of the pendulums.
For M. Picart has observed, that a rod of iron, which in
frosty weather in the winter season was one foot long, when heated by
fire, was lengthened into one foot and ¼ line. Afterward M. de la
Hire found that a rod of iron, which in the like winter season
was 6 feet long, when exposed to the heat of the summer sun, was
extended into 6 feet and ⅔ line. In the former case the heat was greater
than in the latter; but in the latter it was greater than the heat of
the external parts of a human body; for metals exposed to the summer sun
acquire a very considerable degree of heat. But the rod of a pendulum
clock is never exposed to the heat of the summer sun, nor ever acquires
a heat equal to that of the external parts of a human body; and,
therefore, though the 3 feet rod of a pendulum clock will indeed be a
little longer in the summer than in the winter season, yet the
difference will scarcely amount to ¼ line. Therefore the total
difference of the lengths of isochronal pendulums in different climates
cannot be ascribed to the difference of heat; nor indeed to the mistakes
of the French astronomers. For although there is not a perfect
agreement betwixt their observations, yet the errors are so small that
they may be neglected; and in this they all agree, that isochronal
pendulums are shorter under the equator than at the Royal Observatory of
Paris, by a difference not less than 1¼ line, nor greater than
2⅔ lines. By the observations of M. Richer, in the island of Cayenne,
the difference was 1¼ line. That difference being corrected by those of
M. des Hayes, becomes 1½ line or 1¾ line. By the less accurate
observations of others, the same was made about two lines. And this dis
agreement might arise partly from the errors of the observations, partly
from the dissimilitude of the internal parts of the earth, and the
height of mountains; partly from the different heats of the air.
I take an iron rod of 3 feet long to be shorter by a sixth part of one
line in winter time with us here in England than in the
summer. Because of the great heats under the equator, subduct this
quantity from the difference of one line and a quarter observed by M. Richer,
and there will remain one line 1/12,
which agrees very well with 187/1000
line collected, by the theory a little before. M. Richer
repeated his observations, made in the island of Cayenne,
every week for ten months together, and compared the lengths of the
pendulum which he had there noted in the iron rods with the lengths
thereof which he observed in France. This diligence and care
seems to have been wanting to the other observers. If this gentleman's
observations are to be depended on, the earth
is higher under the equator than at the poles, and that by an excess of
about 17 miles; as appeared above by the theory.
The proposition appears from Cor. 20, Prop. LXVI, Book I; but that
motion of nutation must be very small, and, indeed, scarcely
perceptible.
That the greater planets, while they are carried about the sun, may in
the mean time carry other lesser planets, revolving about them; and that
those lesser planets must move in ellipses which have their foci in the
centres of the greater, appears from Prop. LXV, Book I. But then their
motions will be several ways disturbed by the action of the sun, and
they will suffer such inequalities as are observed in our moon. Thus our
moon (by Cor. 2, 3, 4, and 5, Prop. LXVI, Book I) moves faster, and, by
a radius drawn to the earth, describes an area greater for the time, and
has its orbit less curved, and therefore approaches nearer to the earth
in the syzygies than in the quadratures, excepting in so far as these
effects are hindered by the motion of eccentricity; for (by Cor. 9,
Prop. LXVI, Book I) the eccentricity is greatest when the apogeon of the
moon is in the syzygies, and least when the same is in the quadratures;
and upon this account the perigeon moon is swifter, and nearer to us,
but the apogeon moon slower, and farther from us, in the syzygies than
in the quadratures. Moreover, the apogee goes forward, and the nodes
backward; and this is done not with a regular but an unequal motion. For
(by Cor. 7 and 8, Prop. LXVI, Book I) the apogee goes more swiftly
forward in its syzygies, more slowly backward in its quadratures; and,
by the excess of its progress above its regress, advances yearly in
consequentia. But, contrariwise, the nodes (by Cor. 11, Prop.
LXVI, Book I) are quiescent in their syzygies, and go fastest back in
their quadratures. Farther, the greatest latitude of the moon (by Cor.
10, Prop. LXVI, Book I) is greater in the quadratures of the moon than
in its syzygies. And (by Cor. 6, Prop. LXVI, Book I) the mean motion of
the moon is slower in the perihelion of the earth than in its aphelion.
And these are the principal inequalities (of the moon) taken notice of
by astronomers.
But there are yet other inequalities not
observed by former astronomers, by which the motions of the moon are so
disturbed, that to this day we have not been able to bring them under
any certain rule. For the velocities or horary motions of the apogee and
nodes of the moon, and their equations, as well as the difference
betwixt the greatest eccentricity in the syzygies, and the least
eccentricity in the quadratures, and that inequality which we call the
variation, are (by Cor. 14, Prop. LXVI, Book I) in the course of the
year augmented and diminished in the triplicate proportion of the sun's
apparent diameter. And besides (by Cor. 1 and 2, Lem. 10, and Cor. 16,
Prop. LXVI, Book I) the variation is augmented and diminished nearly in
the duplicate proportion of the time between the quadratures. But in
astronomical calculations, this inequality is commonly thrown into and
confounded with the equation of the moon's centre.
From the motions of our moon we deduce the corresponding motions of the
moons or satellites of Jupiter in this manner, by Cor. 16, Prop. LXVI,
Book I. The mean motion of the nodes of the outmost satellite of Jupiter
is to the mean motion of the nodes of our moon in a proportion
compounded of the duplicate proportion of the periodic times of the
earth about the sun to the periodic times of Jupiter about the sun, and
the simple proportion of the periodic time of the satellite about
Jupiter to the periodic time of our moon about the earth; and,
therefore, those nodes, in the space of a hundred years, are carried 8°
24′ backward, or in antecedentia. The mean motions of the
nodes of the inner satellites are to the mean motion of the nodes of the
outmost as their periodic times to the periodic time of the former, by
the same Corollary, and are thence given. And the motion of the apsis of
every satellite in consequentia is to the motion of its nodes
in antecedentia as the motion of the apogee of our moon to the
motion of its nodes (by the same Corollary), and is thence given. But
the motions of the apsides thus found must be diminished in the
proportion of 5 to 9, or of about 1 to 2, on account of a cause which I
cannot here descend to explain. The greatest equations of the nodes, and
of the apsis of every satellite, are to the greatest equations of the
nodes, and apogee of our moon respectively, as the motions of the nodes
and apsides of the satellites, in the time of one revolution of the
former equations, to the motions of the nodes and apogee of our moon, in
the time of one revolution of the latter equations. The variation of a
satellite seen from Jupiter is to the variation of our moon in the same
proportion as the whole motions of their nodes respectively
during the times in which the satellite and our moon (after parting
from) are revolved (again) to the sun, by the same Corollary; and
therefore in the outmost satellite the variation does not exceed 5″ 12‴.
By Cor. 19 and 20, Prop. LXVI, Book I, it appears that the waters of
the sea ought twice to rise and twice to fall every day, as well lunar
as solar; and that the greatest height of the waters in the open and
deep seas ought to follow the appulse of the luminaries to the meridian
of the place by a less interval than 6 hours; as happens in all that
eastern tract of the Atlantic and AEthiopic seas between France
and the Cape of Good Hope; and on the coasts of Chili
and Peru, in the South Sea; in all which shores the
flood falls out about the second, third, or fourth hour, unless where
the motion propagated from the deep ocean is by the shallowness of the
channels, through which it passes to some particular places, retarded to
the fifth, sixth, or seventh hour, and even later. The hours I reckon
from the appulse of each luminary to the meridian of the place; as well
under as above the horizon; and by the hours of the lunar day I
understand the 24th parts of that time which the moon, by its apparent
diurnal motion, employs to come about again to the meridian of the place
which it left the day before. The force of the sun or moon in raising
the sea is greatest in the appulse of the luminary to the meridian of
the place; but the force impressed upon the sea at that time continues a
little while after the impression, and is afterwards increased by a new
though less force still acting upon it. This makes the sea rise higher
and higher, till this new force becoming too weak to raise it any more,
the sea rises to its greatest height. And this will come to pass,
perhaps, in one or two hours, but more frequently near the shores in
about three hours, or even more, where the sea is shallow.
The two luminaries excite two motions, which will not appear
distinctly, but between them will arise one mixed motion compounded out
of both. In the conjunction or opposition of the luminaries their forces
will be conjoined, and bring on the greatest flood and ebb. In the
quadratures the sun will raise the waters which the moon depresses, and
depress the waters which the moon raises, and from the difference of
their forces the smallest of all tides will follow. And because (as
experience tells us) the force of the moon is greater than that of the
sun, the greatest height of the waters will happen about the third lunar
hour. Out of the syzygies and quadratures, the greatest tide, which by
the single force of the moon ought to fall out at the third lunar hour,
and by the single force of the sun at the third solar hour, by the
compounded forces of both must fall out in an intermediate time
that aproaches nearer to the third hour of the moon than to that of the
sun. And, therefore, while the moon is passing from the syzygies to the
quadratures, during which time the 3d hour of the sun precedes the 3d
hour of the moon, the greatest height of the waters will also precede
the 3d hour of the moon, and that, by the greatest interval, a little
after the octants of the moon; and, by like intervals, the greatest tide
will fol low the 3d lunar hour, while the moon is passing from the
quadratures to the syzygies. Thus it happens in the open sea; for in the
mouths of rivers the greater tides come later to their height.
But the effects of the luminaries depend upon their distances from the
earth; for when they are less distant, their effects are greater, and
when more distant, their effects are less, and that in the triplicate
proportion of their apparent diameter. Therefore it is that the sun, in
the winter time, being then in its perigee, has a greater effect, and
makes the tides in the syzygies something greater, and those in the
quadratures something less than in the summer season; and every month
the moon, while in the perigee, raises greater tides than at the
distance of 15 days before or after, when it is in its apogee. Whence it
comes to pass that two highest tides do not follow one the other in two
immediately succeeding syzygies.
The effect of either luminary doth likewise depend upon its declination
or distance from the equator; for if the luminary was placed at the
pole, it would constantly attract all the parts of the waters without
any intension or remission of its action, and could cause no
reciprocation of motion. And, therefore, as the luminaries decline from
the equator towards either pole, they will, by degrees, lose their
force, and on this account will excite lesser tides in the solstitial
than in the equinoctial syzygies. But in the solstitial quadratures they
will raise greater tides than in the quadratures about the equinoxes;
because the force of the moon, then situated in the equator, most
exceeds the force of the sun. Therefore the greatest tides fall out in
those syzygies, and the least in those quadratures, which happen about
the time of both equinoxes: and the greatest tide in the syzygies is
always succeeded by the least tide in the quadratures, as we find by
experience. But, because the sun is less distant from the earth in
winter than in summer, it comes to pass that the greatest and least
tides more frequently appear before than after the vernal equinox, and
more frequently after than before the autumnal.
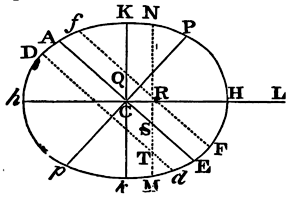
Moreover, the effects of the luminaries depend upon the latitudes of
places. Let ApEP represent the earth covered with deep waters;
C its centre; P, p its poles; AE the equator; F any place
without the equator; Ff the parallel of the place; Dd
the correspondent parallel on the other side of
the equator; L the place of the moon three Hours before; H the place of
the earth directly under it; h the opposite place; K, k
the places at 90 degrees distance; CH, Ch, the greatest heights
of the sea from the centre of the earth; and CK, Ck, its least
heights: and if with the axes Hh, Kk, an ellipsis is
described, and by the revolution of that ellipsis about its longer axis
Hh a spheroid HPKhpk is formed, this spheroid will
nearly represent the figure of the sea; and CF, Cf, CD, Cd,
will represent the heights of the sea in the places Ff, Dd.
But farther; in the said revolution of the ellipsis any point N
describes the circle NM cutting the parallels Ff, Dd,
in any places RT, and the equator AE in S; CN will represent the height
of the sea in all those places R, S, T, situated in this circle.
Wherefore, in the diurnal revolution of any place F, the greatest flood
will be in F, at the third hour after the appulse of the moon to the
meridian above the horizon; and afterwards the greatest ebb in Q, at the
third hour after the setting of the moon; and then the greatest flood in
f, at the third hour after the appulse of the moon to the
meridian under the horizon; and, lastly, the greatest ebb in Q, at the
third hour after the rising of the moon; and the latter flood in f will
be less than the preceding flood in F. For the whole sea is divided into
two hemispherical floods, one in the hemisphere KHk on the
north side, the other in the opposite hemisphere Khk, which we
may therefore call the northern and the southern floods. These floods,
being always opposite the one to the other, come by turns to the
meridians of all places, after an interval of 12 lunar hours. And seeing
the northern countries partake more of the northern flood, and the
southern countries more of the southern flood, thence arise tides,
alternately greater and less in all places without the equator, in which
the luminaries rise and set. But the greatest tide will happen when the
moon declines towards the vertex of the place, about the third hour
after the appulse of the moon to the meridian above the horizon; and
when the moon changes its declination to the other side of the
equator, that which was the greater tide will be changed into a
lesser. And the greatest difference of the floods will fall out about
the times of the solstices; especially if the ascending node of the moon
is about the first of Aries. So it is found by experience that the
morning tides in winter exceed those of the evening, and the evening
tides in summer exceed those of the morning; at Plymouth by
the height of one foot, but at Bristol by the height of 15
inches, according to the observations of Colepress and Sturmy.
But the motions which we have been describing suffer some alteration
from that force of reciprocation, which the waters, being once moved,
retain a little while by their vis insita. Whence it comes to
pass that the tides may continue for some time, though the actions of
the luminaries should cease. This power of
retaining the impressed motion lessens the difference of the alternate
tides, and makes those tides which immediately succeed after the
syzygies greater, and those which follow next after the quadratures
less. And hence it is that the alternate tides at Plymouth and
Bristol do not differ much more one from the other than by the
height of a foot or 15 inches, and that the greatest tides of all at
those ports are not the first but the third after the syzygies. And,
besides, all the motions are retarded in their passage through shallow
channels, so that the greatest tides of all, in some straits and mouths
of rivers, are the fourth or even the fifth after the syzygies.
Farther, it may happen that the tide may be propagated from the ocean
through different channels towards the same port, and may pass quicker
through some channels than through others; in which case the same tide,
divided into two or more succeeding one another, may compound new
motions of different kinds. Let us suppose two equal tides flowing
towards the same port from different places, the one preceding the other
by 6 hours; and suppose the first tide to happen at the third hour of
the appulse of the moon to the meridian of the port. If the moon at the
time of the appulse to the meridian was in the equator, every 6 hours
alternately there would arise equal floods, which, meeting with as many
equal ebbs, would so balance one the other, that for that day, the water
would stagnate and remain quiet. If the moon then declined from the
equator, the tides in the ocean would be alternately greater and less,
as was said; and from thence two greater and two lesser tides would be
alternately propagated towards that port. But the two greater floods
would make the greatest height of the waters to fall out in the middle
time betwixt both; and the greater and lesser floods would make the
waters to rise to a mean height in the middle time between them, and in
the middle time between the two lesser floods the waters would rise to
their least height. Thus in the space of 24 hours the waters would come,
not twice, as commonly, but once only to their great est, and once only
to their least height; and their greatest height, if the moon declined
towards the elevated pole, would happen at the 6th or 30th hour after
the appulse of the moon to the meridian; and when the moon changed its
declination, this flood would be changed into an ebb. An example of all
which Dr. Halley has given us, from the observations of sea
men in the port of Batsham, in the kingdom of Tunquin,
in the latitude of 20° 50′ north. In that port, on the day which follows
after the passage of the moon over the equator, the waters stagnate:
when the moon declines to the north, they begin to flow and ebb, not
twice, as in other ports, but once only every day: and the flood happens
at the setting, and the greatest ebb at the rising of the moon. This
tide increases with the declination of the moon till the 7th or 8th day;
then for the 7 or 8 days following it decreases
at the same rate as it had increased before, and ceases when the moon
changes its declination, crossing over the equator to the south. After
which the flood is immediately changed into an ebb; and thenceforth the
ebb happens at the setting and the flood at the rising of the moon; till
the moon, again passing the equator, changes its declination. There are
two inlets to this port and the neighboring channels, one from the seas
of China, between the continent and the island of Leuconia;
the other from the Indian sea, between the continent and the
island of Borneo. But whether there be really two tides
propagated through the said channels, one from the Indian sea
in the space of 12 hours, and one from the sea of China in the
space of 6 hours, which therefore happening at the 3d and 9th lunar
hours, by being compounded together, produce those motions; or whether
there be any other circumstances in the state of those seas. I leave to
be determined by observations on the neighbouring shores.
Thus I have explained the causes of the motions of the moon and of the
sea. Now it is fit to subjoin something concerning the quantity of those
motions.
Let S represent the sun, T the earth, P the moon, CADB the moon's
orbit. In SP take SK equal to ST; and let SL be to SK in the duplicate
proportion of SK to SP: draw LM parallel to PT; and if ST or SK is
supposed to represent the accelerated force of gravity of the earth
towards the sun, SL will represent the accelerative force of gravity of
the moon towards the sun. But that force is compounded of the parts SM
and LM, of which the force LM, and that part of SM which is represented
by TM, disturb the motion of the moon, as we have shewn in Prop. LXVI,
Book I, and its Corollaries. Forasmuch as the earth and moon are
revolved about their common centre of gravity, the motion of the earth
about that centre will be also disturbed by the like forces; but we may
consider the sums both of the forces and of the motions as in the moon,
and represent the sum of the forces by the lines TM and ML, which are
analogous to thorn both. The force ML (in its mean quantity) is to the
centripetal force by which the moon may be retained in its orbit
revolving about the earth at rest, at the distance PT, in the duplicate
proportion of the periodic time of the moon about the earth to the
periodic time of the earth about the sun (by Cor. 17, Prop. LXVI, Book
I); that is, in the duplicate proportion of 27d.7h.43′
to 365d.6h.9′; or as 1000 to 178725; or as 1 to
17829/40. But in the
4th Prop. of this Book we found, that, if both earth
and moon were revolved about their common centre of gravity, the mean
distance of the one from the other would be nearly 60½ mean
semi-diameters of the earth; and the force by which the moon may be kept
revolving in its orbit about the earth in rest at the distance PT of 60½
semi-diameters of the earth, is to the force by which it may be revolved
in the same time, at the distance of 60 semi-diameters, as 60½ to 60:
and this force is to the force of gravity with us very nearly as 1 to 60
x 60. Therefore the mean force ML is to the force of gravity on the
surface of our earth as 1 x 60½ to 60 x 60 x 60 x 17829/40,
or as 1 to 638092,6; whence by the proportion of the lines TM, ML, the
force TM is also given; and these are the forces with which the sun
disturbs the motions of the moon. Q.E.I.
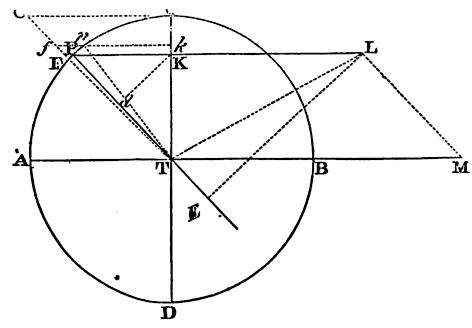
We have above shown that the area which the moon describes by a radius
drawn to the earth is proportional to the time of description, excepting
in so far as the moon's motion is disturbed by the action of the sun;
and here we propose to investigate the inequality of the moment, or
horary increment of that area or motion so disturbed. To
render the calculus more easy, we shall suppose the orbit of the moon to
be circular, and neglect all inequalities but that only which is now
under consideration; and, because of the immense distance of the sun, we
shall farther suppose that the lines SP and ST are parallel. By this
means, the force LM will be always reduced to its mean quantity TP, as
well as the force TM to its mean quantity 3PK. These forces (by Cor. 2
of the Laws of Motion) compose the force TL; and this force, by letting
fall the perpendicular LE upon the radius TP, is resolved into the
forces TE, EL; of which the force TE, acting constantly in the direction
of the radius TP, neither accelerates nor retards the description of the
area TPC made by that radius TP; but EL, acting on the radius
TP in a perpendicular direction, accelerates or retards the
description of the area in proportion as it accelerates or
retards the moon. That acceleration of the
moon, in its passage from the quadrature C to the conjunction A, is in
every moment of time as the generating accelerative force EL,
that is, as 3PK x TK
TP. Let the time be represented by the
mean motion of the moon, or (which comes to the same thing) by the angle
CTP, or even by the arc CP. At right angles upon CT erect CG equal to
CT; and, supposing the quadrantal arc AC to be divided into an infinite
number of equal parts Pp, &c., these parts may
represent the like infinite number of the equal parts of time.
Let fall pk perpendicular on CT, and draw TG meeting with KP,
kp produced in F and f; then will FK be equal to TK,
and Kk be to PK as Pp to Tp, that is, in a
given proportion; and therefore FK x Kk, or the area FKkf,
will be as 3PK x TK
TP, that is, as EL; and compounding, the
whole area GCKF will be as the sum of all the forces EL impressed upon
the moon in the whole time CP; and therefore also as the velocity
generated by that sum, that is, as the acceleration of the description
of the area CTP, or as the increment of the moment thereof.
The force by which the moon may in its periodic time CADB of 27d.7h.43′
be retained revolving about the earth in rest at the distance TP, would
cause a body falling in the time CT to describe the length ½CT, and at
the same time to acquire a velocity equal to that with which the moon is
moved in its orbit. This appears from Cor. 9, Prop, IV., Book I. But
since Kd, drawn perpendicular on TP, is but a third
part of EL, and equal to the half of TP, or ML, in the
octants, the force EL in the octants, where it is greatest, will exceed
the force ML in the proportion of 3 to 2; and therefore will be to that
force by which the moon in its periodic time may be retained revolving
about the earth at rest as 100 to ⅔ x 178721½, or 11915; and in the time
CT will generate a velocity equal to 100/11915
parts of the velocity of the moon; but in the time CPA will generate a
greater velocity in the proportion of CA to CT or TP. Let the greatest
force EL in the octants be represented by the area FK x Kk, or
by the rectangle ½TP x Pp, which is equal thereto; and the
velocity which that greatest force can generate in any time CP will be
to the velocity which any other lesser force EL can generate in the same
time as the rectangle ½TP x CP to the area KCGF; but the velocities
generated in the whole time CPA will be one to the other as the
rectangle ½TP x CA to the triangle TCG, or as the quadrantal arc CA to
the radius TP; and therefore the latter velocity generated in the whole
time will be 100/11915
parts of the velocity of the moon. To this velocity of the moon, which
is proportional to the mean moment of the area (supposing this mean
moment to be represented by the number 11915), we add and subtract the
half of the other velocity; the sum 11915 + 50, or 11965, will represent
the greatest moment of the area in the syzygy A; and the difference
11915 − 50, or 11865, the least moment thereof in the quadratures.
Therefore the areas which in equal times are described in the syzygies
and quadratures are one to the other as 11965 to 11865. And if to the
least moment 11865 we add a moment which shall be to 100, the difference
of the two former moments, as the trapezium FKCG to the triangle TCG,
or, which comes to the same thing, as the square of the sine PK to the
square of the radius TP (that is, as Pd to TP), the sum will
represent the moment of the area when the moon is in any intermediate
place P.
But these things take place only in the hypothesis that the sun and the
earth are at rest, and that the synodical revolution of the moon is
finished in 27d.7h.43′. But since the moon's
synodical period is really 29d.12h.41′, the
increments of the moments must be enlarged in the same proportion as the
time is, that is, in the proportion of 1080853 to 1000000. Upon which
account, the whole increment, which was 100/11915
parts of the mean moment, will now become T100/11023
parts thereof; and therefore the moment of the area in the quadrature of
the moon will be to the moment thereof in the syzygy as 11023 − 50 to
11023 + 50; or as 10973 to 11073: and to the moment thereof, when the
moon is in any intermediate place P, as 10973 to 10973 + Pd;
that is, supposing TP = 100.
The area, therefore, which the moon, by a radius drawn to the earth,
describes in the several little equal parts of time, is nearly as the
sum of the number 219,46, and the versed sine of the double distance of
the moon from the nearest quadrature, considered in a circle which hath
unity for its radius. Thus it is when the variation in the octants is in
its mean quantity. But if the variation there is greater or less, that
versed sine must be augmented or diminished in the same proportion.
The area which the moon, by a radius drawn to the earth, describes in
every, moment of time, is as the horary motion of the moon and the
square of the distance of the moon from the earth conjunctly. And
therefore the distance of the moon from the earth is in a proportion
compounded of the subduplicate proportion of the area directly, and the
subduplicate proportion of the horary motion inversely.
Q.E.I.
Cor. 1. Hence the apparent diameter of the moon
is given; for it is reciprocally as the distance of the moon from the
earth. Let astronomers try how accurately this rule agrees with the
phaenomena.
Cor. 2. Hence also the orbit of the moon may be
more exactly defined from the phaenomena than hitherto could be done.
The curvature of the orbit which a body describes, if attracted in
lines perpendicular to the orbit, is as the force of attraction
directly, and the square of the velocity inversely. I estimate the
curvatures of lines compared one with another according to the
evanescent proportion of the sines or tangents of their angles of
contact to equal radii, supposing those radii to be infinitely
diminished. But the attraction of the moon towards the earth in the
syzygies is the excess of its gravity towards the earth above the force
of the sun 2PK (see Fig. Prop. XXV), by which force the accelerative
gravity of the moon towards the sun exceeds the accelerative gravity of
the earth towards the sun, or is exceeded by it. But in the quadratures
that attraction is the sum of the gravity of the moon towards the earth,
and the sun's force KT, by which the moon is attracted towards the
earth. And these attractions, putting N for AT+CT
2, are nearly as
178725
AT2-2000
CT x N and 178725
CT2+1000
AT x N, or as 178725N x CT² − 2000AT² x
CT, and 178725N x AT² + 1000CT² x AT. For if the accelerative gravity of
the moon towards the earth be represented by the number 178725, the mean
force ML, which in the quadratures is PT or TK, and draws the moon
towards the earth, will be 1000, and the mean force TM in the syzygies
will be 3000; from which, if we subtract the mean force ML, there will
remain 2000, the force by which the moon in the syzygies is drawn from
the earth, and which we above called 2PK. But the velocity of the moon
in the syzygies A and B is to its velocity in the quadratures C and D as
CT to AT, and the moment of the area, which the moon by a radius drawn
to the earth describes in the syzygies, to the moment of that area described
in the quadratures conjunctly; that is, as 11073CT to 10973AT. Take this
ratio twice inversely, and the former ratio once directly, and the
curvature of the orb of the moon in the syzygies will be to the
curvature thereof in the quadratures as 120406729 x 178725AT² x CT² x N
− 120406729 x 2000AT4 x CT to 122611329 x 178725AT² x CT² x N
+ 122611329 x 1000CT4 x AT, that is, as 2151969AT x CT x N −
24081AT³ to 2191371AT x CT x N + 12261CT³.
Because the figure of the moon's orbit is unknown, let us, in its
stead, assume the ellipsis DBCA, in the centre of which we suppose the
earth to be situated, and the greater axis DC to lie between the
quadratures as the lesser AB between the syzygies. But since the plane
of this ellipsis is revolved about the earth by an angular motion, and
the orbit, whose curvature we now examine, should be described in a
plane void of such motion
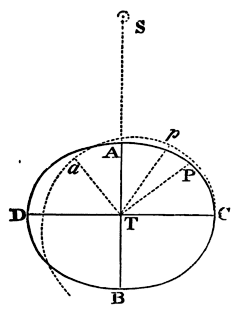 we are to consider the figure which the moon, while it is revolved in
that ellipsis, describes in this plane, that is to say, the figure Cpa,
the several points p of which are found by assuming any point
P in the ellipsis, which may represent the place of the moon, and
drawing Tp equal to TP in such manner that the angle PTp
may be equal to the apparent motion of the sun from the time of the last
quadrature in C; or (which comes to the same thing) that the angle CTp
may be to the angle CTP as the time of the synodic revolution of the
moon to the time of the periodic revolution thereof, or as 29d.12h.44′
to 27d.7h.43′. If, therefore, in this proportion
we take the angle CTa to the right angle CTA, and make Ta
of equal length with TA, we shall have a the lower and C the
upper apsis of this orbit Cpa. But, by computation, I find that
the difference betwixt the curvature of this orbit Cpa at the
vertex a, and the curvature of a circle described about the
centre T with the interval TA, is to the difference between the
curvature of the ellipsis at the vertex A, and the curvature of the same
circle, in the duplicate proportion of the angle CTP to the angle CTp;
and that the curvature of the ellipsis in A is to the curvature of that
circle in the duplicate proportion of TA to TC; and the curvature of
that circle to the curvature of a circle described about the centre T
with the interval TC as TC to TA; but that the curvature of this last
arch is to the curvature of the ellipsis in C in the duplicate
proportion of TA to TC; and that the difference betwixt the curvature of
the ellipsis in the vertex C, and the curvature of this last circle, is
to the difference betwixt the curvature of the figure Cpa, at
the vertex C, and the curvature of this same last circle, in
the duplicate proportion of the angle CTp to the angle CTP; all
which proportions are easily drawn from the sines of the angles of
contact, and of the differences of those angles. But, by comparing those
proportions together, we find the curvature of the figure Cpa
at a to be to its curvature at C as AT³ − 16824/100000CT²
AT to CT³ + 16824/100000AT²
x CT; where the number 16824/100000
represents the difference of the squares of the angles CTP and CTp,
applied to the square of the lesser angle CTP; or (which is all one) the
difference of the squares of the times 27d.7h.43′,
and 29d.12j.44′, applied to the square of the time
27d.7h.43′, and 27d.7h.43′
we are to consider the figure which the moon, while it is revolved in
that ellipsis, describes in this plane, that is to say, the figure Cpa,
the several points p of which are found by assuming any point
P in the ellipsis, which may represent the place of the moon, and
drawing Tp equal to TP in such manner that the angle PTp
may be equal to the apparent motion of the sun from the time of the last
quadrature in C; or (which comes to the same thing) that the angle CTp
may be to the angle CTP as the time of the synodic revolution of the
moon to the time of the periodic revolution thereof, or as 29d.12h.44′
to 27d.7h.43′. If, therefore, in this proportion
we take the angle CTa to the right angle CTA, and make Ta
of equal length with TA, we shall have a the lower and C the
upper apsis of this orbit Cpa. But, by computation, I find that
the difference betwixt the curvature of this orbit Cpa at the
vertex a, and the curvature of a circle described about the
centre T with the interval TA, is to the difference between the
curvature of the ellipsis at the vertex A, and the curvature of the same
circle, in the duplicate proportion of the angle CTP to the angle CTp;
and that the curvature of the ellipsis in A is to the curvature of that
circle in the duplicate proportion of TA to TC; and the curvature of
that circle to the curvature of a circle described about the centre T
with the interval TC as TC to TA; but that the curvature of this last
arch is to the curvature of the ellipsis in C in the duplicate
proportion of TA to TC; and that the difference betwixt the curvature of
the ellipsis in the vertex C, and the curvature of this last circle, is
to the difference betwixt the curvature of the figure Cpa, at
the vertex C, and the curvature of this same last circle, in
the duplicate proportion of the angle CTp to the angle CTP; all
which proportions are easily drawn from the sines of the angles of
contact, and of the differences of those angles. But, by comparing those
proportions together, we find the curvature of the figure Cpa
at a to be to its curvature at C as AT³ − 16824/100000CT²
AT to CT³ + 16824/100000AT²
x CT; where the number 16824/100000
represents the difference of the squares of the angles CTP and CTp,
applied to the square of the lesser angle CTP; or (which is all one) the
difference of the squares of the times 27d.7h.43′,
and 29d.12j.44′, applied to the square of the time
27d.7h.43′, and 27d.7h.43′
Since, therefore, a represents the syzygy of the moon, and C
its quadrature, the proportion now found must be the same with that
proportion of the curvature of the moon's orb in the syzygies to the
curvature thereof in the quadratures, which we found above. Therefore,
in order to find the proportion of CT to AT,
let us multiply the extremes and the means, and the terms which come
out, applied to AT x CT, become 2062,79CT4 - 2151969N x CT³ +
368676N x AT x CT² + 36342AT² x CT² − 362047N x AT² x CT + 2191371N x
AT³ + 4051,4AT4 = 0. Now if for the half sum N of the terms
AT and CT we put 1, and x for their half difference, then CT
will be = 1 + x, and AT = 1 − x. And substituting
those values in the equation, after resolving thereof, we shall find x
= 0,00719; and from thence the semi-diameter CT = 1,00719, and the
semi-diameter AT = 0,99281, which numbers are nearly as 701/24,
and 691/24. Therefore
the moon's distance from the earth in the syzygies is to its distance in
the quadratures (setting aside the consideration of eccentricity) as 69
1/24 to 701/24;
or, in round numbers, as 69 to 70.
This inequality is owing partly to the elliptic figure of the moon's
orbit, partly to the inequality of the moments of the area which the
moon by a radius drawn to the earth describes. If the moon P revolved in
the ellipsis DBCA about the earth quiescent in the centre of the
ellipsis, and by the radius TP, drawn to the earth, described the area
CTP, proportional to the time of description; and the greatest
semi-diameter CT of the ellipsis was to the least TA as 70 to 69; the
tangent of the angle CTP would be to the tangent of the angle of the
mean motion, computed from the quadrature C, as the semi-diameter TA of
the ellipsis to its semi-diameter TC, or as 69 to 70. But the
description of the area CTP, as the moon advances from the quadrature to
the syzygy, ought to be in such manner accelerated, that the moment of
the area in the moon's syzygy may be to the moment thereof in its
quadrature as 11073 to 10973; and that the excess of the moment in any
intermediate place P above the moment in the quadrature may be as the
square of the sine of the angle CTP; which we may effect with accuracy
enough, if we diminish the tangent of the angle CTP in the subduplicate
proportion of the number 10973 to the number 11073, that is, in
proportion of the number 68,6877 to the number 69. Upon which account
the tangent of the angle CTP will now be to the tangent of the mean
motion as 68,6877 to 70; and the angle CTP in the octants, where the
mean motion is 45°, will be found 44°27′28″, which subtracted from 45°,
the angle of the mean motion, leaves the greatest variation 32′32″. Thus
it would be, if the moon, in passing from the quadrature to the syzygy,
described an angle CTA of 90 degrees only. But because of the motion of
the earth, by which the sun is apparently transferred in
consequentia, the moon, before it overtakes the sun, describes an
angle CT, greater than a right angle, in the proportion of the time of
the synodic revolution of the moon to the time of its periodic
revolution, that is, in the proportion of 29d.12h.44′
to 27d.7h.43′. Whence it comes to pass that all
the angles about the centre T are dilated in the same proportion; and
the greatest variation, which otherwise would be but 32′ 32″,
now augmented in the said proportion, becomes 35′ 10″.
And this is its magnitude in the mean distance of the sun from the
earth, neglecting the differences which may arise from the curvature of
the orbis magnus, and the stronger action of the sun upon the
moon when horned and new, than when gibbous and full. In other distances
of the sun from the earth, the greatest variation is in a proportion
compounded of the duplicate proportion of the time of the synodic
revolution of the moon (the time of the year being given) directly, and
the triplicate proportion of the distance of the sun from the earth
inversely. And, therefore, in the apogee of the sun, the greatest
variation is 33′14″, and in its perigee 37′11″, if the eccentricity of
the sun is to the transverse semi-diameter of the orbis magnus
as 1615/16 to 1000.
Hitherto we have investigated the variation in an orb not eccentric, in
which, to wit, the moon in its octants is always in its mean distance
from the earth. If the moon, on account of its eccentricity, is more or
less removed from the earth than if placed in this orb, the variation
may be something greater, or something less, than according to this
rule. But I leave the excess or defect to the determination of
astronomers from the phenomena.
Let S represent the sun, T the earth, P the moon, NPn the
orbit of the moon, Npn the orthographic projection of the orbit
upon the plane of the ecliptic: N, n the nodes, nTNm
the line of the nodes produced indefinitely;
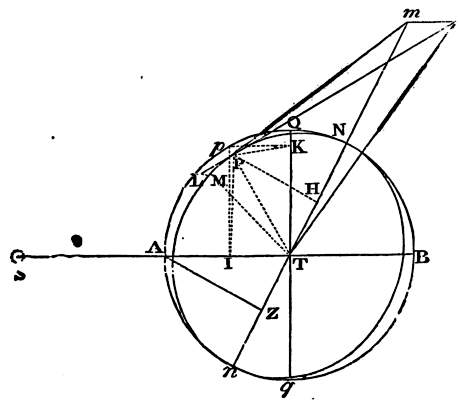 PI, PK perpendiculars upon the lines ST, Qq;
Pp a perpendicular upon the plane of the ecliptic; A, B the
moon's syzygies in the plane of the ecliptic; AZ a perpendicular let
fall upon Nn, the line of the nodes; Q, g the
quadratures of the moon in the plane of the ecliptic, and pK a
perpendicular on the line Qq lying between the quadratures. The
force of the sun to disturb the motion of the moon (by Prop. XXV) is
twofold, one proportional to the line LM, the other to the line MT, in
the scheme of that Proposition; and the moon by the former force is
drawn towards the earth, by the latter towards the sun, in a direction
parallel to the right line ST joining the earth and the sun. The former
force LM acts in the direction of the plane of the moon's orbit, and
therefore makes no change upon the situation thereof, and is upon that
account to be neglected; the latter force MT, by which the plane of the
moon's orbit is disturbed, is the same with the force 3PK or 3IT. And
this force (by Prop. XXV) is to the force by which the moon may, in its
periodic time, be uniformly revolved in a circle about the earth at
rest, as 3IT to the radius of the circle multiplied by the number
178,725, or as IT to the radius there of multiplied by 59,575. But in
this calculus, and all that follows, I consider all the lines drawn from
the moon to the sun as parallel to the line which joins the earth and
the sun; because what inclination there is almost as much diminishes all
effects in some cases as it augments them in others; and we are now
inquiring after the mean motions of the nodes, neglecting such niceties
as are of no moment, and would only serve to render the calculus more
perplexed.
PI, PK perpendiculars upon the lines ST, Qq;
Pp a perpendicular upon the plane of the ecliptic; A, B the
moon's syzygies in the plane of the ecliptic; AZ a perpendicular let
fall upon Nn, the line of the nodes; Q, g the
quadratures of the moon in the plane of the ecliptic, and pK a
perpendicular on the line Qq lying between the quadratures. The
force of the sun to disturb the motion of the moon (by Prop. XXV) is
twofold, one proportional to the line LM, the other to the line MT, in
the scheme of that Proposition; and the moon by the former force is
drawn towards the earth, by the latter towards the sun, in a direction
parallel to the right line ST joining the earth and the sun. The former
force LM acts in the direction of the plane of the moon's orbit, and
therefore makes no change upon the situation thereof, and is upon that
account to be neglected; the latter force MT, by which the plane of the
moon's orbit is disturbed, is the same with the force 3PK or 3IT. And
this force (by Prop. XXV) is to the force by which the moon may, in its
periodic time, be uniformly revolved in a circle about the earth at
rest, as 3IT to the radius of the circle multiplied by the number
178,725, or as IT to the radius there of multiplied by 59,575. But in
this calculus, and all that follows, I consider all the lines drawn from
the moon to the sun as parallel to the line which joins the earth and
the sun; because what inclination there is almost as much diminishes all
effects in some cases as it augments them in others; and we are now
inquiring after the mean motions of the nodes, neglecting such niceties
as are of no moment, and would only serve to render the calculus more
perplexed.
Now suppose PM to represent an arc which the moon describes in the
least moment of time, and ML a little line, the half of which the moon,
by the impulse of the said force 3IT, would describe in the same time;
and joining PL, MP, let them be produced to m and l,
where they cut the plane of the ecliptic, and upon Tm let fall
the perpendicular PH. Now, since the right line ML is parallel to the
plane of the ecliptic, and therefore can never meet with the right line
ml which lies in that plane, and yet both those right lines lie
in one common plane LMPml, they will be parallel, and upon that
account the triangles LMP, lmP will be similar. And seeing MPm
lies in the plane of the orbit, in which the moon did move while in the
place P, the point m will fall upon the line Nn,
which passes through the nodes N, n, of that orbit. And
because the force by which the half of the little line LM is generated,
if the whole had been together, and at once impressed in the point P,
would have generated that whole line, and caused the moon to move in the
arc whose chord is LP; that is to say, would have transferred the moon
from the plane MPmT into the plane LPlT; therefore the
angular motion of the nodes generated by that force will be equal to the
angle mTl. But ml is to mP as ML
to MP; and since MP, because of the time given, is also given, ml
will be as the rectangle ML x mP,
that is, as the rectangle IT x mP. And if Tml is a
right angle, the angle mTl will be as
ml
Tm and therefore as
IT x Pm
Tm, that is (because Tm and mP,
TP and PH are proportional), as IT
x PH
TP; and, therefore, because TP is given,
as IT x PH. But if the angle Tml or STN is oblique, the angle mTl
will be yet less, in proportion of the sine of the angle STN to the
radius, or AZ to AT. And therefore the velocity of the nodes is as IT x
PH x AZ, or as the solid content of the sines of the three angles TPI,
PTN, and STN.
If these are right angles, as happens when the nodes are in the
quadratures, and the moon in the syzygy, the little line ml
will be removed to an infinite distance, and the angle mTl
will become equal to the angle mPl. But in this case
the angle mPl is to the angle PTM, which the moon in
the same time by its apparent motion describes about the earth, as 1 to
59,575. For the angle mPl is equal to the angle LPM,
that is, to the angle of the moon's deflexion from a rectilinear path;
which angle, if the gravity of the moon should have then ceased, the
said force of the sun 3IT would by itself have generated in that given
time; and the angle PTM is equal to the angle of the moon's deflexion
from a rectilinear path; which angle, if the force of the sun 3IT should
have then ceased, the force alone by which the moon is retained in its
orbit would have generated in the same time. And these forces (as we
have above shewn) are the one to the other as 1 to 59,575. Since,
therefore, the mean horary motion of the moon (in respect of the fixed
stars) is 32′ 56″ 27‴ 12½iv, the horary motion of the node in
this case will be 33″ 10‴ 33iv.12v. But in other
cases the horary motion will be to 33″ 10‴ 33iv.12v,
as the solid content of the sines of the three angles TPI, PTN, and STN
(or of the distances of the moon from the quadrature, of the moon from
the node, and of the node from the sun) to the cube of the radius. And
as often as the sine of any angle is changed from positive to negative,
and from negative to positive, so often must the regressive be changed
into a progressive, and the progressive into a regressive motion. Whence
it comes to pass that the nodes are progressive as often as the moon
happens to be placed between either quadrature, and the node nearest to
that quadrature. In other cases they are regressive, and by the excess
of the regress above the progress, they are monthly transferred in
antecedentia.
Cor. 1. Hence if from P and M, the extreme
points of a least arc PM, on the line Qq joining the
quadratures we let fall the perpendiculars PK, Mk, and produce
the same till they cut the line of the nodes Nn in D and d,
the horary motion of the nodes will be as the area MPDd, and
the square of the line AZ conjunctly. For let PK, PH, and AZ, be the
three said sines, viz., PK the sine of the distance of the moon from the
quadrature,
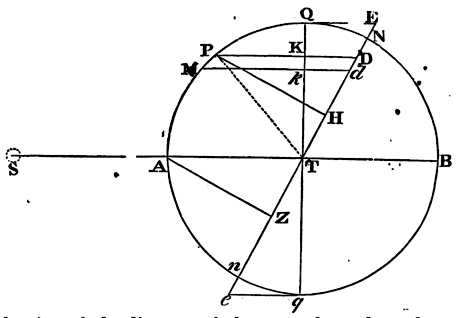 PH the sine of the distance of the moon from the node, and AZ the sine of the
distance of the node from the sun; and the velocity of the node will be
as the solid content of PK x PH x AZ. But PT is to PK as PM to Kk;
and, therefore, because PT and PM are given, Kk will be as PK.
Likewise AT is to PD as AZ to PH, and therefore PH is as the rectangle
PD x AZ; and, by compounding those proportions, PK x PH is as the solid
content Kk x PD x AZ, and PK x PH x AZ as Kk x PD x
AZ²; that is, as the area PDdM and AZ² conjunctly.
Q.E.D.
PH the sine of the distance of the moon from the node, and AZ the sine of the
distance of the node from the sun; and the velocity of the node will be
as the solid content of PK x PH x AZ. But PT is to PK as PM to Kk;
and, therefore, because PT and PM are given, Kk will be as PK.
Likewise AT is to PD as AZ to PH, and therefore PH is as the rectangle
PD x AZ; and, by compounding those proportions, PK x PH is as the solid
content Kk x PD x AZ, and PK x PH x AZ as Kk x PD x
AZ²; that is, as the area PDdM and AZ² conjunctly.
Q.E.D.
Cor. 2. In any given position of the nodes
their mean horary motion is half their horary motion in the moon's
syzygies; and therefore is to 16″ 35‴ 16iv.36v. as
the square of the sine of the distance of the nodes from the syzygies to
the square of the radius, or as AZ² to AT². For if the moon, by an
uniform motion, describes the semi-circle QAq, the sum of all
the areas PDdM, during the time of the moon's passage from Q to
M, will make up the area QMdE, terminating at the tangent QE of
the circle; and by the time that the moon has arrived at the point n,
that sum will make up the whole area EQAn described by the line
PD: but when the moon proceeds from n to q, the line
PD will fall without the circle, and describe the area nqe,
terminating at the tangent qe of the circle, which area,
because the nodes were before regressive, but are now progressive, must
be subducted from the former area, and, being itself equal to the area
QEN, will leave the semi-circle NQAn. While, therefore, the
moon describes a semi-circle, the sum of all the areas PDdM
will be the area of that semi-circle; and while the moon describes a
complete circle, the sum of those areas will be the area of the whole
circle. But the area PDdM, when the moon is in the syzygies, is
the rectangle of the arc PM into the radius PT; and the sum of all the
areas, every one equal to this area, in the time that the moon
describes a complete circle, is the rectangle of the whole circumference
into the radius of the circle; and this rectangle, being double the area
of the circle, will be double the quantity of the former sum. If,
therefore, the nodes went on with that velocity uniformly continued
which they acquire in the moon's syzygies, they would describe a space
double of that which they describe in fact; and, therefore, the mean
motion, by which, if uniformly continued, they would describe the same
space with that which they do in fact describe by an unequal motion, is
but one-half of that motion which they are possessed of in the
moon's syzygies. Wherefore since their greatest horary motion, if the
nodes are in the quadratures, is 33″ 10‴ 33iv, their mean
horary motion in this case will be 16″ 35‴ 16iv.36v.
And seeing the horary motion of the nodes is every where as AZ² and the
area PDdM conjunctly, and, therefore, in the moon's syzygies,
the horary motion of the nodes is as AZ² and the area PDdM
conjunctly, that is (because the area PDdM described in the
syzygies is given), as AZ², therefore the mean motion also will be as
AZ²; and, therefore, when the nodes are without the quadratures, this
motion will be to 16″ 35‴ 16iv.36v. as AZ² to AT².
Q.E.D.
Let Qpmaq represent an ellipsis described with the greater
axis Qq, am the lesser axis ab; QAqB a
circle circumscribed; T the earth in the common centre of both; S the
sun; p the moon moving in this ellipsis; and
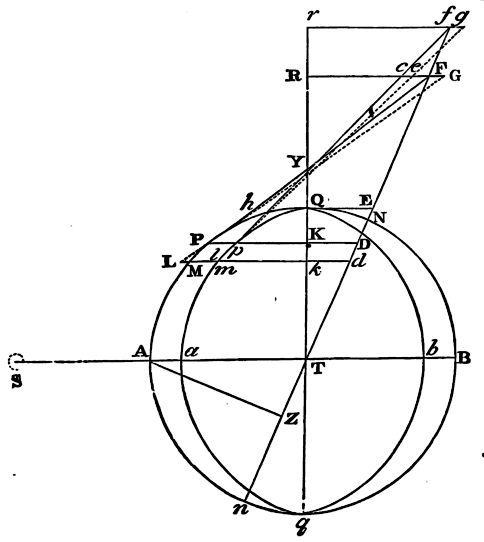 pm an arc which it describes in the
least moment of time; N and n the nodes joined by the line Nn;
pK and mk perpendiculars upon the axis Qq,
produced both ways till they meet the circle in P and M, and the line of
the nodes in D and d. And if the moon, by a radius drawn to
the earth, describes an area proportional to the time of
description, the horary motion of the node in the ellipsis will
be as the area pDdm and AZ² conjunctly.
pm an arc which it describes in the
least moment of time; N and n the nodes joined by the line Nn;
pK and mk perpendiculars upon the axis Qq,
produced both ways till they meet the circle in P and M, and the line of
the nodes in D and d. And if the moon, by a radius drawn to
the earth, describes an area proportional to the time of
description, the horary motion of the node in the ellipsis will
be as the area pDdm and AZ² conjunctly.
For let PF touch the circle in P, and produced meet TN in F; and pf
touch the ellipsis in p, and produced meet the same TN in f,
and both tangents concur in the axis TQ at Y. And let ML represent the
space which the moon, by the impulse of the above-mentioned force 3IT or
3PK, would describe with a transverse motion, in the meantime while
revolving in the circle it describes the arc PM; and ml denote
the space which the moon revolving in the ellipsis would describe in the
same time by the impulse of the same force 3IT or 3PK; and let LP and lp
be produced till they meet the plane of the ecliptic in G and g,
and FG and fg be joined, of which FG produced may cut pf,
pg, and TQ, in c, e, and R respectively; and fg
produced may cut TQ in r. Because the force 3IT or 3PK in the
circle is to the force 3IT or 3pK in the ellipsis as PK to pK,
or as AT to aT, the space ML generated by the former force
will be to the space ml generated by the latter as PK to pK;
that is, because of the similar figures PYKp and FYRc,
as FR to cR. But (because of the similar triangles PLM, PGF)
ML is to FG as PL to PG, that is (on account of the parallels Lk,
PK, GR), as pl to pe, that is (because of the
similar triangles plm, cpe) as lm to ce;
and inversely as LM is to lm, or as FR is to cR, so
is FG to ce. And therefore if fg was to ce
as fy to cY, that is, as fr to cR
(that is, as fr to FR and FR to cR conjunctly, that
is, as fT to FT, and FG to ce conjunctly), because
the ratio of FG to ce, expunged on both sides, leaves the
ratios fg to FG and fT to FT, fg would be
to FG as fT to FT; and, therefore, the angles which FG and fg
would subtend at the earth T would be equal to each other. But these
angles (by what we have shewn in the preceding Proposition) are the
motions of the nodes, while the moon describes in the circle the arc PM,
in the ellipsis the arc pm; and therefore the motions of the
nodes in the circle and in the ellipsis would be equal to each other.
Thus, I say, it would be, if fg was to ce as fY
to cY, that is, fg was equal to
ce x fY
cY. But because of the similar triangles
fgp, cep, fg is to ce as fp to cp;
and therefore fg is equal to ce
x fp
cp; and therefore the angle which fg
subtends in fact is to the former angle which FG subtends, that is to
say, the motion of the nodes in the ellipsis is to the motion of the
same in the circle as this fg or ce
x fp
cp to the fromer fg or
ce x fY
cY, that is, as fp x cY
to fY x cp, or as fp to fY, and
cY to cp; that is, if ph parallel to TN
meet FP in h, as Fh to FY and FY to FP; that is, as Fh
to FP or Dp to DP, and therefore as the area Dpmd to
the area DPMd. And, therefore, seeing (by Corol. 1, Prop. XXX)
the latter area and AZ² conjunctly are proportional to the horary motion
of the nodes in the circle, the former area and AZ² conjunctly will be
proportional to the horary motion of the nodes in the ellipsis.
Q.E.D.
Cor. Since, therefore, in any given position of
the nodes, the sum of all the areas pDdm, in the time
while the moon is carried from the quadrature to any place m,
is the area mpQEd terminated at the tangent of the
ellipsis QE; and the sum of all those areas, in one entire revolution,
is the area of the whole ellipsis; the mean motion of the nodes in the
ellipsis will be to the mean motion of the nodes in the circle as the
ellipsis to the circle; that is, as Ta to TA, or 69 to 70. And,
therefore, since (by Corol 2, Prop. XXX) the mean horary motion of the
nodes in the circle is to 16″ 35‴ 16iv.36v. as AZ²
to AT², if we take the angle 16″ 21‴ 3iv.30v. to
the angle 16″ 35‴ 16iv.36v. as 69 to 70, the mean
horary motion of the nodes in the ellipsis will be to 16″ 21‴ 3iv.30v.
as AZ² to AT²; that is, as the square of the sine of the distance of the
node from the sun to the square of the radius.
But the moon, by a radius drawn to the earth, describes the area in the
syzygies with a greater velocity than it does that in the quadratures,
and upon that account the time is contracted in the syzygies, and
prolonged in the quadratures; and together with the time the motion of
the nodes is likewise augmented or diminished. But the moment of the
area in the quadrature of the moon was to the moment thereof in the
syzygies as 10973 to 11073; and therefore the mean moment in the octants
is to the excess in the syzygies, and to the defect in the quadratures,
as 11023, the half sum of those numbers, to their half difference 50.
Wherefore since the time of the moon in the several little equal parts
of its orbit is reciprocally as its velocity, the mean time in the
octants will be to the excess of the time in the quadratures, and to the
defect of the time in the syzygies arising from this cause,
nearly as 11023 to 50. But, reckoning from the quadratures to the
syzygies, I find that the excess of the moments of the area, in the
several places above the least moment in the quadratures, is nearly as
the square of the sine of the moon's distance from the quadratures; and
therefore the difference betwixt the moment in any place, and the mean
moment in the octants, is as the difference betwixt the square of the
sine of the moon's distance from the quadratures, and the square of the
sine of 45 degrees, or half the square of the radius; and the increment
of the time in the several places between the octants and quadratures,
and the decrement thereof between the octants and syzygies, is in the
same proportion. But the motion of the nodes, while the moon describes
the several little equal parts of its orbit, is accelerated or retarded
in the duplicate proportion of the time; for
that motion, while the moon describes PM, is (caeteris paribus]
as ML, and ML is in the duplicate proportion of the time. Wherefore the
motion of the nodes in the syzygies, in the time while the moon
describes given little parts of its orbit, is diminished in the
duplicate proportion of the number 11073 to the number 11023; and the
decrement is to the remaining motion as 100 to 10973; but to the whole
motion as 100 to 11073 nearly. But the decrement in the places between
the octants and syzygies, and the increment in the places between the
octants and quadratures, is to this decrement nearly as the whole motion
in these places to the whole motion in the syzygies, and the difference
betwixt the square of the sine of the moon's distance from the
quadrature, and the half square of the radius, to the half square of the
radius conjunctly. Wherefore, if the nodes are in the quadratures, and
we take two places, one on one side, one on the other, equally distant
from the octant and other two distant by the same interval, one from the
syzygy, the other from the quadrature, and from the decrements of the
motions in the two places between the syzygy and octant we subtract the
increments of the motions in the two other places between the octant and
the quadrature, the remaining decrement will be equal to the decrement
in the syzygy, as will easily appear by computation; and therefore the
mean decrement, which ought to be subducted from the mean motion of the
nodes, is the fourth part of the decrement in the syzygy. The whole
horary motion of the nodes in the syzygies (when the moon by a radius
drawn to the earth was supposed to describe an area proportional to the
time) was 32″ 42‴ 7iv. And we have shewn that the decrement
of the motion of the nodes, in the time while the moon, now moving with
greater velocity, describes the same space, was to this motion as 100 to
11073; and therefore this decrement is 17‴ 43iv.11v.
The fourth part of which 4‴ 25iv.48v. subtracted
from the mean horary motion above found, 16″ 21‴ 3iv.30v.
leaves 16″ 16‴ 37iv.42v. their correct mean horary
motion.
If the nodes are without the quadratures, and two places are
considered, one on one side, one on the other, equally distant from the
syzygies, the sum of the motions of the nodes, when the moon is in those
places, will be to the sum of their motions, when the moon is in the
same places and the nodes in the quadratures, as AZ² to AT². And the
decrements of the motions arising from the causes but now explained will
be mutually as the motions themselves, and therefore the remaining
motions will be mutually betwixt themselves as AZ² to AT²; and the mean
motions will be as the remaining motions. And, therefore, in any given
position of the nodes, their correct mean horary motion is to 16″ 16‴ 37iv.42v.
as AZ² to AT²; that is, as the square of the sine of the distance of the
nodes from the syzygies to the square of the radius.
The yearly mean motion is the sum of all the mean horary motions
throughout the course of the year. Suppose that the node is in N, and
that, after every hour is elapsed, it is drawn back again to its former
place; so that, notwithstanding its proper motion, it may constantly
remain in the same situation with respect to the fixed stars; while in
the mean time the sun S, by the motion of the earth, is seen to leave
the node, and to proceed till it completes its apparent annual course by
an uniform motion. Let Aa represent a given least arc, which
the right line TS always drawn to the sun, by its intersection with the
circle NAn, describes in the least given moment of time; and
the mean horary motion (from what we have above shewn) will be as AZ²,
that is (because AZ and ZY are proportional), as the rectangle of AZ
into ZY, that is, as the area AZYa; and the sum of all the mean
horary motions from the beginning will be as the sum of all the areas aYZA,
that is, as the area NAZ. But the greatest AZYa is equal to the
rectangle of the arc Aa into the radius of the circle; and
therefore the sum of all these rectangles in the whole circle will be to
the like sum of all the greatest rectangles as the area of the whole
circle to the rectangle of the whole circumference into the radius, that
is, as 1 to 2. But the horary motion corresponding to that greatest
rectangle was 16″ 16‴ 37iv.42v. and this motion in
the complete course of the sidereal year, 365d.6h.9′,
amounts to 39° 38′ 7″ 50‴, and therefore the half thereof, 19° 49′ 3″
55‴, is the mean motion of the nodes corresponding to the whole circle.
And the motion of the nodes, in the time while the sun is carried from N
to A, is to 19° 49′ 3″ 55‴ as the area NAZ to the whole circle.
Thus it would be if the node was after every hour drawn back again to
its former place, that so, after a complete revolution, the sun at the
year's end would be found again in the same node which it had left when
the year begun. But, because of the motion of the node in the mean time,
the sun must needs meet the node sooner; and now it remains that we
compute the abbreviation of the time. Since, then, the sun, in the
course of the year, travels 360 degrees, and the node in the same time
by its greatest motion would be carried 39° 38′ 7″ 50‴, or 39,6355
degrees; and the mean motion of the node in any place N is to its mean
motion in its quadrature as AZ² to AT²; the motion of the sun will be to
the motion of the node in N as 360AT² to
39,6355 AZ²; that is, as 9,0827646AT² to AZ². Wherefore if we suppose
the circumference NAn of the whole circle to be divided into
little equal parts, such as Aa, the time in which the sun would
describe the little arc Aa, if the circle was quiescent, will
be to the time of which it would describe the same arc, supposing the
circle together with the nodes to be revolved about the centre T,
reciprocally as 9,0827646AT² to 9,0827646AT² + AZ²; for the time is
reciprocally as the velocity with which the little arc is described, and
this velocity is the sum of the velocities of both sun and node. If,
therefore, the sector NTA represent the time in which the sun by itself,
without the motion of the node, would describe the arc NA, and the
indefinitely small part ATa of the sector represent the little
moment of the time in which it would describe the least arc Aa;
and (letting fall aY perpendicular upon Nn) if in AZ
we take dZ of such length that the rectangle of dZ
into ZY may be to the least part ATa of the sector as AZ² to
9,0827646AT² + AZ², that is to say, that dZ may be to ½AZ as
AT² to 9,0827646AT² + AZ²; the rectangle of dZ into ZY will
represent the decrement of the time arising from the motion of the node,
while the arc Aa is described; and if the curve NdGn
is the locus where the point d is always found, the
curvilinear area NdZ will be as the whole decrement of time
while the whole arc NA is described; and, therefore, the excess of the
sector NAT above the area NdZ will be as the whole time. But
because the motion of the node in a less time is less in proportion of
the time, the area AaYZ must also be diminished in the same
proportion; which may be done by taking in AZ the line eZ of
such length, that it may be to the length of AZ as AZ² to 9,0827646AT² +
AZ²; for so the rectangle of eZ into ZY will be to the area
AZYa as the decrement of the time in which the arc Aa
is described to the whole time in which it would have been described, if
the node had been quiescent; and, therefore, that rectangle will be as
the decrement of the motion of the node. And if the curve NeFn
is the locus of the point e, the whole area NeZ,
which is the sum of all the decrements of that motion, will be
as the whole decrement thereof during the time in which the
arc AN is described; and the remaining area NAe will be as the
remaining motion, which is the true motion of the node, during the time
in which the whole arc NA is described by the joint motions of both sun
and node. Now the area of the semi-circle is to the area of the figure NeFn
found by the method of infinite series nearly as 793 to 60. But the
motion corresponding or proportional to the whole circle was
19° 49′ 3″ 55‴; and therefore the motion corresponding to double the
figure NeFn is 1° 29′ 58″ 2‴, which taken from the
former motion leaves 18° 19′ 5″ 53‴, the whole motion of the node with
respect to the fixed stars in the interval between two of its
conjunctions with the sun; and this motion subducted from the annual
motion of the sun 360°, leaves 341° 40′ 54″ 7‴, the
motion of the sun in the interval between the same conjunctions. But as
this motion is to the annual motion 360°, so is the motion of the node
but just now found 18° 19′ 5″ 53‴ to its annual motion, which will
therefore be 19° 18′ 1″ 23‴; and this is the mean motion of the nodes in
the sidereal year. By astronomical tables, it is 19° 21′ 21″ 50‴ . The
difference is less than 1/300
part of the whole motion, and seems to arise from the eccentricity of
the moon's orbit, and its inclination to the plane of the ecliptic. By
the eccentricity of this orbit the motion of the nodes is too much
accelerated; and, on the other hand, by the inclination of the orbit,
the motion of the nodes is something retarded, and reduced to its just
velocity.
In the time which is as the area NTA − NdZ (in the preceding
Fig.) that motion is as the area NAe, and is thence given; but
because the calculus is too difficult, it will be better to use the
following construction of the Problem. About the centre C, with any
interval CD, describe the circle BEFD; produce DC to A so as AB may be
to AC as the mean motion to half the mean true motion when the nodes are
in their quadratures (that is, as 19° 18′ 1″ 23‴ to 19° 49′ 3″ 55‴; and
therefore BC to AC as the difference of those motions 0° 31′ 2″ 32‴ to
the latter motion 19° 49′ 3″ 55‴, that is, as 1 to 38
3/10).
Then through the point D draw the indefinite line Gg, touching
the circle in D; and if we take the angle BCE, or BCF, equal to the
double distance of the sun from the place of the node, as found by the
mean motion, and drawing AE or AF cutting the perpendicular DG in G, we
take another angle which shall be to the whole motion of the node in the
interval between its syzygies (that is, to 9° 11′ 3″) as the tangent DG
to the whole circumference of the circle BED, and add this last
angle (for which the angle DAG may be used) to the mean motion of the
nodes, while they are passing from the quadratures to the syzygies, and
subtract it from their mean motion while they are passing from the
syzygies to the quadratures, we shall have their true motion; for the
true motion so found will nearly agree with the true motion which comes
out from assuming the times as the area NTA − NdZ, and the
motion of the node as the area NAe; as whoever will please to
examine and make the computations will find: and this is the
semi-menstrual equation of the motion of the nodes. But there is also a
menstrual equation, but which is by no means necessary for finding
of the moon's latitude; for since the variation of
the inclination of the moon's orbit to the plane of the ecliptic is
liable to a twofold inequality, the one semi-menstrual, the other
menstrual, the menstrual inequality of this variation, and the
menstrual equation of the nodes, so moderate and correct each other,
that in computing the latitude of the moon both may be neglected.
Cor. From this and the preceding Prop, it
appears that the nodes are quiescent in their syzygies, but regressive
in their quadratures, by an hourly motion of 16″ 19‴ 26iv.;
and that the equation of the motion of the nodes in the octants is 1°
30; all which exactly agree with the phaenomena of the heavens.
Mr. Machin, Astron., Prof. Gresh.. and Dr. Henry
Pemberton, separately found out the motion of the nodes by a
different method. Mention has been made of this method in another
place. Their several papers, both of which I have seen, contained two
Propositions, and exactly agreed with each other in both of them. Mr.
Machin's paper coming first to my hands, I shall here insert
it.
Let T be the earth's place, Nn the line of the moon's nodes
at any given time, KTM a perpendicular thereto, TA a right line
revolving about the centre with the same angular velocity with which
the sun and the node recede from one another, in such sort that the
angle between the quiescent right line Nn and the revolving
line TA may be always equal to the distance of the places of the sun
and node. Now if any right line TK be divided into parts TS and SK,
and those parts be taken as the mean horary motion of the sun to the
mean horary motion of the node in the quadratures, and there be taken
the right line TH, a mean proportional between the part TS and the
whole TK, this right line will be proportional to the sun's mean
motion from the node.
For let there be described the circle NKnM from the centre
T and with the radius TK, and about the same centre, with the
semi-axis TH
 and TN, let there be described an ellipsis NHnL; and in the
time in which the sun recedes from the node through the arc Na,
if there be drawn the right line Tba, the area of the sector
NTa will be the exponent of the sum of the motions of the sun
and node in the same time. Let, therefore, the extremely small arc aA
be that which the right line Tba, revolving according to the
aforesaid law, will uniformly describe in a given particle of time,
and the extremely small sector TAa will be as the sum of the
velocities with which the sun and node are carried two different ways
in that time. Now the sun's velocity is almost uniform, its inequality
being so small as scarcely to produce the least inequality in the mean
motion of the nodes. The other part of this sum, namely, the mean
quantity of the velocity of the node, is increased in the recess from
the syzygies in a duplicate ratio of the sine of its distance from the
sun (by Cor. Prop. XXXI, of this Book), and, being greatest in its
quadratures with the sun in K, is in the same ratio to the sun's
velocity as SK to TS, that is, as (the difference of the squares of TK
and TH, or) the rectangle KHM to TH². But the ellipsis NBH divides the
sector ATa, the exponent of the sum of these two velocities,
into two parts ABba and BTb, proportional to the
velocities. For produce BT to the circle in β, and from the
point B let fall upon the greater axis the perpendicular BG, which
being produced both ways may meet the circle in the points F and f;
and because the space ABba is to the sector TBb as
the rectangle ABβ to BT² (that rectangle being equal to the
difference of the squares of TA and TB, because the right line Aβ
is equally cut in T, and unequally in B), therefore when the space ABba
is the greatest of all in K, this ratio will be the same as the ratio
of the rectangle KHM to HT². But the greatest mean velocity of the
node was shewn above to be in that very ratio
to the velocity of the sun; and therefore in the quadratures the
sector ATa is divided into parts proportional to the
velocities. And because the rectangle KHM is to HT² as FBf to
BG², and the rectangle ABβ is equal to the rectangle FBf,
therefore the little area ABba, where it is greatest, is to
the remaining sector TBb as the rectangle ABβ to
BG². But the ratio of these little areas always was as the rectangle
ABβ to BT²; and therefore the little area ABba in
the place A is less than its correspondent little area in the
quadratures in the duplicate ratio of BG to BT, that is, in the
duplicate ratio of the sine of the sun's distance from the node. And
therefore the sum of all the little areas ABba, to wit, the
space ABN, will be as the motion of the node in the time in which the
sun hath been going over the arc NA since he left the node; and the
remaining space, namely, the elliptic sector NTB, will be as the sun's
mean motion in the same time. And because the mean annual motion of
the node is that motion which it performs in the time that the sun
completes one period of its course, the mean motion of the node from
the sun will be to the mean motion of the sun itself as the area of
the circle to the area of the ellipsis; that is, as the right line TK
to the right line TH, which is a mean proportional between TK and TS;
or, which comes to the same as the mean proportional TH to the right
line TS.
and TN, let there be described an ellipsis NHnL; and in the
time in which the sun recedes from the node through the arc Na,
if there be drawn the right line Tba, the area of the sector
NTa will be the exponent of the sum of the motions of the sun
and node in the same time. Let, therefore, the extremely small arc aA
be that which the right line Tba, revolving according to the
aforesaid law, will uniformly describe in a given particle of time,
and the extremely small sector TAa will be as the sum of the
velocities with which the sun and node are carried two different ways
in that time. Now the sun's velocity is almost uniform, its inequality
being so small as scarcely to produce the least inequality in the mean
motion of the nodes. The other part of this sum, namely, the mean
quantity of the velocity of the node, is increased in the recess from
the syzygies in a duplicate ratio of the sine of its distance from the
sun (by Cor. Prop. XXXI, of this Book), and, being greatest in its
quadratures with the sun in K, is in the same ratio to the sun's
velocity as SK to TS, that is, as (the difference of the squares of TK
and TH, or) the rectangle KHM to TH². But the ellipsis NBH divides the
sector ATa, the exponent of the sum of these two velocities,
into two parts ABba and BTb, proportional to the
velocities. For produce BT to the circle in β, and from the
point B let fall upon the greater axis the perpendicular BG, which
being produced both ways may meet the circle in the points F and f;
and because the space ABba is to the sector TBb as
the rectangle ABβ to BT² (that rectangle being equal to the
difference of the squares of TA and TB, because the right line Aβ
is equally cut in T, and unequally in B), therefore when the space ABba
is the greatest of all in K, this ratio will be the same as the ratio
of the rectangle KHM to HT². But the greatest mean velocity of the
node was shewn above to be in that very ratio
to the velocity of the sun; and therefore in the quadratures the
sector ATa is divided into parts proportional to the
velocities. And because the rectangle KHM is to HT² as FBf to
BG², and the rectangle ABβ is equal to the rectangle FBf,
therefore the little area ABba, where it is greatest, is to
the remaining sector TBb as the rectangle ABβ to
BG². But the ratio of these little areas always was as the rectangle
ABβ to BT²; and therefore the little area ABba in
the place A is less than its correspondent little area in the
quadratures in the duplicate ratio of BG to BT, that is, in the
duplicate ratio of the sine of the sun's distance from the node. And
therefore the sum of all the little areas ABba, to wit, the
space ABN, will be as the motion of the node in the time in which the
sun hath been going over the arc NA since he left the node; and the
remaining space, namely, the elliptic sector NTB, will be as the sun's
mean motion in the same time. And because the mean annual motion of
the node is that motion which it performs in the time that the sun
completes one period of its course, the mean motion of the node from
the sun will be to the mean motion of the sun itself as the area of
the circle to the area of the ellipsis; that is, as the right line TK
to the right line TH, which is a mean proportional between TK and TS;
or, which comes to the same as the mean proportional TH to the right
line TS.
Let the angle A be the distance of the sun from the mean place of
the node, or the sun's mean motion from the node. Then if we take the
angle B, whose tangent is to the tangent of the angle A as TH to TK,
that is,
 in the sub-duplicate ratio of the mean horary motion of the sun to the mean
horary motion of the sun from the node, when the node is in the
quadrature, that angle B will be the distance of the sun from the
node's true place. For join FT, and, by the demonstration of the last
Proportion, the angle FTN will be the distance of the sun from the
mean place of the node, and the angle ATN the distance from the true
place, and the tangents of these angles are between themselves as TK to TH.
in the sub-duplicate ratio of the mean horary motion of the sun to the mean
horary motion of the sun from the node, when the node is in the
quadrature, that angle B will be the distance of the sun from the
node's true place. For join FT, and, by the demonstration of the last
Proportion, the angle FTN will be the distance of the sun from the
mean place of the node, and the angle ATN the distance from the true
place, and the tangents of these angles are between themselves as TK to TH.
Cor. Hence the angle FTA is the equation of
the moon's nodes; and the sine of this angle, where it is greatest in
the octants, is to the radius as KH to TK + TH. But the sine of this
equation in any other place A is to the greatest sine as the sine of
the sums of the angles FTN + ATN to the radius; that is, nearly as the
sine of double the distance of the sun from the mean place of the node
(namely, 2FTN) to the radius.
If the mean horary motion of the nodes in the quadratures be 16″ 16‴
37iv.42v. that is, in a whole sidereal year, 39°
38′ 7″ 50‴, TH will be to TK in the subduplicate ratio of the number
9,0827646 to the number 10,0827646, that is, as 18,6524761 to
19,6524761. And, therefore, TH is to HK as 18,6524761 to 1; that is,
as the motion of the sun in a sidereal year to the mean motion of the
node 19° 18′ 1″ 23⅔‴.
But if the mean motion of the moon's nodes in 20 Julian years is
386° 50′ 15″, as is collected from the observations made use of in the
theory of the moon, the mean motion of the nodes in one sidereal year
will be 19° 20′ 31″ 58‴. and TH will be to HK as 360° to 19° 20′ 31″
58‴; that is, as 18,61214 to 1: and from hence the mean horary motion
of the nodes in the quadratures will come out 16″ 18‴ 48iv.
And the greatest equation of the nodes in the octants will be 1° 29′ 57″.“
Let A and a represent the syzygies; Q and q the
quadratures; N and n the nodes; P the place of the moon in its
orbit; p the orthographic projection of that place upon the
plane of the ecliptic; and mTl the momentaneous
motion of the nodes as above. If upon Tm we let fall the
perpendicular PG, and joining pG we produce it till it meet Tl
in g, and join also Pg, the angle PGp will
be the inclination of the moon's orbit to the plane of the ecliptic when
the moon is in P; and the angle Pgp will be the inclination of
the same after a small moment of time is elapsed; and therefore the
angle GPg will be the momentaneous variation of the
inclination. But this angle GPg is to the angle GTg as
TG to PG and Pp to PG conjunctly. And, therefore, if for the
moment of time we assume
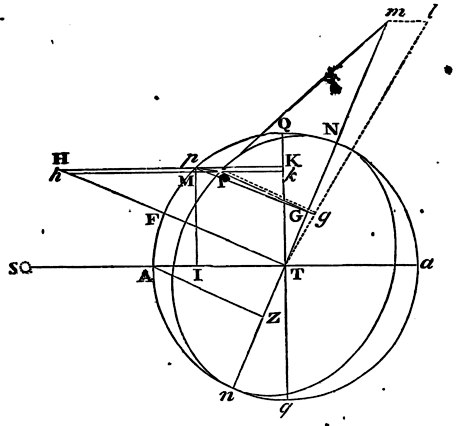 an hour, since the angle GTg (by Prop. XXX) is to the angle 33″
10‴ 33iv. as IT x PG x AZ to AT³, the angle GPg (or
the horary variation of the inclination) will be to the angle 33″ 10‴ 33iv.
as IT x AZ x TG x Pp
an hour, since the angle GTg (by Prop. XXX) is to the angle 33″
10‴ 33iv. as IT x PG x AZ to AT³, the angle GPg (or
the horary variation of the inclination) will be to the angle 33″ 10‴ 33iv.
as IT x AZ x TG x Pp
PG to AT³. Q.E.I.
And thus it would be if the moon was uniformly revolved in a circular
orbit. But if the orbit is elliptical, the mean motion of the nodes will
be diminished in proportion of the lesser axis to the greater, as we
have shewn above; and the variation of the inclination will be also
diminished in the same proportion.
Cor. 1. Upon Nn erect the
perpendicular TF, and let pM be the horary motion of the moon
in the plane of the ecliptic; upon QT let fall the perpendiculars pK,
Mk, and produce them till they meet TF in H and h;
then IT will be to AT as Kk to Mp; and TG to Hp
as TZ to AT; and, therefore, IT x TG will be equal to
Kk x Hp x TZ
Mp, that is, equal to the area HpMh
multiplied into the ratio TZ
Mp : and therefore the horary variation
of the inclination will be to 33″ 10‴ 33iv. as the area HpMh
multiplied into AZ x TZ
Mp x Pp
PG to AT³.
Cor. 2. And, therefore, if the earth and nodes
were after every hour drawn back from their new and instantly restored
to their old places, so as their situation might continue given for a
whole periodic month together, the whole variation of the inclination
during that month would be to 33″ 10‴ 33iv.
as the aggregate of all the areas HpMh, generated in
the time of one revolution of the point p (with due regard in
summing to their proper signs + −), multiplied into AZ
x TZ x Pp
PG to Mp x AT³; that
is, as the whole circle QAqa multiplied into AZ
x TZ x Pp
PG to Mp x AT³, that
is, as the circumference QAqa multiplied into AZ
x TZ x Pp
PG to 2Mp x AT².
Cor. 3. And, therefore, in a given position of
the nodes, the mean horary variation, from which, if uniformly continued
through the whole month, that menstrual variation might be generated, is
to 33″ 10‴ 33iv. as AZ x TZ x Pp
PG to 2AT², or as Pp
x AZ x TZ
1/2AT to
PG x 4AT; that is (because Pp is to PG as the sine of the
aforesaid inclination to the radius, and AZ
x TZ
1/2AT to 4AT as
the sine of double the angle ATn to four times the radius), as
the sine of the same inclination multiplied into the sine of double the
distance of the nodes from the sun to four times the square of the
radius.
Cor. 4. Seeing the horary variation of the
inclination, when the nodes are in the quadratures, is (by this Prop.)
to the angle 33″ 10‴ 33iv. as IT x AZ x
TG x Pp
PG to AT³, that is, as
IT x TG
1/2AT x
Pp
PG to 2AT, that is, as the
sine of double the distance of the moon from the quadratures multiplied
into Pp
PG to twice the radius, the sum of all
the horary variations during the time that the moon, in this situation
of the nodes, passes from the quadrature to the syzygy (that is, in the
space of 1771/6 hours)
will be to the sum of as many angles 33″ 10‴ 33iv. or 5878″,
as the sum of all the sines of double the distance of the moon from the
quadratures multiplied into Pp
PG to the sum of as many diameters;
that is, as the diameter multiplied into Pp
PG to the circumference; that is, if
the inclination be 5° 1′, as 7 x 874/10000
to 22, or as 278 to 10000. And, therefore, the whole variation, composed
out of the sum of all the horary variations in the aforesaid time, is
163″, or 2′ 43″.
Let AD be the sine of the greatest inclination, and AB the sine of the
least. Bisect BD in C; and round the centre C, with the interval BC,
describe the circle BGD. In AC take CE in the same proportion to EB
 as EB to twice BA.
And if to the time given we set off the angle AEG equal to double the distance of the nodes from the
quadratures, and upon AD let fall the perpendicular GH, AH will be the
sine of the inclination required.
as EB to twice BA.
And if to the time given we set off the angle AEG equal to double the distance of the nodes from the
quadratures, and upon AD let fall the perpendicular GH, AH will be the
sine of the inclination required.
For GE² is equal to GH² + HE² = BHD + HE² = HBD + HE² − BH² = HBD + BE²
− 2BH x BE = BE² + 2EC x BH = 2EC x AB + 2EC x BH = 2EC x AH; wherefore
since 2EC is given, GE² will be as AH. Now let AEg represent
double the distance of the nodes from the quadratures, in a given moment
of time after, and the arc Gg, on account of the given angle GEg,
will be as the distance GE. But Hh is to Gg as GH to
GC, and, therefore, Hh is as the rectangle GH x Gg, or
GH x GE, that is, as GH
GE x GE², or GH
GE x AH; that is, as AH and the sine of
the angle AEG conjunctly. If, therefore, in any one case, AH be the sine
of inclination, it will increase by the same increments as the sine of
inclination doth, by Cor. 3 of the preceding Prop. and therefore will
always continue equal to that sine. But when the point G falls upon
either point B or D, AH is equal to this sine, and therefore remains
always equal thereto. Q.E.D.
In this demonstration I have supposed that the angle BEG, representing
double the distance of the nodes from the quadratures, increaseth
uniformly; for I cannot descend to every minute circumstance of
inequality. Now suppose that BEG is a right angle, and that Gg
is in this case the horary increment of double the distance of the nodes
from the sun; then, by Cor. 3 of the last Prop. the horary variation of
the inclination in the same case will be to 33″ 10‴ 33iv. as
the rectangle of AH, the sine of the inclination, into the sine of the
right angle BEG, double the distance of the nodes from the sun, to four
times the square of the radius; that is, as AH, the
sine of the mean inclination, to four times the radius; that is, seeing
the mean inclination is about 5° 8½, as its sine 896 to 40000, the
quadruple of the radius, or as 224 to 10000. But the whole variation
corresponding to BD, the difference of the sines, is to this horary
variation as the diameter BD to the arc Gg, that is, conjunctly
as the diameter BD to the semi-circumference BGD, and as the time of
20797/10 hours, in which
the node proceeds from the quadratures to the syzygies, to one hour,
that is as 7 to 11, and 20797/10
to 1. Wherefore, compounding all these proportions, we shall have the
whole variation BD to 33″ 10‴ 33iv. as 224 x 7 x 20797/10
to 110000, that is, as 29645 to 1000; and from thence that variation BD
will come out 16′ 23½″.
And this is the greatest variation of the inclination, abstracting from
the situation of the moon in its orbit; for if the nodes are in the
syzygies, the inclination suffers no change from the various positions
of the moon. But if the nodes are in the quadratures, the inclination is
less when the moon is in the syzygies than when it is in the quadratures
by a difference of 2′ 43″, as we shewed in Cor. 4 of the preceding
Prop.; and the whole mean variation BD, diminished by 1′ 21½″, the half
of this excess, becomes 15′ 2″, when the moon is in the quadratures; and
increased by the same, becomes 17′ 45″ when the moon is in the syzygies.
If, therefore, the moon be in the syzygies, the whole variation in the
passage of the nodes from the quadratures to the syzygies will be 17′
45″; and, therefore, if the inclination be 5° 17′ 20″, when the nodes
are in the syzygies, it will be 4° 59′ 35″ when the nodes are in the
quadratures and the moon in the syzygies. The truth of all which is
confirmed by observations.
Now if the inclination of the orbit should be required when the moon is
in the syzygies, and the nodes any where between them and the
quadratures, let AB be to AD as the sine of 4° 59′ 35″ to the sine of 5°
17′ 20″, and take the angle AEG equal to double the distance of the
nodes from the quadratures; and AH will be the sine of the inclination
desired. To this inclination of the orbit the inclination of the same is
equal, when the moon is 90° distant from the nodes. In other situations
of the moon, this menstrual inequality, to which the variation of the
inclination is obnoxious in the calculus of the moon's latitude, is
balanced, and in a manner took off, by the menstrual inequality of the
motion of the nodes (as we said before), and therefore may be neglected
in the computation of the said latitude.
By these computations of the lunar motions I was willing to shew that
by the theory of gravity the motions of the moon could be calculated
from their physical causes. By the same theory I moreover found that the
annual equation of the mean motion of the moon arises from the various
dilatation which the orbit of the moon suffers from
the action of the sun according to Cor. 6, Prop. LXVI, Book 1. The force
of this action is greater in the perigeon sun, and dilates the moon's
orbit; in the apogeon sun it is less, and permits the orbit to be again
contracted. The moon moves slower in the dilated and faster in the
contracted orbit; and the annual equation, by which this inequality is
regulated, vanishes in the apogee and perigee of the sun. In the mean
distance of the sun from the earth it arises to about 11′ 50″; in other
distances of the sun it is proportional to the equation of the sun's
centre, and is added to the mean motion of the moon, while the earth is
passing from its aphelion to its perihelion, and subducted while the
earth is in the opposite semi-circle. Taking for the radius of the orbis
magnus 1000, and 167/8
for the earth's eccentricity, this equation, when of the greatest
magnitude, by the theory of gravity comes out 11′ 49″. But the
eccentricity of the earth seems to be something greater, and with the
eccentricity this equation will be augmented in the same proportion.
Suppose the eccentricity 1611/12,
and the greatest equation will be 11′ 51″.
Farther; I found that the apogee and nodes of the moon move faster in
the perihelion of the earth, where the force of the sun's action is
greater, than in the aphelion thereof, and that in the reciprocal
triplicate proportion of the earth's distance from the sun; and hence
arise annual equations of those motions proportional to the equation of
the sun's centre. Now the motion of the sun is in the reciprocal
duplicate proportion of the earth's distance from the sun; and the
greatest equation of the centre which this inequality generates is 1°
56′ 20″, corresponding to the abovementioned eccentricity of the sun, 16
11/12. But if the motion of
the sun had been in the reciprocal triplicate proportion of the
distance, this inequality would have generated the greatest equation 2°
54′ 30″; and therefore the greatest equations which the inequalities of
the motions of the moon's apogee and nodes do generate are to 2° 54′ 30″
as the mean diurnal motion of the moon's apogee and the mean diurnal
motion of its nodes are to the mean diurnal motion of the sun. Whence
the greatest equation of the mean motion of the apogee comes out 19′
43″, and the greatest equation of the mean motion of the nodes 9′ 24″.
The former equation is added, and the latter subducted, while the earth
is passing from its perihelion to its aphelion, and contrariwise when
the earth is in the opposite semi-circle.
By the theory of gravity I likewise found that the action of the sun
upon the moon is something greater when the transverse diameter of the
moon's orbit passeth through the sun than when the same is perpendicular
upon the line which joins the earth and the sun; and therefore the
moon's orbit is something larger in the former than in the latter case.
And hence arises another equation of the moon's mean motion, depending
upon the situation of the moon's apogee in respect
of the sun, which is in its greatest quantity when the moon's apogee is
in the octants of the sun, and vanishes when the apogee arrives at the
quadratures or syzygies; and it is added to the mean motion while the
moon's apogee is passing from the quadrature of the sun to the syzygy,
and subducted while the apogee is passing from the syzygy to the
quadrature. This equation, which I shall call the semi-annual, when
greatest in the octants of the apogee, arises to about 3′ 45″, so far as
I could collect from the phaenomena: and this is its quantity in the
mean distance of the sun from the earth. But it is increased and
diminished in the reciprocal triplicate proportion of the sun's
distance, and therefore is nearly 3′ 34″ when that distance is greatest,
and 3′ 56″ when least. But when the moon's apogee is without the
octants, it becomes less, and is to its greatest quantity as the sine of
double the distance of the moon's apogee from the nearest syzygy or
quadrature to the radius.
By the same theory of gravity, the action of the sun upon the moon is
something greater when the line of the moon's nodes passes through the
sun than when it is at right angles with the line which joins the sun
and the earth; and hence arises another equation of the moon's mean
motion, which I shall call the second semi-annual; and this is greatest
when the nodes are in the octants of the sun, and vanishes when they are
in the syzygies or quadratures; and in other positions of the nodes is
proportional to the sine of double the distance of either node from the
nearest syzygy or quadrature. And it is added to the mean motion of the
moon, if the sun is in antecedentia, to the node which is
nearest to him, and subducted if in consequentia; and in the
octants, where it is of the greatest magnitude, it arises to 47″ in the
mean distance of the sun from the earth, as I find from the theory of
gravity. In other distances of the sun, this equation, greatest in the
octants of the nodes, is reciprocally as the cube of the sun's distance
from the earth; and therefore in the sun's perigee it comes to about
49″, and in its apogee to about 45″.
By the same theory of gravity, the moon's apogee goes forward at the
greatest rate when it is either in conjunction with or in opposition to
the sun, but in its quadratures with the sun it goes backward; and the
eccentricity comes, in the former case, to its greatest quantity; in the
latter to its least, by Cor. 7, 8, and 9, Prop. LXVI, Book 1. And those
inequalities, by the Corollaries we have named, are very great, and
generate the principal which I call the semi-annual equation of the
apogee; and this semi-annual equation in its greatest quantity comes to
about 12° 18′, as nearly as I could collect from the phaenomena. Our
countryman, Horrox, was the first who advanced the theory of
the moon's moving in an ellipsis about the earth placed in its lower
focus. Dr. Halley improved the notion, by putting the centre
of the ellipsis in an epicycle whose centre is
uniformly revolved about the earth; and from the motion in this epicycle
the mentioned inequalities in the progress and regress of the apogee,
and in the quantity of eccentricity, do arise. Suppose the mean distance
of the moon from the earth to be divided into 100000 parts, and let T
represent the earth, and TC the moon's mean eccentricity of 5505 such
parts. Produce TC to B, so as CB may be the sine of the greatest
semi-annual equation 12° 18′ to the radius TC; and the circle BDA
 described about the centre C, with the interval CB,
will be the epicycle spoken of, in which the centre of the moon's
orbit is placed, and revolved according to the order of the letters BDA.
Set off the angle BCD equal to twice the annual argument, or twice the
distance of the sun's true place from the place of the moon's apogee
once equated, and CTD will be the semi-annual equation of the moon's
apogee, and TD the eccentricity of its orbit, tending to the place of
the apogee now twice equated. But, having the moon's mean motion, the
place of its apogee, and its eccentricity, as well as the longer axis of
its orbit 200000, from these data the true place of the moon
in its orbit, together with its distance from the earth, may be
determined by the methods commonly known.
described about the centre C, with the interval CB,
will be the epicycle spoken of, in which the centre of the moon's
orbit is placed, and revolved according to the order of the letters BDA.
Set off the angle BCD equal to twice the annual argument, or twice the
distance of the sun's true place from the place of the moon's apogee
once equated, and CTD will be the semi-annual equation of the moon's
apogee, and TD the eccentricity of its orbit, tending to the place of
the apogee now twice equated. But, having the moon's mean motion, the
place of its apogee, and its eccentricity, as well as the longer axis of
its orbit 200000, from these data the true place of the moon
in its orbit, together with its distance from the earth, may be
determined by the methods commonly known.
In the perihelion of the earth, where the force of the sun is greatest,
the centre of the moon's orbit moves faster about the centre C than in
the aphelion, and that in the reciprocal triplicate proportion of the
sun's distance from the earth. But, because the equation of the sun's
centre is included in the annual argument, the centre of the moon's
orbit moves faster in its epicycle BDA, in the reciprocal duplicate
proportion of the sun's distance from the earth. Therefore, that it may
move yet faster in the reciprocal simple proportion of the distance,
suppose that from D, the centre of the orbit, a right line DE is drawn,
tending towards the moon's apogee once equated, that is, parallel to TC;
and set off the angle EDF equal to the excess of the aforesaid annual
argument above the distance of the moon's apogee from the sun's perigee
in consequentia; or, which comes to the same thing, take the
angle CDF equal to the complement of the sun's true anomaly to 360°; and
let DF be to DC as twice the eccentricity of the orbis magnus
to the sun's mean distance from the earth, and the sun's mean diurnal
motion from the moon's apogee to the sun's mean diurnal motion from its
own apogee conjunctly, that is, as 337/8
to 1000, and 52′ 27″ 16‴ to 59′ 8″ 10‴ conjunctly, or as 3 to 100; and
imagine the centre of the moon's orbit placed in the point F to be
revolved in an epicycle whose centre is D; and radius DF, while the
point D moves in the circumference of the circle DABD: for by this means
the centre of the moon's orbit comes to
describe a certain curve line about the centre C, with a velocity which
will be almost reciprocally as the cube of the sun's distance from the
earth, as it ought to be.
The calculus of this motion is difficult, but may be rendered more easy
by the following approximation. Assuming, as above, the moon's mean
distance from the earth of 100000 parts, and the eccentricity TC of 5505
such parts, the line CB or CD will be found 1172¾, and DF 351/5
of those parts; and this line DF at the distance TC subtends the angle
at the earth, which the removal of the centre of the orbit from the
place D to the place F generates in the motion of this centre; and
double this line DF in a parallel position, at the distance of the upper
focus of the moon's orbit from the earth, subtends at the earth the same
angle as DF did before, which that removal generates in the motion of
this upper focus; but at the distance of the moon from the earth this
double line 2DF at the upper focus, in a parallel position to the first
line DF, subtends an angle at the moon, which the said removal generates
in the motion of the moon, which angle may be therefore called the
second equation of the moon's centre; and this equation, in the mean
distance of the moon from the earth, is nearly as the sine of the angle
which that line DF contains with the line drawn from the point F to the
moon, and when in its greatest quantity amounts to 2′ 25″. But the angle
which the line DF contains with the line drawn from the point F to the
moon is found either by subtracting the angle EDF from the mean anomaly
of the moon, or by adding the distance of the moon from the sun to the
distance of the moon's apogee from the apogee of the sun; and as the
radius to the sine of the angle thus found, so is 2′ 25″ to the second
equation of the centre: to be added, if the forementioned sum be less
than a semi-circle; to be subducted, if greater. And from the moon's
place in its orbit thus corrected, its longitude may be found in the
syzygies of the luminaries.
The atmosphere of the earth to the height of 35 or 40 miles refracts
the sun's light. This refraction scatters and spreads the light over the
earth's shadow; and the dissipated light near the limits of the shadow
dilates the shadow. Upon which account, to the diameter of the shadow,
as it comes out by the parallax, I add 1 or 1⅓ minute in lunar eclipses.
But the theory of the moon ought to be examined and proved from the
phenomena, first in the syzygies, then in the quadratures, and last of
all in the octants; and whoever pleases to undertake the work will find
it not amiss to assume the following mean motions of the sun and moon at
the Royal Observatory of Greenwich, to the last day of December
at noon, anno 1700, O.S. viz. The mean motion of the sun
♑ 20° 43′ 40″, and of its apogee ♋
7° 44′ 30″; the mean motion of the moon ♒
15° 21′ 00″; of its apogee, ♊ 8°
20′ 00″; and of its ascending node ♌
27° 24′ 20″; and the difference of meridians betwixt the Observatory at
Greenwich and the Royal Observatory at
Paris, Oh.9′20″: but the mean motion of the moon and
of its apogee are not yet obtained with sufficient accuracy.
The sun's force ML or PT to disturb the motions of the moon, was (by
Prop. XXV.) in the moon's quadratures, to the force of gravity with us,
as 1 to 638092,6; and the force TM − LM or 2PK in the moon's syzygies is
double that quantity. But, descending to the surface of the earth, these
forces are diminished in proportion of the distances from the centre of
the earth, that is, in the proportion of 60½ to 1; and therefore the
former force on the earth's surface is to the force of gravity as 1 to
38604600; and by this force the sea is depressed in such places as are
90 degrees distant from the sun. But by the other force, which is twice
as great, the sea is raised not only in the places directly under the
sun, but in those also which are directly opposed to it; and the sum of
these forces is to the force of gravity as 1 to 12868200. And because
the same force excites the same motion, whether it depresses the waters
in those places which are 90 degrees distant from the sun, or raises
them in the places which are directly under and directly opposed to the
sun, the aforesaid sum will be the total force of the sun to disturb the
sea, and will have the same effect as if the whole was employed in
raising the sea in the places directly under and directly opposed to the
sun, and did not act at all in the places which are 90 degrees removed
from the sun.
And this is the force of the sun to disturb the sea in any given place,
where the sun is at the same time both vertical, and in its mean
distance from the earth. In other positions of the sun, its force to
raise the sea is as the versed sine of double its altitude above the
horizon of the place directly, and the cube of the distance from the
earth reciprocally.
Cor. Since the centrifugal force of the parts
of the earth, arising from the earth's diurnal motion, which is to the
force of gravity as 1 to 289, raises the waters under the equator to a
height exceeding that under the poles by 85472 Paris feet, as
above, in Prop. XIX., the force of the sun, which we have now shewed to
be to the force of gravity as 1 to 12868200, and therefore is to that
centrifugal force as 289 to 12868200, or as 1 to 44527, will be able to
raise the waters in the places directly under and directly opposed to
the sun to a height exceeding that in the places which arc 90 degrees
removed from the sun only by one Paris foot and 1131/30
inches; for this measure is to the measure of 85472 feet as 1 to 44527.
The force of the moon to move the sea is to be deduced from its
proportion to the force of the sun, and this
proportion is to be collected from the proportion of the motions of the
sea, which are the effects of those forces. Before the mouth of the
river Avon, three miles below Bristol, the height of
the ascent of the water in the vernal and autumnal syzygies of the
luminaries (by the observations of Samuel Sturmy) amounts to
about 45 feet, but in the quadratures to 25 only. The former of those
heights arises from the sum of the aforesaid forces, the latter from
their difference. If, therefore, S and L are supposed to represent
respectively the forces of the sun and moon while they are in the
equator, as well as in their mean distances from the earth, we shall
have L + S to L − S as 45 to 25, or as 9 to 5.
At Plymouth (by the observations of Samuel Colepress)
the tide in its mean height rises to about 16 feet, and in the spring
and autumn the height thereof in the syzygies may exceed that in the
quadratures by more than 7 or 8 feet. Suppose the greatest difference of
those heights to be 9 feet, and L + S will be to L − S as 20½ to 11½, or
as 41 to 23; a proportion that agrees well enough with the former. But
because of the great tide at Bristol, we are rather to depend
upon the observations of Sturmy; and, therefore, till we
procure something that is more certain, we shall use the proportion of 9
to 5.
But because of the reciprocal motions of the waters, the greatest tides
do not happen at the times of the syzygies of the luminaries, but, as we
have said before, are the third in order after the syzygies; or
(reckoning from the syzygies) follow next after the third appulse of the
moon to the meridian of the place after the syzygies; or rather (as Sturmy
observes) are the third after the day of the new or full moon, or rather
nearly after the twelfth hour from the new or full moon, and therefore
fall nearly upon the forty-third hour after the new or full of the moon.
But in this port they fall out about the seventh hour after the appulse
of the moon to the meridian of the place; and therefore follow next
after the appulse of the moon to the meridian, when the moon is distant
from the sun, or from opposition with the sun by about 18 or 19 degrees
in consequentia. So the summer and winter seasons come not to
their height in the solstices themselves, but when the sun is advanced
beyond the solstices by about a tenth part of its whole course, that is,
by about 36 or 37 degrees. In like manner, the greatest tide is raised
after the appulse of the moon to the meridian of the place, when the
moon has passed by the sun, or the opposition thereof; by
about a tenth part of the whole motion from one greatest tide to
the next following greatest tide. Suppose that distance about 18½
degrees; and the sun's force in this distance of the moon from the
syzygies and quadratures will be of less moment to augment and diminish
that part of the motion of the sea which proceeds from the motion of the
moon than in the syzygies and quadratures themselves in the proportion
of the radius to the co-sine of double this
distance, or of an angle of 37 degrees; that is in proportion of
10000000 to 7986355; and, therefore, in the preceding analogy, in place
of S we must put 0,7986355S.
But farther; the force of the moon in the quadratures must be
diminished, on account of its declination from the equator; for the moon
in those quadratures, or rather in 18½ degrees past the quadratures,
declines from the equator by about 23° 13′; and the force of either
luminary to move the sea is diminished as it declines from the equator
nearly in the duplicate proportion of the co-sine of the declination;
and therefore the force of the moon in those quadratures is only
0.8570327L; whence we have L + 0,7986355S to 0,8570327L − 0,7986355S as
9 to 5.
Farther yet; the diameters of the orbit in which the moon should move,
setting aside the consideration of eccentricity, are one to the other as
69 to 70; and therefore the moon's distance from the earth in the
syzygies is to its distance in the quadratures, caeteris paribus,
as 69 to 70; and its distances, when 18½ degrees advanced beyond the
syzygies, where the greatest tide was excited, and when 18½ degrees
passed by the quadratures, where the least tide was produced, are to its
mean distance as 69,098745 and 69,897345 to 69½. But the force of the
moon to move the sea is in the reciprocal triplicate proportion of its
distance; and therefore its forces, in the greatest and least of those
distances, are to its force in its mean distance is 0.9830427 and
1,017522 to 1. From whence we have 1,017522L x 0,7986355S to 0,9830427 x
0,8570327L − 0,7986355S as 9 to 5; and S to L as 1 to 4,4815. Wherefore
since the force of the sun is to the force of gravity as 1 to 12868200,
the moon's force will be to the force of gravity as 1 to 2871400.
Cor. 1. Since the waters excited by the sun's
force rise to the height of a foot and 111/30
inches, the moon's force will raise the same to the height of 8 feet and
75/22 inches; and the
joint forces of both will raise the same to the height of 10½ feet; and
when the moon is in its perigee to the height of 12½ feet, and more,
especially when the wind sets the same way as the tide. And a force of
that quantity is abundantly sufficient to excite all the motions of the
sea, and agrees well with the proportion of those motions; for in such
seas as lie free and open from east to west, as in the Pacific
sea, and in those tracts of the Atlantic and Ethiopic
seas which lie without the tropics, the waters commonly rise to 6, 9,
12, or 15 feet; but in the Pacific sea, which is of a greater
depth, as well as of a larger extent, the tides are said to be greater
than in the Atlantic and Ethiopic seas; for to have
a full tide raised, an extent of sea from east to west is required of no
less than 90 degrees. In the Ethiopic sea, the waters rise to
a less height within the tropics than in the temperate zones, because of
the narrowness of the sea between Africa and the southern
parts of America. In the middle of the open sea the waters
cannot rise with out falling together, and at
the same time, upon both the eastern and western shores, when,
notwithstanding, in our narrow seas, they ought to fall on those shores
by alternate turns; upon which account there is commonly but a small
flood and ebb in such islands as lie far distant from the continent. On
the contrary, in some ports, where to fill and empty the bays
alternately the waters are with great violence forced in and out through
shallow channels, the flood and ebb must be greater than ordinary; as at
Plymouth and Chepstow Bridge in England, at
the mountains of St. Michael, and the town of Auranches,
in Normandy, and at Cambaia and Pegu in
the East Indies. In these places the sea is hurried in and out
with such violence, as sometimes to lay the shores under water, some
times to leave them dry for many miles. Nor is this force of the influx
and efflux to be broke till it has raised and depressed the waters to
30, 40, or 50 feet and above. And a like account is to be given of long
and shallow channels or straits, such as the Magellanic
straits, and those channels which environ England. The tide in
such ports and straits, by the violence of the influx and efflux, is
augmented above measure. But on such shores as lie towards the deep and
open sea with a steep descent, where the waters may freely rise and fall
without that precipitation of influx and efflux, the proportion of the
tides agrees with the forces of the sun and moon.
Cor. 2. Since the moon's force to move the sea
is to the force of gravity as 1 to 2871400, it is evident that this
force is far less than to appear sensibly in statical or hydrostatical
experiments, or even in those of pendulums. It is in the tides only that
this force shews itself by any sensible effect.
Cor. 3. Because the force of the moon to move
the sea is to the like force of the sun as 4,4815 to 1, and those forces
(by Cor. 14, Prop. LXVI, Book 1) are as the densities of the bodies of
the sun and moon and the cubes of their apparent diameters conjunctly,
the density of the moon will be to the density of the sun as 4,4815 to 1
directly, and the cube of the moon's diameter to the cube of the sun's
diameter inversely; that is (seeing the mean apparent diameters of the
moon and sun are 31′ 16½″, and 32′ 12″), as 4891 to 1000. But the
density of the sun was to the density of the earth as 1000 to 4000; and
therefore the density of the moon is to the density of the earth as 4891
to 4000, or as 11 to 9. Therefore the body of the moon is more dense and
more earthly than the earth itself.
Cor. 4. And since the true diameter of the moon
(from the observations of astronomers) is to the true diameter of the
earth as 100 to 365, the mass of matter in the moon will be to the mass
of matter in the earth as 1 to 39,788.
Cor. 5. And the accelerative gravity on the
surface of the moon will be about three times
less than the accelerative gravity on the surface of the earth.
Cor. 6. And the distance of the moon's centre
from the centre of the earth will be to the distance of the moon's
centre from the common centre of gravity of the earth and moon as 40,788
to 39,788
Cor. 7. And the mean distance of the centre of
the moon from the centre of the earth will be (in the moon's octants)
nearly 602/5 of the
great est semi-diameters of the earth; for the greatest semi-diameter of
the earth was 19658600 Paris feet, and the mean distance of
the centres of the earth and moon, consisting of 602/5
such semi-diameters, is equal to 1187379440 feet. And this distance (by
the preceding Cor.) is to the distance of the moon's centre from the
common centre of gravity of the earth and moon as 40,788 to 39,788;
which latter distance, therefore, is 1158268534 feet. And since the
moon, in respect of the fixed stars, performs its revolution in 27d.7h.43
4/9′, the versed sine of
that angle which the moon in a minute of time describes is 12752341 to
the radius 1000,000000,000000; and as the radius is to this versed sine,
so are 1158268534 feet to 14,7706353 feet. The moon, therefore, falling
towards the earth by that force which retains it in its orbit, would in
one minute of time describe 14,7706353 feet; and if we augment this
force in the proportion of 17829/40
to 17729/40, we shall
have the total force of gravity at the orbit of the moon, by Cor. Prop.
III; and the moon falling by this force, in one minute of time would
describe 14,8538067 feet. And at the 60th part of the distance of the
moon from the earth's centre, that is, at the distance of 197896573 feet
from the centre of the earth, a body falling by its weight, would, in
one second of time, likewise describe 14,8538067 feet. And, therefore,
at the distance of 19615800, which compose one mean semi-diameter of the
earth, a heavy body would describe in falling 15,11175, or 15 feet, 1
inch, and 41/11 lines,
in the same time. This will be the descent of bodies in the latitude of
45 degrees. And by the foregoing table, to be found under Prop. XX, the
descent in the latitude of Paris will be a little greater by
an excess of about ⅔ parts of a line. Therefore, by this computation,
heavy bodies in the latitude of Paris falling in vacuo will
describe 15 Paris feet, 1 inch, 425/33
lines, very nearly, in one second of time. And if the gravity be
diminished by taking away a quantity equal to the centrifugal force
arising in that latitude from the earth's diurnal motion, heavy bodies
falling there will describe in one second of time 15 feet, 1 inch, and
1½ line. And with this velocity heavy bodies do really fall in the
latitude of Paris, as we have shewn above in Prop. IV and XIX.
Cor. 8. The mean distance of the centres of the
earth and moon in the syzygies of the moon is equal to 60 of the
greatest semi-diameters of the earth, subducting only about one 30th
part of a semi- diameter: and in the moon's
quadratures the mean distance of the same centres is 605/6
such semi-diameters of the earth; for these two distances are to the
mean distance of the moon in the octants as 69 and 70 to 69½, by Prop.
XXVIII.
Cor. 9. The mean distance of the centres of the
earth and moon in the syzygies of the moon is 60 mean semi-diameters of
the earth, and a 10th part of one semi-diameter; and in the moon's
quadratures the mean distance of the same centres is 61 mean
semi-diameters of the earth, subducting one 30th part of one
semi-diameter.
Cor. 10. In the moon's syzygies its mean
horizontal parallax in the latitudes of 0, 30, 38, 45, 52, 60, 90
degrees is 57′ 20″, 57′ 16″, 57′ 14″, 57′ 12″, 57′ 10″, 57′ 8″, 57′ 4″,
respectively.
In these computations I do not consider the magnetic attraction of the
earth, whose quantity is very small and unknown: if this quantity should
ever be found out, and the measures of degrees upon the meridian, the
lengths of isochronous pendulums in different parallels, the laws of the
motions of the sea, and the moon's parallax, with the apparent diameters
of the sun and moon, should be more exactly determined from phenomena:
we should then be enabled to bring this calculation to a greater
accuracy.
If the moon's body were fluid like our sea, the force of the earth to
raise that fluid in the nearest and remotest parts would be to the force
of the moon by which our sea is raised in the places under and opposite
to the moon as the accelerative gravity of the moon towards the earth to
the accelerative gravity of the earth towards the moon, and the diameter
of the moon to the diameter of the earth conjunctly; that is, as 39,788
to 1, and 100 to 365 conjunctly, or as 1081 to 100. Wherefore, since our
sea, by the force of the moon, is raised to 83/5
feet, the lunar fluid would be raised by the force of the earth to 93
feet; and upon this account the figure of the moon would be a spheroid,
whose greatest diameter produced would pass through the centre of the
earth, and exceed the diameters perpendicular thereto by 186 feet. Such
a figure, therefore, the moon affects, and must have put on from the
beginning. Q.E.I.
Cor. Hence it is that the same face of the moon
always respects the earth; nor can the body of the moon possibly rest in
any other position, but would return always by a libratory motion to
this situation; but those librations, however, must be exceedingly slow,
because of the weakness of the forces which excite them; so that the
face of the moon, which should be always obverted to the earth, may, for
the reason assigned in Prop. XVII. be turned towards the other focus of
the moon's orbit, without being immediately drawn back, and converted
again towards the earth.
For let there be described from the centre K, with the diameter IL,
the semi-circle INL. Suppose the semi-circumference INL to be divided
into innumerable equal parts, and from the several parts N to the diameter
 IL let fall the sines NM.
Then the sums of the squares of all the sines NM will be equal to the sums
of the squares of the sines KM, and both sums together will be equal
to the sums of the squares of as many semi-diameters KN; and therefore
the sum of the squares of all the sines NM will be but half so great
as the sum of the squares of as many semi-diameters KN.
IL let fall the sines NM.
Then the sums of the squares of all the sines NM will be equal to the sums
of the squares of the sines KM, and both sums together will be equal
to the sums of the squares of as many semi-diameters KN; and therefore
the sum of the squares of all the sines NM will be but half so great
as the sum of the squares of as many semi-diameters KN.
Suppose now the circumference of the circle AE to be divided into the
like number of little equal parts, and from every such part F a
perpendicular FG to be let fall upon the plane QR, as well as the
perpendicular AH from the point A. Then the force by which the
particle F recedes from the plane QR will (by
supposition) be as that perpendicular FG; and this force multiplied by
the distance CG will represent the power of the particle F to turn the
earth round its centre. And, therefore, the power of a particle in the
place F will be to the power of a particle in the place A as FG x GC
to AH x HC; that is, as FC² to AC²: and therefore the whole power of
all the particles F, in their proper places F, will be to the power of
the like number of particles in the place A as the sum of all the FC²
to the sum of all the AC², that is (by what we have demonstrated
before), as 1 to 2. Q.E.D.
And because the action of those particles is exerted in the direction
of lines perpendicularly receding from the plane QR, and that equally
from each side of this plane, they will wheel about the circumference
of the circle of the equator, together with the adherent body of the
earth, round an axis which lies as well in the plane QR as in that of
the equator.
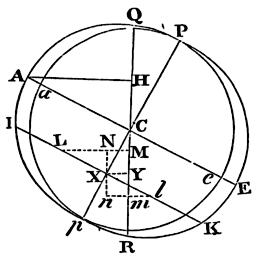
For let IK be any lesser circle parallel to the equator AE, and let Ll
be any two equal particles in this circle, situated without the sphere
Pape; and if upon the plane QR, which is at right angles with
a radius drawn to the sun, we let fall the perpendiculars LM, lm,
the total forces by which these particles recede from the plane QR
will be proportional to the perpendiculars LM, lm. Let the
right line Ll be drawn parallel to the plane Pape,
and bisect the same in X; and through the point X draw Nn
parallel to the plane QR, and meeting the perpendiculars LM, lm,
in N and n; and upon the plane QR let full the perpendicular
XY. And the contrary forces of the particles L and l to
wheel about the earth contrariwise are as LM x MC,
and lm x mC; that is, as
LN x MC + NM x MC, and ln
x mC − nm x mC; or LN
x MC + NM x MC, and LN x mC −
NM x mC, and LN x Mm −
NM x (MC + mC), the difference of the two, is the force of
both taken together to turn the earth round. The affirmative part of
this difference LN x Mm, or 2LN x NX, is to 2AH x HC, the
force of two particles of the same size situated in A, as LX² to AC²;
and the negative part NM x
(MC + mC), or 2XY x CY, is to 2AH x HC, the force of the same
two particles situated in A, as CX² to AC². And therefore the
difference of the parts, that is, the force of the two particles L and
l, taken together, to wheel the earth about, is to the force
of two particles, equal to the former and situated in the place A, to
turn in like manner the earth round, as LX² − CX² to AC². But if the
circumference IK of the circle IK is supposed to be divided into an
infinite number of little equal parts L, all the LX² will be to the
like number of IX² as 1 to 2 (by Lem. 1); and to the same number of
AC² as IX² to 2AC²; and the same number of CX² to as many AC² as 2CX²
to 2AC². Wherefore the united forces of all the particles in the
circumference of the circle IK are to the joint forces of as many
particles in the place A as IX² − 2CX² to 2AC²; and therefore (by Lem.
1) to the united forces of as many particles in the circumference of
the circle AE as IX² − 2CX² to AC².
Now if Pp, the diameter of the sphere, is conceived to be
divided into an infinite number of equal parts, upon which a like
number of circles IK are supposed to insist, the matter in the
circumference of every circle IK will be as IX²; and therefore the
force of that matter to turn the earth about will be as IX² into IX² −
2CX²; and the force of the same matter, if it was situated in the
circumference of the circle AE, would be as IX² into AC². And
therefore the force of all the particles of the whole matter situated
without the sphere in the circumferences of all the circles is to the
force of the like number of particles situated in the circumference of
the greatest circle AE as all the IX² into IX² − 2CX² to as many IX²
into AC²; that is, as all the AC² − CX² into AC² − 3CX² to as many AC²
− CX² into AC²; that is, as all the AC4 − 4AC² x CX² + 3CX4
to as many AC4 − AC² x CX²; that is, as the whole fluent
quantity, whose fluxion is AC4 − 4AC² x CX² + 3CX4,
to the whole fluent quantity, whose fluxion is AC4 − AC² x
CX²; and, therefore, by the method of fluxions, as AC4 x CX
− 4/3AC² x CX³ +
3/5CX5 to AC4
x CX − ⅓AC² x CX³; that is, if for CX we write the whole Cp,
or AC, as 4/15 AC5
to ⅔AC5; that is, as 2 to 5. Q.E.D.
For the motion of a cylinder revolved about its quiescent axis is to
the motion of the inscribed sphere revolved
together with it as any four equal squares to three circles inscribed
in three of those squares; and the motion of this cylinder is to the
motion of an exceedingly thin ring surrounding both sphere and
cylinder in their common contact as double the matter in the cylinder
to triple the matter in the ring; and this motion of the ring,
uniformly continued about the axis of the cylinder, is to the uniform
motion of the same about its own diameter performed in the same
periodic time as the circumference of a circle to double its diameter.
The middle horary motion of the moon's nodes in a circular orbit, when
the nodes are in the quadratures, was 16″ 35‴ 16iv.36v.;
the half of which, 8″ 17‴ 38iv.18v. (for the
reasons above explained) is the mean horary motion of the nodes in such
an orbit, which motion in a whole sidereal year becomes 20° 11′ 46″.
Because, therefore, the nodes of the moon in such an orbit would be
yearly transferred 20° 11′ 46″ in antecedentia; and, if there
were more moons, the motion of the nodes of every one (by Cor. 16, Prop.
LXVI. Book 1) would be as its periodic time; if upon the surface of the
earth a moon was revolved in the time of a sidereal day, the annual
motion of the nodes of this moon would be to 20° 11′ 46″ as 23h.56′,
the sidereal day, to 27d.7h.43′, the periodic time
of our moon, that is, as 1436 to 39343. And the same thing would happen
to the nodes of a ring of moons encompassing the earth, whether these
moons did not mutually touch each the other, or whether they were
molten, and formed into a continued ring, or whether that ring should
become rigid and inflexible.
Let us, then, suppose that this ring is in quantity of matter equal to
the whole exterior earth PapAPepE, which lies without
the sphere Pape (see fig. Lem. II); and because this sphere is
to that exterior earth as aC² to AC² − aC², that is
(seeing PC or aC the least semi-diameter of the earth is to AC
the greatest semi-diameter of the same as 229 to 230), as 52441 to 459;
if this ring encompassed the earth round the equator, and both together
were revolved about the diameter of the ring, the motion of the
ring (by Lem. III) would be to the motion of the inner sphere as 459 to
52441 and 1000000 to 925275 conjunctly, that is, as 4590 to 485223; and
therefore the motion of the ring would be to the sum of the motions of
both ring and sphere as 4590 to 489813. Wherefore if the ring adheres to
the sphere, and communicates its motion to the sphere, by which its
nodes or equinoctial points recede, the motion remaining in the ring
will be to its former motion as 4590 to 489813; upon which account the
motion of the equinoctial points will be diminished in the same
proportion. Wherefore the annual motion of the equinoctial points of the
body, composed of both ring and sphere, will be to the motion 20° 11′
46″ as 1436 to 39343 and 4590 to 489813 conjunctly, that is, as 100 to
292369. But the forces by which the nodes of a number of moons (as we
explained above), and therefore by which the equinoctial points of the
ring recede (that is, the forces 3IT, in fig. Prop. XXX), are in the
several particles as the distances of those particles from the plane QR;
and by these forces the particles recede from that plane: and therefore
(by Lem. II) if the matter of the ring was spread all over the surface
of the sphere, after the fashion of the figure PapAPepE,
in order to make up that exterior part of the earth, the total force or
power of all the particles to wheel about the earth round any diameter
of the equator, and therefore to move the equinoctial points, would
become less than before in the proportion of 2 to 5. Wherefore the
annual regress of the equinoxes now would be to 20° 11′ 46″ as 10 to
73092; that is, would be 9″ 56‴ 50iv.
But because the plane of the equator is inclined to that of the
ecliptic, this motion is to be diminished in the proportion of the sine
91706 (which is the co-sine of 23½ deg.) to the radius 100000; and the
remaining motion will now be 9″ 7‴ 20iv. which is the annual
precession of the equinoxes arising from the force of the sun.
But the force of the moon to move the sea was to the force of the sun
nearly as 4,4815 to 1; and the force of the moon to move the equinoxes
is to that of the sun in the same proportion. Whence the annual
precession of the equinoxes proceeding from the force of the moon comes
out 40″ 52‴ 52iv. and the total annual precession arising
from the united forces of both will be 50″ 00‴ 12iv. the
quantity of which motion agrees with the phaenomena; for the precession
of the equinoxes, by astronomical observations, is about 50″ yearly.
If the height of the earth at the equator exceeds its height at the
poles by more than 171/6
miles, the matter thereof will be more rare near the surface than at the
centre; and the precession of the equinoxes will be augmented by the
excess of height, and diminished by the greater rarity.
And now we have described the system of the sun, the earth, moon, and
planets, it remains that we add something about the comets.
As the comets were placed by astronomers above the moon, because they
were found to have no diurnal parallax, so their annual parallax is a
convincing proof of their descending into the regions of the planets;
for all the comets which move in a direct course according to the order
of the signs, about the end of their appearance become more than
ordinarily slow or retrograde, if the earth is between them and the sun;
and more than ordinarily swift, if the earth is approaching to a
heliocentric opposition with them; whereas, on the other hand, those
which move against the order of the signs, towards the end of their
appearance appear swifter than they ought to be, if the earth is between
them and the sun; and slower, and perhaps retrograde, if the earth is in
the other side of its orbit. And these appearances proceed chiefly from
the diverse situations which the earth acquires in the course of its
motion, after the same manner as it happens to the planets, which appear
sometimes retrograde, sometimes more slowly, and sometimes more swiftly,
progressive, according as the motion of the earth falls in with that of
the planet, or is directed the contrary way. If the earth move the same
way with the comet, but, by an angular motion about the sun, so much
swifter that right lines drawn from the earth to the comet converge
towards the parts beyond the comet, the comet seen from the earth,
because of its slower motion, will appear retrograde; and even if the
earth is slower than the comet, the motion of the earth being subducted,
the motion of the comet will at least appear retarded; but if the earth
tends the contrary way to that of the comet, the motion of the comet
will from thence appear accelerated; and from this apparent
acceleration, or retardation, or regressive motion, the distance of the
comet may be inferred in this manner.
 Let ♈ QA, ♈
QB, ♈ QC, be three observed
longitudes of the comet about the time of its first appearing, and
♈ QF its last observed longitude before
its disappearing. Draw the right line ABC, whose parts AB, BC,
intercepted between the right lines QA and QB, QB and QC, may be one to
the other as the two times between the three first observations. Produce
AC to G, so as AG may be to AB as the time between the first and last
observation to the time between the first and second; and join QG. Now
if the comet did move uniformly in a right line, and the earth either
stood still, or was likewise carried forwards in a right line by an
uniform motion, the angle ♈ QG
would be the longitude of the comet at the time
of the last observation. The angle, therefore, FQG, which is the
difference of the longitude, proceeds from the inequality of the motions
of the comet and the earth; and this angle, if the earth and comet move
contrary ways, is added to the angle ♈
QG, and accelerates the apparent motion of the comet; but if the comet
move the same way with the earth, it is subtracted, and either retards
the motion of the comet, or perhaps renders it retrograde, as we have
but now explained. This angle, therefore, proceeding chiefly from the
motion of the earth, is justly to be esteemed the parallax of the comet;
neglecting, to wit, some little increment or decrement that may arise
from the unequal motion of the comet in its orbit: and from this
parallax we thus deduce the distance of the comet.
Let ♈ QA, ♈
QB, ♈ QC, be three observed
longitudes of the comet about the time of its first appearing, and
♈ QF its last observed longitude before
its disappearing. Draw the right line ABC, whose parts AB, BC,
intercepted between the right lines QA and QB, QB and QC, may be one to
the other as the two times between the three first observations. Produce
AC to G, so as AG may be to AB as the time between the first and last
observation to the time between the first and second; and join QG. Now
if the comet did move uniformly in a right line, and the earth either
stood still, or was likewise carried forwards in a right line by an
uniform motion, the angle ♈ QG
would be the longitude of the comet at the time
of the last observation. The angle, therefore, FQG, which is the
difference of the longitude, proceeds from the inequality of the motions
of the comet and the earth; and this angle, if the earth and comet move
contrary ways, is added to the angle ♈
QG, and accelerates the apparent motion of the comet; but if the comet
move the same way with the earth, it is subtracted, and either retards
the motion of the comet, or perhaps renders it retrograde, as we have
but now explained. This angle, therefore, proceeding chiefly from the
motion of the earth, is justly to be esteemed the parallax of the comet;
neglecting, to wit, some little increment or decrement that may arise
from the unequal motion of the comet in its orbit: and from this
parallax we thus deduce the distance of the comet.
 Let S represent the sun, acT the orbis magnus, a
the earth's place in the first observation, c the place of the
earth in the third observation, T the place of the earth in the last
observation, and T♈ a right line
drawn to the beginning of Aries. Set off the angle ♈
TV equal to the angle ♈ QF, that
is, equal to the longitude of the comet at the time when the earth is in
T; join ac, and produce it to g, so as ag
may be to ac as AG to AC; and g will be the place at
which the earth would have arrived in the time of the last observation,
if it had continued to move uniformly in the right line ac.
Wherefore, if we draw g♈
parallel to T♈, and make the angle
♈ gV equal to the angle
♈ QG, this angle ♈
gV will be equal to the longitude of the comet seen from the
place g, and the angle TVg will be the parallax which
arises from the earth's being transferred from the place g
into the place T; and therefore V will be the place of the comet in the
plane of the ecliptic. And this place V is commonly lower than the orb
of Jupiter.
Let S represent the sun, acT the orbis magnus, a
the earth's place in the first observation, c the place of the
earth in the third observation, T the place of the earth in the last
observation, and T♈ a right line
drawn to the beginning of Aries. Set off the angle ♈
TV equal to the angle ♈ QF, that
is, equal to the longitude of the comet at the time when the earth is in
T; join ac, and produce it to g, so as ag
may be to ac as AG to AC; and g will be the place at
which the earth would have arrived in the time of the last observation,
if it had continued to move uniformly in the right line ac.
Wherefore, if we draw g♈
parallel to T♈, and make the angle
♈ gV equal to the angle
♈ QG, this angle ♈
gV will be equal to the longitude of the comet seen from the
place g, and the angle TVg will be the parallax which
arises from the earth's being transferred from the place g
into the place T; and therefore V will be the place of the comet in the
plane of the ecliptic. And this place V is commonly lower than the orb
of Jupiter.
The same thing may be deduced from the incurvation of the way of the
comets; for these bodies move almost in great circles, while their
velocity is great; but about the end of their course, when that part of
their apparent motion which arises from the parallax bears a greater
proportion to their whole apparent motion, they commonly deviate from
those circles, and when the earth goes to one side, they deviate to the
other; and this deflexion, because of its corresponding with the motion
of the earth, must arise chiefly from the parallax; and the quantity
thereof is so considerable, as, by my computation, to place the
disappearing comets a good deal lower than Jupiter. Whence it follows
that when they approach nearer to us in their perigees and perihelions
they often descend below the orbs of Mars and the inferior planets.
The near approach of the comets is farther
confirmed from the light of their heads; for the light of a celestial
body, illuminated by the sun, and receding to remote parts, is
diminished in the quadruplicate proportion of the distance; to wit, in
one duplicate proportion, on account of the increase of the distance
from the sun, and in another duplicate proportion, on account of the
decrease of the apparent diameter. Wherefore if both the quantity of
light and the apparent diameter of a comet are given, its distance will
be also given, by taking the distance of the comet to the distance of a
planet in the direct proportion of their diameters and the reciprocal
subduplicate proportion of their lights. Thus, in the comet of the year
1682, Mr. Flamsted observed with a telescope of 16 feet, and
measured with a micrometer, the least diameter of its head, 2′ 00; but
the nucleus or star in the middle of the head scarcely amounted to the
tenth part of this measure; and therefore its diameter was only 11″ or
12″; but in the light and splendor of its head it surpassed that of the
comet in the year 1680, and might be compared with the stars of the
first or second magnitude. Let us suppose that Saturn with its ring was
about four times more lucid; and because the light of the ring was
almost equal to the light of the globe within, and the apparent diameter
of the globe is about 21″, and therefore the united light of both globe
and ring would be equal to the light of a globe whose diameter is 30″,
it follows that the distance of the comet was to the distance of Saturn
as 1 to √4 inversely, and 12″ to 30 directly;
that is, as 24 to 30, or 4 to 5. Again; the comet in the month of April
1665, as Hevelius informs us, excelled almost all the fixed
stars in splendor, and even Saturn itself, as being of a much more vivid
colour; for this comet was more lucid than that other which had appeared
about the end of the preceding year, and had been compared to the stars
of the first magnitude. The diameter of its head was about 6′; but the
nucleus, compared with the planets by means of a telescope, was plainly
less than Jupiter; and sometimes judged less, sometimes judged equal, to
the globe of Saturn within the ring. Since, then, the diameters of the
heads of the comets seldom exceed 8′ or 12′, and the diameter of the
nucleus or central star is but about a tenth or perhaps fifteenth part
of the diameter of the head, it appears that these stars are generally
of about the same apparent magnitude with the planets. But in regard
that their light may be often compared with the light of Saturn, yea,
and sometimes exceeds it, it is evident that all comets in their
perihelions must either be placed below or not far above Saturn; and
they are much mistaken who remove them almost as far as the fixed stars;
for if it was so, the comets could receive no more light from our sun
than our planets do from the fixed stars.
So far we have gone, without considering the obscuration which comets
suffer from that plenty of thick smoke which encompasseth their heads,
and through which the heads always shew dull, as through a cloud; for by
how much the more a body is obscured by this
smoke, by so much the more near it must be allowed to come to the sun,
that it may vie with the planets in the quantity of light which it
reflects. Whence it is probable that the comets descend far below the
orb of Saturn, as we proved before from their parallax. But, above all,
the thing is evinced from their tails, which must be owing either to the
sun's light reflected by a smoke arising from them, and dispersing
itself through the aether, or to the light of their own heads. In the
former case, we must shorten the distance of the comets, lest we be
obliged to allow that the smoke arising from their heads is propagated
through such a vast extent of space, and with such a velocity and
expansion as will seem altogether incredible; in the latter case, the
whole light of both head and tail is to be ascribed to the central
nucleus. But, then, if we suppose all this light to be united and
condensed within the disk of the nucleus, certainly the nucleus will by
far exceed Jupiter itself in splendor, especially when it emits a very
large and lucid tail. If, therefore, under a less apparent diameter, it
reflects more light, it must be much more illuminated by the sun, and
therefore much nearer to it; and the same argument will bring down the
heads of comets sometimes within the orb of Venus, viz., when, being hid
under the sun's rays, they emit such huge and splendid tails, like beams
of fire, as sometimes they do; for if all that light was supposed to be
gathered together into one star, it would sometimes exceed not one Venus
only, but a great many such united into one.
Lastly; the same thing is inferred from the light of the heads, which
increases in the recess of the comets from the earth towards the sun,
and decreases in their return from the sun towards the earth; for so the
comet of the year 1665 (by the observations of Hevelius), from
the time that it was first seen, was always losing of its apparent
motion, and therefore had already passed its perigee; but yet the
splendor of its head was daily in creasing, till, being hid under the
sun's rays, the comet ceased to appear. The comet of the year 1683 (by
the observations of the same Hevelius), about the end of July,
when it first appeared, moved at a very slow rate, advancing only about
40 or 45 minutes in its orb in a day's time; but from that time its
diurnal motion was continually upon the increase, till September
4, when it arose to about 5 degrees; and therefore, in all this interval
of time, the comet was approaching to the earth. Which is like wise
proved from the diameter of its head, measured with a micrometer; for, August
6, Hevelius found it only 6′ 05″, including the coma,
which, September 2 he observed to be 9′ 07″, and therefore its
head appeared far less about the beginning than towards the end of the
motion; though about the beginning, because nearer to the sun, it
appeared far more lucid than towards the end, as the same Hevelius
declares. Wherefore in all this interval of time, on account of its
recess from the sun, it decreased in splendor,
notwithstanding its access towards the earth. The comet of the year
1618, about the middle of December, and that of the year 1680,
about the end of the same month, did both move with their greatest
velocity, and were therefore then in their perigees; but the greatest
splendor of their heads was seen two weeks before, when they had just
got clear of the sun's rays; and the greatest splendor of their tails a
little more early, when yet nearer to the sun. The head of the former
comet (according to the observations of Cysatus), December
1, appeared greater than the stars of the first magnitude; and, December
16 (then in the perigee), it was but little diminished in magnitude, but
in the splendor and brightness of its light a great deal. January
7, Kepler, being uncertain about the head, left off observing.
December 12, the head of the latter comet was seen and observed
by Mr. Flamsted, when but 9 degrees distant from the sun;
which is scarcely to be done in a star of the third magnitude. December
15 and 17, it appeared as a star of the third magnitude, its lustre
being diminished by the brightness of the clouds near the setting sun. December
26, when it moved with the greatest velocity, being almost in its
perigee, it was less than the mouth of Pegasus, a star of the
third magnitude. January 3, it appeared as a star of the
fourth. January 9, as one of the fifth. January 13,
it was hid by the splendor of the moon, then in her increase. January
25, it was scarcely equal to the stars of the seventh magnitude. If we
compare equal intervals of time on one side and on the other from the
perigee, we shall find that the head of the comet, which at both
intervals of time was far, but yet equally, removed from the earth, and
should have therefore shone with equal splendor, appeared brightest on
the side of the perigee towards the sun, and disappeared on the other.
Therefore, from the great difference of light in the one situation and
in the other, we conclude the great vicinity of the sun and comet in the
former; for the light of comets uses to be regular, and to appear
greatest when the heads move fastest, and are therefore in their
perigees; excepting in so far as it is increased by their nearness to
the sun.
Cor. 1. Therefore the comets shine by the sun's light, which they reflect.
Cor. 2. From what has been said, we may
likewise understand why comets are so frequently seen in that hemisphere
in which the sun is, and so seldom in the other. If they were visible in
the regions far above Saturn, they would appear more frequently in the
parts opposite to the sun; for such as were in those parts would be
nearer to the earth, whereas the presence of the sun must obscure and
hide those that appear in the hemisphere in which he is. Yet, looking
over the history of comets, I find that four or five times more have
been seen in the hemisphere towards the sun than in the opposite
hemisphere; besides, without doubt, not a few, which have been hid by
the light of the sun: for comets descending into
our parts neither emit tails, nor are so well illuminated by the sun, as
to discover themselves to our naked eyes, until they are come nearer to
us than Jupiter. But the far greater part of that spherical space, which
is described about the sun with so small an interval, lies on that side
of the earth which regards the sun; and the comets in that greater part
are commonly more strongly illuminated, as being for the most part
nearer to the sun.
Cor. 3. Hence also it is evident that the
celestial spaces are void of resistance; for though the comets are
carried in oblique paths, and some times contrary to the course of the
planets, yet they move every way with the greatest freedom, and preserve
their motions for an exceeding long time, even where contrary to the
course of the planets. I am out in my judgment if they are not a sort of
planets revolving in orbits returning into themselves with a perpetual
motion; for, as to what some writers contend, that they are no other
than meteors, led into this opinion by the perpetual changes that happen
to their heads, it seems to have no foundation; for the heads of comets
are encompassed with huge atmospheres, and the lowermost parts of these
atmospheres must be the densest; and therefore it is in the clouds only,
not in the bodies of the comets them selves, that these changes are
seen. Thus the earth, if it was viewed from the planets, would, without
all doubt, shine by the light of its clouds, and the solid body would
scarcely appear through the surrounding clouds. Thus also the belts of
Jupiter are formed in the clouds of that planet, for they change their
position one to another, and the solid body of Jupiter is hardly to be
seen through them; and much more must the bodies of comets be hid under
their atmospheres, which are both deeper and thicker.
This proposition appears from Cor. 1, Prop. XIII, Book 1, compared with
Prop. VIII, XII, and XIII, Book III.
Cor. 1. Hence if comets are revolved in orbits
returning into themselves, those orbits will be ellipses; and their
periodic times be to the periodic times of the planets in the
sesquiplicate proportion of their principal axes. And therefore the
comets, which for the most part of their course are higher than the
planets, and upon that account describe orbits with greater axes, will
require a longer time to finish their revolutions. Thus if the axis of a
comet's orbit was four times greater than the axis of the orbit of
Saturn, the time of the revolution of the comet would be to the time of
the revolution of Saturn, that is, to 30 years, as 4 √4
(or 8) to 1, and would therefore be 240 years.
Cor. 2. But their
orbits will be so near to parabolas, that parabolas may be used for them
without sensible error.
Cor. 3. And, therefore, by Cor. 7, Prop. XVI,
Book 1, the velocity of every comet will always be to the velocity of
any planet, supposed to be revolved at the same distance in a circle
about the sun, nearly in the subduplicate proportion of double the
distance of the planet from the centre of the sun to the distance of the
comet from the sun's centre, very nearly. Let us suppose the radius of
the orbis manus, or the greatest semidiameter of the ellipsis
which the earth describes, to consist of 100000000 parts; and then the
earth by its mean diurnal motion will describe 1720212 of those parts,
and 71675½ by its horary motion. And therefore the comet, at the same
mean distance of the earth from the sun, with a velocity which is to the
velocity of the earth as √2 to 1, would by
its diurnal motion describe 2432747 parts, and 101364½ parts by its
horary motion. But at greater or less distances both the diurnal and
horary motion will be to this diurnal and horary motion in the
reciprocal subduplicate proportion of the distances, and is therefore
given.
Cor. 4. Wherefore if the latus rectum
of the parabola is quadruple of the radius of the orbis magnus,
and the square of that radius is sup posed to consist of 100000000
parts, the area which the comet will daily describe by a radius drawn to
the sun will be 1216373½ parts, and the horary area will be 50682¼
parts. But, if the latus rectum is greater or less in any
proportion, the diurnal and horary area will be less or greater in the
subduplicate of the same proportion reciprocally.
Let those points be A, B, C, D, E, F, &c., and from the same to
any right line HN, given in position, let fall as many perpendiculars
AH, BI, CK, DL, EM, FN, &c.
| b |
|
2b |
|
3b |
|
4b |
|
5b |
|
c |
|
2c |
|
3c |
|
4c |
|
|
|
d |
|
2d |
|
3d |
|
|
|
|
|
e |
|
2e |
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
Case 1. If HI, IK, KL, &c., the intervals
of the points H, I, K, L, M, N, &c., are equal, take b, 2b, 3b,
4b, 5b, &c., the first differences of the perpendiculars AH,
BI, CK, &c.; their second differences c, 2c, 3c, 4c, &c.;
their third, d, 2d, 3d, &c., that is to say, so as AH − BI
may be = b, BI − CK = 2b, CK
− DL = 3b, DL + EM = 4b, − EM + FN = 5b,
&c.; then b − 2b = c, &c., and so
on to the last difference, which is here f. Then, erecting any
perpendicular RS, which may be considered as an ordinate of the curve
required, in order to find the length of this ordinate, suppose the
intervals HI, IK, KL, LM, &c., to be units, and let AH = a,
−HS = p, ½p into −IS = q, ⅓q into
+ SK = r, ¼r into + SL = s,
1/5s
into + SM = t; proceeding, to wit, to ME, the last
perpendicular but one, and prefixing negative signs before the terms HS,
IS, &c., which lie from S towards A; and affirmative signs before
the terms SK, SL, &c., which lie on the other side of the point S;
and, observing well the signs, RS will be = a + bp + cq + dr + es
+ ft, + &c.
Case 2. But if HI, IK, &c., the intervals
of the points H, I, K, L, &c.. are unequal, take b, 2b, 3b, 4b,
5b, &c., the first differences of the perpendiculars AH, BI,
CK, &c., divided by the intervals between those perpendiculars; c,
2c, 3c, 4c, &c., their second differences, divided by the
intervals between every two; d, 2d, 3d, &c., their third
differences, divided by the intervals between every three; e, 2e,
&c., their fourth differences, divided by the intervals between
every four; and so forth; that is, in such manner, that b may
be =AH-BI
HI, 2b=BI-CK
IK, 3b=CK-DL
KL, &c., then c =
b-2b
HK, 2c=2b-3b
IL, 3c=3b-4b
KM, &c., then d=
c-2c
HL, 2d=2c-3c
IM, &c. And those differences being
found, let AH be = a, − HS = p, p into −IS = q,
q into + SK = r, r into + SL = s, s into + SM
= t; proceeding, to wit, to ME, the last perpendicular but
one: and the ordinate RS will be = a + bp + cq + dr + es + ft,
+ &c.
Cor. Hence the areas of all curves may be
nearly found; for if some number of points of the curve to be squared
are found, and a parabola be supposed to be drawn through those points,
the area of this parabola will be nearly the same with the area of the
curvilinear figure proposed to be squared: but the parabola can be
always squared geometrically by methods vulgarly known.
Let HI, IK, KL, LM (in the preceding Fig.), represent the times between
the observations; HA, IB, KC, LD, ME, five observed longitudes of the
comet; and HS the given time between the first observation and the
longitude required. Then if a regular curve ABCDE is supposed to be
drawn through the points A, B, C, D, E, and the ordinate RS is found out
by the preceding lemma, RS will be the longitude required.
After the same method, from five observed
latitudes, we may find the latitude to a given time.
If the differences of the observed longitudes are small, suppose of 4
or 5 degrees, three or four observations will be sufficient to find a
new longitude and latitude; but if the differences are greater, as of 10
or 20 degrees, five observations ought to be used.
From the given point P suppose any right line PD to be drawn to either
of the right lines given, as AB; and produce the same towards AC, the
other given right line, as far as E, so as PE may be to PD in the given
proportion. Let EC be parallel to AD. Draw CPB, and PC will be to PB as
PE to PD. Q.E.F.
For if we join EO, cutting the parabolic arc ABC in Y, and draw μX
touching the same arc in the vertex μ, and meeting EO in X,
the curvilinear area AEXμA will be to the curvilinear area ACYμA
as AE to AC; and, therefore, since the triangle ASE is to the triangle
ASC in the same proportion, the whole area ASEXμA will be to
the whole area ASCYμA as
 AE to AC. But, because ξO is to SO as 3 to 1, and EO to XO in the
same proportion, SX will be parallel to EB; and, therefore, joining BX,
the triangle SEB will be equal to the triangle XEB. Wherefore if to the
area ASEXμA we add the triangle EXB, and from the sum subduct
the triangle SEB, there will remain the area ASBXμA, equal to
the area ASEXμA, and therefore in proportion to the area ASCYμA
as AE to AC. But the area ASBYμA is nearly equal to the area
ASBXμA; and this area ASBYμA is to the area ASCYμA
as the time of description of the arc AB to the time of description of
the whole arc AC; and, therefore, AE is to AC nearly in the proportion
of the times. Q.E.D.
AE to AC. But, because ξO is to SO as 3 to 1, and EO to XO in the
same proportion, SX will be parallel to EB; and, therefore, joining BX,
the triangle SEB will be equal to the triangle XEB. Wherefore if to the
area ASEXμA we add the triangle EXB, and from the sum subduct
the triangle SEB, there will remain the area ASBXμA, equal to
the area ASEXμA, and therefore in proportion to the area ASCYμA
as AE to AC. But the area ASBYμA is nearly equal to the area
ASBXμA; and this area ASBYμA is to the area ASCYμA
as the time of description of the arc AB to the time of description of
the whole arc AC; and, therefore, AE is to AC nearly in the proportion
of the times. Q.E.D.
Cor. When the point B falls upon the vertex μ
of the parabola, AE is to AC accurately in the proportion of the times.
If we join μξ cutting AC in δ, and in it take ξn
in proportion to μB as 27MI to 16Mμ, and draw Bn,
this Bn will cut the chord AC, in the proportion of the times,
more accurately than before; but the point n is to be taken
beyond or on this side the point ξ, according as the point B
is more or less distant from the principal vertex of the parabola than
the point μ.
For 4Sμ is the latus rectum of the parabola belonging to the
vertex μ.
For if the comet with the velocity which it hath in μ was in
the said time supposed to move uniformly forward in the right line which
touches the parabola in μ, the area which it would describe by
a radius drawn to the point's would be equal to the parabolic area ASCμA;
and therefore the space contained under the length described in the
tangent and the length Sμ would be to the space contained under
the lengths AC and SM as the area ASCμA
to the triangle ASC, that is, as SN to SM. Wherefore AC is to the length
described in the tangent as Sμ to SN. But since the velocity of
the comet in the height SP (by Cor. 6, Prop. XVI., Book I) is to the
velocity of the same in the height Sμ in the reciprocal
subduplicate proportion of SP to Sμ, that is, in the proportion
of Sμ to SN, the length described with this velocity will be to
the length in the same time described in the tangent as Sμ to
SN. Wherefore since AC, and the length described with this new velocity,
are in the same proportion to the length described in the tangent, they
mast be equal betwixt themselves. Q.E.D.
Cor. Therefore a comet, with that velocity
which it hath in the height Sμ + ⅔Iμ, would in the
same time describe the chord AC nearly.

For in the same time that the comet would require to describe the
parabolic arc AC, it would (by the last Lemma), with that velocity which
it hath in the height SP, describe the chord AC; and, therefore (by Cor.
7, Prop. XVI, Book 1), if it was in the same time supposed to revolve by
the force of its own gravity in a circle whose semi-diameter was SP, it
would describe an arc of that circle, the length of which would be to
the chord of the parabolic arc AC in the subduplicate proportion of 1 to
2. Wherefore if with that weight, which in the height SP it hath towards
the sun, it should fall from that height towards the sun, it would (by
Cor. 9, Prop. XVI, Book 1) in half the said time describe a space equal
to the square of half the said chord applied to quadruple the height SP,
that is, it would describe the space AI2
4SP. But since the weight of the comet
towards the sun in the height SN is to the weight of the same towards
the sun in the height SP as SP to Sμ, the comet, by the weight
which it hath in the height SN, in falling from that height towards the
sun, would in the same time describe the space
AI2
4Sμ; that is, a space equal to the length
Iμ or μM . Q.E.D.
This being a Problem of very great difficulty, I tried many methods of
resolving it; and several of these Problems, the composition whereof I
have given in the first Book, tended to this purpose. But afterwards I
contrived the following solution, which is something more simple.
Select three observations distant one from another by intervals of time
nearly equal; but let that interval of time in which the comet moves
more slowly be somewhat greater than the other; so, to wit, that the
difference of the times may be to the sum of the times as the sum of the
 times to about 600 days; or that the point E may fall upon M nearly,
and may err therefrom rather towards I than
towards A. If such direct observations are not at hand, a new place of
the comet must be found, by Lem. VI.
times to about 600 days; or that the point E may fall upon M nearly,
and may err therefrom rather towards I than
towards A. If such direct observations are not at hand, a new place of
the comet must be found, by Lem. VI.
Let S represent the sun; T, t, τ, three places of the earth
in the orbis magnus; TA, tB, τC, three
observed longitudes of the comet; V the time between the first
observation and the second; W the time between the second and the third;
X the length which in the whole time V + W
 the comet might describe with that velocity which it hath in the mean
distance of the earth from the sun, which length is to be found by Cor.
3, Prop. XL, Book III; and tV a
perpendicular upon the chord Tτ. In the mean observed longitude
tB take at pleasure the point B, for the place of the comet in
the plane of the ecliptic; and from thence, towards the sun S, draw the
line BE, which may be to the perpendicular tV as the content
under SB and St² to the cube of the hypothenuse of the right
angled triangle, whose sides are SB, and the tangent of the latitude of
the comet in the second observation to the radius tB. And
through the point E (by Lemma VII) draw the right line AEC, whose parts
AE and EC, terminating in the right lines TA and τC, may be
one to the other as the times V and W: then A and C will be nearly the
places of the comet in the plane of the ecliptic in the first and third
observations, if B was its place rightly assumed in the second.
the comet might describe with that velocity which it hath in the mean
distance of the earth from the sun, which length is to be found by Cor.
3, Prop. XL, Book III; and tV a
perpendicular upon the chord Tτ. In the mean observed longitude
tB take at pleasure the point B, for the place of the comet in
the plane of the ecliptic; and from thence, towards the sun S, draw the
line BE, which may be to the perpendicular tV as the content
under SB and St² to the cube of the hypothenuse of the right
angled triangle, whose sides are SB, and the tangent of the latitude of
the comet in the second observation to the radius tB. And
through the point E (by Lemma VII) draw the right line AEC, whose parts
AE and EC, terminating in the right lines TA and τC, may be
one to the other as the times V and W: then A and C will be nearly the
places of the comet in the plane of the ecliptic in the first and third
observations, if B was its place rightly assumed in the second.
Upon AC, bisected in I, erect the perpendicular Ii. Through B
draw the obscure line Bi parallel to AC. Join the obscure line
Si, cutting AC in λ, and complete the parallelogram iI
λμ. Take Iσ equal to 3Iλ; and through the sun
S draw the obscure line σξ equal to 3Sσ + 3iλ.
Then, cancelling the letters A, E, C, I, from the point B towards the
point ξ, draw the new obscure line BE, which may be to the
former BE in the duplicate proportion of the distance BS to the quantity
Sμ + ⅓iλ. And through the point E draw again the right
line AEC by the same rule as before; that is, so as its parts AE and EC
may be one to the other as the times V and W between the observations.
Thus A and C will be the places of the comet more accurately.
Upon AC, bisected in I, erect the perpendiculars AM, CN, IO, of which
AM and CN may be the tangents of the latitudes in the first and third
observations, to the radii TA and τC. Join MN, cutting IO in
O. Draw the rectangular parallelogram iIλμ, as
before. In IA produced take ID equal to Sμ + ⅔iλ. Then
in MN, towards N, take MP, which may be to the above found length X in
the subduplicate proportion of the mean distance of the earth from the
sun (or of the semi-diameter of the orbis magnus) to the
distance OD. If the point P fall upon the point N; A, B, and C, will be
three places of the comet, through which its orbit is to be described in
the plane of the ecliptic. But if the point P falls not upon the point
N, in the right line AC take CG equal to NP, so as the points G and P
may lie on the same side of the line NC.
By the same method as the points E, A, C, G, were found from the
assumed point B, from other points b and β assumed
at pleasure, find out the new points e, a, c, g; and ε,
α, κ, γ. Then through G, g, and γ, draw the
circumference of a circle Ggγ, cutting the right line τC
in Z: and Z will he one place of the comet in the plane of the ecliptic.
And in AC, ac, ακ, taking AF, af, αΦ, equal
respectively to CG, cg, κγ; through the points F, f,
and Φ, draw the circumference of a circle FfΦ,
cutting the right line AT in X; and the point X will be another place of
the comet in the plane of the ecliptic. And at
the points X and Z, erecting the tangents of the latitudes of the comet
to the radii TX and τZ, two places of the comet in its own
orbit will be determined. Lastly, if (by Prop. XIX., Book 1) to the
focus S a parabola is described passing through those two places, this
parabola will be the orbit of the comet. Q.E.I.
The demonstration of this construction follows from the preceding
Lemmas, because the right line AC is cut in E in the proportion of the
times, by Lem. VII., as it ought to be, by Lem. VIII.; and BE; by Lem.
XI., is a portion of the right line BS or Bξ in the plane of
the ecliptic, intercepted between the arc ABC and the chord AEC; and MP
(by Cor. Lem. X.) is the length of the chord of that arc, which the
comet should describe in its proper orbit between the first and third
observation, and therefore is equal to MN, providing B is a true place
of the comet in the plane of the ecliptic.
But it will be convenient to assume the points B, b, β, not
at random, but nearly true. If the angle AQt, at which the
projection of the orbit in the plane of the ecliptic cuts the right line
tB, is rudely known, at that angle with Bt draw the
obscure line AC, which may be to 4/3Tτ
in the subduplicate proportion of SQ, to St; and, drawing the
right line SEB so as its part EB may be equal to the length Vt,
the point B will be determined, which we are to use for the first time.
Then, cancelling the right line AC, and drawing anew AC according to the
preceding construction, and, moreover, finding the length MP, in tB
take the point b, by this rule, that, if TA and τC
intersect each other in Y, the distance Yb may be to the
distance YB in a proportion compounded of the proportion of MP to MN,
and the subduplicate proportion of SB to Sb. And by the same
method you may find the third point β, if you please to repeat
the operation the third time; but if this method is followed, two
operations generally will be sufficient; for if the distance Bb
happens to be very small, after the points F, f, and G, g,
are found, draw the right lines Ff and Gg, and they
will cut TA and τC in the points required, X and Z.
1680, Dec.
12
21
24
26
29
30
1681, Jan. 5
9
10
13
25
30
Feb. 2
5
|
Time |
sun's
Longitude |
Comet's |
| Appar. |
True. |
Longitude. |
Lat. N. |
h. ″
4.46
6.32½
6.12
5.14
7.55
8.02
5.51
6.49
5.54
6.56
7.44
8.07
6.20
6.50
|
h. ' ″
4.46.0
6.36.59
6.17.52
5.20.44
8.03.02
8.10.26
6.01.38
7.00.53
6.06.10
7.08.55
7.58.42
8.21.53
6.34.51
7.04.41
|
° ' ″
♑ 1.51.23
11.06.44
14.09.26
16.09.22
19.19.43
20.21.09
26.22.18
♒ 0.29.02
1.27.43
4.33.20
16.45.36
21.49.58
24.46.59
27.49.51
|
° ' ″
♑ 6.32.30
♒ 5.08.12
18.49.23
28.24.13
♓ 13.10.41
17.38.20
♈ 8.48.53
18.44.04
20.40.50
25.59.48
♉ 9.35.0
13.19.51
15.13.53
16.59.06
|
° ' ″
8.25. 0
21.42.13
25.23. 5
27.00.52
28.09.58
28.11.53
26.15. 7
24.11.56
23.43.52
22.17.28
17.56.30
16.42.18
16.04. 1
15.27. 3
|
To these you may add some observations of mine.
1681, Feb. 25
27
Mar. 1
2
5
7
9
|
Ap.
Time. |
Comet's |
|
Longitude |
Lat. N. |
h. '
8.30
8.15
11. 0
8. 0
11.30
9.30
8.30
|
° ' ″
♉ 26.18.35
27.04.30
27.52.42
28.12.48
29.18. 0
♊ 0. 4. 0
0. 43. 4
|
° ' ″
12.46.46
12.36.12
12.23.40
12.19.38
12.03.16
11.57. 0
11.45.52
|
These observations were made by a telescope of 7 feet, with a
micrometer and threads placed in the focus of the telescope; by which
instruments we determined the positions both of the fixed stars among
themselves, and of the comet in respect of the fixed stars. Let A
represent the star of the fourth magnitude in the left heel of Perseus
(Bayer's' ο), B the following star of the third magnitude in
the left foot (Bayer's ζ), C a star of the sixth magnitude (Bayer's
n) in the heel of the same foot, and D, E, F, G, H, I, K, L, M,
N, O, Z, α, β, γ, δ, other smaller stars in the same foot; and
let p, P, Q, R, S, T, V, X, represent the places of the comet
in the observations above set down; and, reckoning the distance AB of 80
7/12 parts, AC was 52¼ of
those parts; BC, 585/6;
AD, 575/12; BD, 82
6/11; CD, 23⅔; AE, 294/7;
CE, 57½; DE, 4911/12;
AI, 277/12; BI, 52
1/6; CI, 367/12;
DI, 535/11; AK, 38⅔; BK,
43; CK, 315/9; FK, 29;
FB, 23; FC, 36¼; AH, 186/7;
DH, 507/8; BN, 465/12;
CN, 31⅓; BL, 455/12; NL,
315/7. HO was to HI as 7
to 6, and, produced, did pass between the stars D and E, so as the
distance of the star D from this right line was 1/6CD.
LM was to LN as 2 to 9, and, produced, did pass through the star H. Thus
were the positions of the fixed stars determined in respect of one
another.
Mr. Pound has since observed a second time the positions of
those fixed stars amongst themselves, and collected their longitudes and
latitudes according to the following table.
The
fixed
stars. |
Their
Longitudes |
Latitude
North. |
The
fixed
stars. |
Their
Longitudes |
Latitude
North. |
A
B
C
E
F
G
H
I
K
|
° ' ″
♉ 26.41.50
28.40.23
27.58.30
26.27.17
28.28.37
26.56. 8
27.11.45
27.25. 2
27.42. 7
|
° ' ″
♉ 12. 8.36
11.17.54
12.40.25
12.52. 7
11.52.22
14.4.58
12.2. 1
11.53.11
11.53.26
|
L
M
N
Z
α
β
γ
δ
|
° ' ″
♉ 29.33.34
29.18.54
28.48.29
29.44.48
29.52. 3
♊ 0. 8.23
0.40.10
1. 3.20
|
° ' ″
12. 7.48
12. 7.20
12.31. 9
11.57.13
11.55.48
11.48.53
11.55.18
11.30.42
|
The positions of the comet to these fixed stars were observed to be as follow:
Friday, February 25, O.S. at 8½h. P. M. the
distance of the comet in p from the star E was less than
3/13AE, and greater than
1/5AE, and therefore nearly
equal to 3/14AE; and
the angle ApE was a little obtuse, but almost right. For from
A, letting fall a perpendicular on pE; the distance of the
comet from that perpendicular was 1/5pE.
The same night, at 9½h., the distance of the comet in P from
the star E was greater than 1
41/2 AE, and less
than 1
51/4 AE, and
therefore nearly equal to 1
47/8 of AE, or
8/39 AE. But the distance of
the comet from the perpendicular let fall from the star A upon the right
line PE was 4/5PE.
Sunday, February 27, 8¼h. P. M. the distance of
the comet in Q from the star O was equal to the distance of the stars O
and H; and the right line QO produced passed between the stars K and B.
I could not, by reason of intervening clouds, determine the position of
the star to greater accuracy.
Tuesday, March 1, 11h . P. M. the comet in R lay
exactly in a line between the stars K and C, so as the part CR of the
right line CRK was a little greater than ⅓CK, and a little less than ⅓CK
+ 1/8CR, and therefore
= ⅓CK + 1/16CR, or
16/45CK.
Wednesday, March 2, 8h. P. M. the distance of the
comet in S from the star C was nearly 4/9FC;
the distance of the star F from the right line CS produced was 1/24FC;
and the distance of the star B from the same right line was five times
greater than the distance of the star F; and the right line NS produced
passed between the stars H and I five or six times nearer to the star H
than to the star I.
Saturday, March 5, 11½h. P. M. when the comet was
in T, the right line MT was equal to ½ML, and the right line LT produced
passed between B and F four or five times nearer to F than to B, cutting
off from BF a fifth or sixth part thereof towards F: and MT produced
passed on the outside of the space BF towards the star B four times
nearer to the star B than to the star F. M was a very small star,
scarcely to be seen by the telescope; but the star L was greater, and of
about the eighth magnitude.
Monday, March 7, 9½h. P. M. the comet being in V,
the right line Va produced did pass between B and F, cutting
off, from BF towards F, 1/10
of BF, and was to the right line Vβ as 5 to 4. And the distance
of the comet from the right line αβ was ½Vβ.
Wednesday, March 9, 8½h. P. M. the comet being in
X, the right line γX was equal to ¼γδ and the
perpendicular let fall from the star δ upon the right γX
was 2/5 of γδ.
The same night, at 12h. the comet being in Y, the right line
γY was equal to ⅓ of γδ, or
a little less, as perhaps 5/16
of γδ; and a perpendicular let fall from the star δ
on the right line γY was equal to about 1/6
or 1/7 γδ.
But the comet being then extremely near the horizon, was scarcely
discernible, and therefore its place could not be determined with that
certainty as in the foregoing observations.
Prom these observations, by constructions of figures and calculations,
I deduced the longitudes and latitudes of the comet; and Mr. Pound,
by correcting the places of the fixed stars, hath determined more
correctly the places of the comet, which correct places are set down
above. Though my micrometer was none of the best, yet the errors in
longitude and latitude (as derived from my observations) scarcely exceed
one minute. The comet (according to my observations), about the end of
its motion, began to decline sensibly towards the north, from the
parallel which it described about the end of February.
Now, in order to determine the orbit of the comet out of the
observations above described, I selected those three which Flamsted
made, Dec. 21, Jan. 5, and Jan. 25; from
which I found St of 9842,1 parts, and Vt of 455, such
as the semi-diameter of the orbis magnus contains 10000. Then
for the first observation, assuming tB of 5657 of those parts,
I found SB 9747, BE for the first time 412, Sμ 9503, iλ
413, BE for the second time 421, OD 10186, X 8528,4, PM 8450, MN 8475,
NP 25; from whence, by the second operation, I collected the distance tb
5640; and by this operation I at last deduced the distances TX 4775 and
τZ 11322. From which, limiting the orbit, I found its
descending node in ♋, and ascending node in ♑
1° 53; the inclination of its plane to the plane of the ecliptic 61°
20⅓, the vertex thereof (or the perihelion of the comet) distant from
the node 8° 38, and in ♐ 27°
43′, with latitude 7° 34′ south; its latus rectum 236,8; and
the diurnal area described by a radius drawn to the sun 93585, supposing
the square of the semi-diameter of the orbis magnus 100000000;
that the comet in this orbit moved directly according to the order of
the signs, and on Dec. 8d.00h.04′ P. M
was in the vertex or perihelion of its orbit. All which I determined by
scale and compass, and the chords of angles, taken from the table of
natural sines, in a pretty large figure, in which, to wit, the radius of
the orbis magnus (consisting of 10000 parts) was equal to 16⅓
inches of an English foot.
Lastly, in order to discover whether the comet did truly move in the
orbit so determined, I investigated its places in this orbit partly by
arithmetical operations, and partly by scale and compass, to the times
of some of the observations, as may be seen in the following table:—
| The Comet's |
|
Dist.
from
sun. |
Longitude
computed. |
Latitud.
computed. |
Longitude
observed. |
Latitude
observed |
Dif.
Lo. |
Dif.
Lat. |
Dec. 12
29
Feb. 5
Mar. 5
|
2792
8403
16669
21737
|
♑ 6°.32′
♓ 13 .13⅔
♉ 17 .00
29 .19¾
|
8°.18½
28 .00
15 .29⅔
12 . 4
|
♑ 6° 31½
♓ 13 .11
♉ 16 .597/8
29 .206/7
|
8°.26
28 .101/12
15 .272/5
12 .3½
|
+1
+2
+0
-1
|
-7½
-101/12
+ 2¼
+ ½
|
But afterwards Dr. Halley did determine the orbit to a
greater accuracy by an arithmetical calculus than could be done by
linear descriptions; and, retaining the place of the nodes in ♋ and ♑
1° 53′, and the inclination of the plane of the orbit to the ecliptic
61° 20⅓′, as well as the time of the comet's being in perihelio, Dec.
8d.00h.04′, he found the distance of the
perihelion from the ascending node measured in the comet's orbit 9° 20′,
and the lutus rectum of the parabola 2430 parts, supposing the
mean distance of the sun from the earth to be 100000 parts; and from
these data, by an accurate arithmetical calculus, he computed
the places of the comet to the times of the observations as follows:—
| The Comet's |
| True time. |
Dist from
the sun. |
Longitude
computed. |
Latitude
computed. |
Errors in
Long. Lat. |
d. h. ′ ″
Dec. 12.4.46.
21.6.37.
24.6.18.
26.5.20.
29.8. 3.
30.8.10.
Jan. 5.3.1.½
9.7. 0.
10.6. 6.
13.7. 9.
25.7.59.
30.8.22.
Feb. 2.6.35.
5.7.4.½
25.8.41.
Mar. 5.11.39.
|
28025
61076
70008
75576
84021
86661
101440
110959
113162
120000
145370
155303
160951
166686
202570
216205
|
° ′ ″
♑ 6.29.25
♒ 5.6.30
18.48.20
28.22.45
♓ 13.12.40
17.40.5
♈ 8.49.49
18.44.36
20.41.0
26.0.21
♉ 9.33.40
13.17.41
15.11.11
16.58.55
26.15.46
29.18.35
|
° ′ ″
8.26.0 bor.
21.43.20
25.22.40
27.1.36
28.10.10
28.11.20
26.15.15
24.12.54
23.44.10
22.17.30
17.57.55
16.42.7
16.4.15
15.29.13
12.48.0
15.5.40
|
′ ″
-3.5
-1.42
-1.3
-1.28
+1.59
+1.45
+0.56
+0.32
0.10
0.33
-1.20
-2.10
-2.42
-0.41
-2.49
+0.35
|
′ ″
-2.0
+1.7
-0.25
+0.44
+0.12
-0.33
+0.8
0.58
+0.18
+0.2
+1.25
-0.11
+0.14
+2.0
+1.10
+2.14
|
This comet also appeared in the November before, and at Coburg,
in Saxony, was observed by Mr. Gottfried Kirch, on
the 4th of that month, on the 6th and 11th O. S.; from its positions to
the nearest fixed stars observed with sufficient accuracy, sometimes
with a two feet, and sometimes with a ten feet telescope; from the
difference of longitudes of Coburg and London, 11°;
and from the places of the fixed stars observed by Mr. Pound,
Dr. Halley has determined the places of the comet as follows:—
Nov. 3, 17h.2′, apparent
time at London, the comet was in ♌
29 deg. 51′, with 1 deg. 17′ 45″ latitude north.
November 5. 15h.58′ the comet was in ♍ 3° 23′, with 1° 6′ nortl. lat.
November 10, 16h.31′, the comet was equally distant
from two stars in ♌ which are σ
and τ in Bayer; but it had not quite touched the
right line that joins them, but was very little distant from it. In Flamsted's
catalogue this star σ was then in ♍
14° 15′, with 1 deg. 41′ lat. north nearly, and τ in ♍ 17° 3½′, with 0 deg. 34 lat. south; and the
middle point between those stars was ♍
15° 39¼′, with 0° 33½′ lat. north. Let the distance of the comet from
that right line be about 10′ or 12′; and the difference of the longitude
of the comet and that middle point will be 7′; and the difference of the
latitude nearly 7½′; and thence it follows that the comet was in
♍ 15° 32′, with about 26′ lat. north.
The first observation from the position of the comet with respect to
certain small fixed stars had all the exactness that could be desired;
the second also was accurate enough. In the third observation, which was
the least accurate, there might be an error of 6 or 7 minutes, but
hardly greater. The longitude of the comet, as found in the first and
most accurate observation, being computed in the aforesaid parabolic
orbit, comes out ♌ 29° 30′ 22″, its
latitude north 1° 25′ 7″, and its distance from the sun 115546.
Moreover, Dr. Halley, observing that a remarkable comet had
appeared four times at equal intervals of 575 years (that is, in the
month of September after Julius Caesar was killed; An.
Chr. 531, in the consulate of Lampadius and Orestes;
An. Chr. 1106, in the month of February; and at the
end of the year 1680; and that with a long and remarkable tail, except
when it was seen after Caesar's death, at which time, by
reason of the inconvenient situation of the earth, the tail was not so
conspicuous), set himself to find out an elliptic orbit whose greater
axis should be 1382957 parts, the mean distance of the earth from the
sun containing 10000 such; in which orbit a comet might revolve in 575
years; and, placing the ascending node in ♋
2° 2′, the inclination of the plane of the orbit to the plane of the
ecliptic in an angle of 61° 6′ 48″, the perihelion of the comet in this
plane in ♐ 22° 44′ 25″, the
equal time of the perihelion December 7d.23h.9′,
the distance of the perihelion from the ascending node in the plane of
the ecliptic 9° 17′ 35″, and its conjugate axis 18481,2, he computed the
motions of the comet in this elliptic orbit. The places of the comet, as
deduced from the observations, and as arising from computation made in
this orbit, may be seen in the following table.
| True time. |
Longitudes
observed. |
Latitude
North
obs. |
Longitude
computed. |
Latitude
computed. |
Errors in
Long. Lat. |
d. h. ′
Nov. 3.16.47
5.15.37
10.16.18
16.17.00
18.21.34
20.17.0
23.17.5
Dec. 12.4.46
21.6.37
24.6.18
26.5.21
29.8.3
30.8.10
Jan. 5.6.1½
9.7.7
10.6.6
13.7.9
25.7.59
30.8.22
Feb. 2.6.35
5.7.4½
25.8.41
Mar. 1.11.10
5.11.39
9.8.38
|
° ′ ″
♌ 29.51.0
♍ 3.23.0
15.32. 0
♑ 6.32.30
♒ 5. 8.12
18.49.23
28.24.13
♓ 13.10.41
17.38. 0
♈ 8.48.53
18.44. 4
20.40.50
25.59.48
♉ 9.35. 0
13.19.51
15.13.53
16.59. 6
26.18.35
27.52.42
29.18. 0
♊ 0.43.4
|
° ′ ″
1.17.45
1.6. 0
0.27. 0
8.28. 0
21.42.13
25.23. 5
27. 0.52
28. 9.58
28.11.53
26.15. 7
24.11.56
23.43.32
22.17.28
17.56.30
16.42.18
16. 4. 1
15.27. 3
12.46.46
12.23.40
12. 3.16
11.45.52
|
° ′ ″
♌ 29.51.22
♍ 3.24.32
15.33. 2
♎ 8.16.45
18.52.15
28.10.36
♏ 13.22.42
♑ 6.31.20
♒ 5. 6.14
18.47.30
28.21.42
♓ 13.11.14
17.38.27
♈ 8.48.51
18.43.51
20.40.23
26. 0. 8
♉ 9.34.11
13.18.25
15.11.59
16.59.17
26.16.59
27.51.47
29.20.11
♊ 0.42.43
|
° ′ ″
1.17.32 N
1. 6. 9
0.25. 7
0.53. 7 S
1.26.54
1.53.35
2.29. 0
8.29. 6 N
21.44.42
25.23.35
27. 2. 1
28.10.38
28.11.37
26.14.57
24.12.17
23.43.25
22.16.32
17.56. 6
16.40. 5
16. 2.17
15.27. 0
12.45.22
12.22.28
12. 2.50
11.45.35
|
′ ″
+0.22
+1.32
+1.2
-1.10
-1.58
-1.53
-2.31
+0,33
+0.7
-0.2
-0.13
-0.27
+0.20
-0,49
-1.23
-1.54
+0.11
-1.36
-0.55
+2.11
-0.21
|
′ ″
-0.13
+0.9
-1.53
+1.6
+2.29
+0.30
+1.9
+0.40
-0.16
-0.10
+0.21
-0.7
-0.56
-0.24
-2.13
-1.54
-0.3
-1.24
-1.12
-0.26
-0.17
|
The observations of this comet from the beginning to the end agree at
perfectly with the motion of the comet in the orbit just now described
as the motions of the planets do with the theories from whence they are
calculated; and by this agreement plainly evince that it was one and the
same comet that appeared all that time, and also that the orbit of that
comet is here rightly defined.
In the foregoing table we have omitted the observations of Nov.
16, 18, 20. and 23, as not sufficiently accurate, for at those times
several persons had observed the comet. Nov. 17, O. S. Ponthaeus
and his companions, at 6h. in the morning at Rome
(that is, 5h.10′ at London], by threads directed to
the fixed stars, observed the comet in ♎
8° 30′, with latitude 0° 40 south. Their observations may be seen in a
treatise which Ponthaeus published concerning this comet. Cellius,
who was present, and communicated his observations in a letter to Cassini
saw the comet at the same hour in ♎
8° 30′, with latitude 0° 30 south. It was likewise seen by Galletius
at the same hour at Avignon (that is, at 5h.42′
morning at London) in ♎
8° without latitude. But by the theory the comet was at that time in
♎ 8° 16′ 45″, and its latitude was 0°
53′ 7″ south.
Nov. 18, at 6h.30′ in the morning at Rome
(that is, at 5h.40′ at London), Ponthaeus
observed the comet in ♎ 13° 30,
with latitude 1° 20′ south; and Cellius
in ♎ 13° 30′, with latitude 1° 00
south. But at 5h.30′ in the morning at Avignon, Galletius
saw it in ♎ 13° 00′, with latitude
1° 00 south. In the University of La Fleche, in France,
at 5h. in the morning (that is, at 5h.9 at London),
it was seen by P. Ango, in the middle between two small stars,
one of which is the middle of the three which lie in a right line in the
southern hand of Virgo, Bayers ψ; and the other is the outmost
of the wing, Bayer's θ. Whence the comet was then in ♎ 12° 46′ with latitude 50′ south. And I was
informed by Dr. Halley, that on the same day at Boston
in New England, in the latitude of 42½ deg. at 5h.
in the morning (that is, at 9h.44′ in the morning at London),
the comet was seen near ♎ 14°,
with latitude 1° 30 south.
Nov. 19, at 4½h. at Cambridge, the comet
(by the observation of a young man) was distant from Spica
♍ about 2° towards the north west. Now
the spike was at that time in ♎
19° 23′ 47″, with latitude 2° 1′ 59″ south. The same day, at 5h.
in the morning, at Boston in New England, the comet
was distant from Spica ♍ 1°, with
the difference of 40′ in latitude. The same day, in the island of Jamaica,
it was about 1° distant from Spica ♍.
The same day, Mr. Arthur Storer, at the river Patuxent,
near Hunting Creek, in Maryland, in the confines of
Virginia, in lat. 38½°, at 5 in the morning (that is, at 10h.
at London), saw the comet above Spica ♍, and very nearly joined with it, the distance
between them being about ¾ of one deg. And from these observations
compared. I conclude, that at 9h.44′ at London the
comet was in ♎ 18° 50′, with about
1° 25′ latitude south. Now by the theory the comet was at that time in
♎ 18° 52′ 15″, with 1° 26′ 54″ lat.
south.
Nov. 20, Montenari, professor of astronomy at Padua,
at 6h. in the morning at Venice (that is, 5h.10
at London), saw the comet in ♎
23°, with latitude 1° 30′ south. The same day, at Boston, it was distant
from Spica ♍ by about 4° of
longitude east, and therefore was in ♎
23° 24′ nearly.
Nov. 21, Ponthaeus and his companions, at 7¼h.
in the morning, observed the comet in ♎
27° 50′, with latitude 1° 16′ south; Cellius, in ♎ 28°; P. Ango at 5h. in the
morning, in ♎ 27° 45′; Montenari
in ♎ 27° 51′. The same day, in the
island of Jamaica, it was seen near the beginning of ♏, and of about the same latitude with Spica
♍, that is, 2° 2′. The same day, at
5h. morning, at Ballasore, in the East Indies
(that is, at 11h.20′ of the night preceding at London),
the distance of the comet from Spica ♍
was taken 7° 35′ to the east. It was in a right line between the spike
and the balance, and therefore was then in ♎
26° 58′, with about 1° 11′ lat. south; and after 5h.40′ (that
is, at 5h. morning at London), it was in ♎ 28° 12′, with 1° 16′ lat. south. Now by the
theory the comet was then in ♎ 28°
10′ 36″, with 1° 53′ 35″ lat. south.
Nov. 22, the comet was seen by Montenari in ♏ 2° 33′; but at Boston in
New England, it was found in about ♏
3°, and with almost the same latitude as before, that is, 1° 30′. The
same day, at 5h. morning at Ballasore,ihe comet was
observed in ♏ 1° 50′; and
therefore at 5h. morning at London, the comet was
♏ 3° 5′ nearly. The same day, at 6½h.
in the morning at London, Dr. Hook observed it in
about ♏ 3° 30′, and that in the
right line which passeth through Spica ♍
and Cor Leonis; not, indeed, exactly, but deviating a little
from that line towards the north. Montenari likewise observed,
that this day, and some days after, a right line drawn from the comet
through Spica passed by the south side of Cor Leonis
at a very small distance therefrom. The right line through Cor
Leonis and Spica ♍
did cut the ecliptic in ♍ 3° 46′
at an angle of 2° 51′; and if the comet had been in this line and in
♏ 3°, its latitude would have been 2°
26′; but since Hook and Montenari agree that the
comet was at some small distance from this line towards the north, its
latitude must have been something less. On the 20th, by the observation
of Montenari, its latitude was almost the same with that of Spica
♍, that is, about 1° 30′. But by
the agreement of Hook, Montenari, and Ango,
the latitude was continually increasing, and therefore must now, on the
22d, be sensibly greater than 1° 30′; and, taking a mean between the
extreme limits but now stated, 2° 26′ and 1° 30′, the latitude will be
about 1° 58′. Hook and Montenari agree that the tail
of the comet was directed towards Spica ♍,
declining a little from that star towards the south according to Hook,
but towards the north according to Montenari; and, therefore,
that declination was scarcely sensible; and the tail, lying nearly
parallel to the equator, deviated a little from the opposition of the
sun towards the north.
Nov. 23, O. S. at 5h. morning, at Nuremberg
(that is, at 4½h. at London), Mr. Zimmerman
saw the comet in ♏ 8° 8′, with
2° 31′ south lat. its place being collected by taking its distances from
fixed stars.
Nov. 24, before sun-rising, the comet was seen by Montenari
in ♏ 12° 52′ on the north side
of the right line through Cor Leonis and Spica
♍, and therefore its latitude was
something less than 2° 38′; and since the latitude, as we said, by the
concurring observations of Montenari, Ango, and Hook,
was continually increasing, therefore, it was now, on the 24th,
something greater than 1° 58′; and, taking the mean quantity, may be
reckoned 2° 18′, without any considerable error. Ponthaeus and
Galletius will have it that the latitude was now decreasing;
and Cellius, and the observer in New England, that
it continued the same, viz., of about 1°, or 1½°. The observations of Ponthaeus
and Cellius are more rude, especially those which were made by
taking the azimuths and altitudes; as are also the observations of Galletius.
Those are better which were made by taking the position of the comet to
the fixed stars by Montenari, Hook, Ango,
and the observer in New England, and sometimes by Ponthaeus
and Cellius. The same day, at 5h. morning, at Ballasore,
the comet was observed in ♏ 11°
45′; and, therefore, at 5h. morning at London, was
in ♏ 13° nearly. And, by the
theory, the comet was at that time in ♏
13° 22′ 2″.
Nov. 25, before sunrise, Montenari observed the
comet in ♏ 17¾ nearly; and Cellius
observed at the same time that the comet was in a right line between the
bright star in the right thigh of Virgo and the southern scale of Libra;
and this right line cuts the comet's way in ♏
18° 36′. And, by the theory, the comet was in ♏
18⅓° nearly.
From all this it is plain that these observations agree with the
theory, so far as they agree with one another; and by this agreement it
is made clear that it was one and the same comet that appeared all the
time from Nov. 4 to Mar. 9. The path of this comet
did twice cut the plane of the ecliptic, and therefore was not a right
line. It did cut the ecliptic not in opposite parts of the heavens, but
in the end of Virgo and beginning of Capricorn, including an arc of
about 98°; and therefore the way of the comet did very much deviate from
the path of a great circle; for in the month of Nov. it
declined at least 3° from the ecliptic towards the south; and in the
month of Dec. following it declined 29° from the ecliptic towards the
north; the two parts of the orbit in which the comet descended towards
the sun, and ascended again from the sun, declining one from the other
by an apparent angle of above 30°, as observed by Montenari.
This comet travelled over 9 signs, to wit, from the last deg. of
♌ to the beginning of ♓,
beside the sign of ♌, through which
it passed before it began to be seen; and there is no other theory by
which a comet can go over so great a part of the heavens with a regular
motion. The motion of this comet was very unequable; for about the 20th
of Nov. it described about 5° a day. Then its motion being
retarded between Nov. 26 and Dec. 12, to wit, in the space of 15½ days,
it described only 40°. But the motion thereof being afterwards
accelerated, it described near 5° a day, till its motion began to be
again retarded. And the theory which justly corresponds with a motion so
unequable, and through so great a part of the heavens, which observes
the same laws with the theory of the planets, and which accurately
agrees with accurate astronomical observations, cannot be otherwise than
true.
And, thinking it would not be improper, I have given a true
representation of the orbit which this comet described, and of the tail
which it emitted in several places, in the annexed figure; protracted in
the plane of the trajectory. In this scheme ABC represents the
trajectory of the comet, D the sun DE the axis of the trajectory, DF the
line of the nodes, GH the intersection of the sphere of the orbis
magnus with the plane of the trajectory, I the place of the comet
Nov. 4, Ann. 1680; K the place of the same Nov.
11; L the place of the same Nov. 19; M its place Dec. 12; N
 its place Dec.
21; O its place Dec. 29; P its place Jan. 5
following; Q its place Jan. 25; R its place Feb. 5;
S its place Feb. 25; T its place March 5; and V its
place March 9. In determining the length of the tail, I made
the following observations.
its place Dec.
21; O its place Dec. 29; P its place Jan. 5
following; Q its place Jan. 25; R its place Feb. 5;
S its place Feb. 25; T its place March 5; and V its
place March 9. In determining the length of the tail, I made
the following observations.
Nov. 4 and 6, the tail did not appear; Nov. 11, the
tail just begun to shew itself, but did not appear above ½ deg. long
through a 10 feet telescope; Nov. 17, the tail was seen by Ponthaeus
more than 15° long; Nov. 18, in New-England, the tail appeared
30° long, and directly opposite to the sun, extending itself to the
planet Mars, which was then in ♍,
9° 54′: Nov. 19. in Maryland, the tail was found 15°
or 20° long; Dec. 10 (by the
observation of Mr. Flamsted), the tail passed through the
middle of the distance intercepted between the tail of the Serpent of Ophiuchus
and the star δ in the south wing of Aquila, and did
terminate near the stars A, ω, b, in Bayer's tables.
Therefore the end of the tail was in ♑
19½°, with latitude about 34¼° north; Dec 11, it ascended to
the head of Sagitta (Bayer's α, β), terminating in
♑ 26° 43′, with latitude 38° 34′
north; Dec. 12, it passed through the middle of Sagitta,
nor did it reach much farther; terminating in ♒
4°, with latitude 42½° north nearly. But these things are to be
understood of the length of the brighter part of the tail; for with a
more faint light, observed, too, perhaps, in a serener sky, at Rome,
Dec. 12, 5h.40′, by the observation of Ponthaeus,
the tail arose to 10° above the rump of the Swan, and the side thereof
towards the west and towards the north was 45′ distant from this star.
But about that time the tail was 3° broad towards the upper end; and
therefore the middle thereof was 2° 15 distant from that star towards
the south, and the upper end was ♓
in 22°, with latitude 61° north; and thence the tail was about 70° long;
Dec. 21, it extended almost to Cassiopeia's chair,
equally distant from β and from Schedir, so as its
distance from either of the two was equal to the distance of the one
from the other, and therefore did terminate in ♈
24°, with latitude 47½°; Dec. 29, it reached to a contact with
Scheat on its left, and exactly filled up the space between the
two stars in the northern foot of Andromeda, being 54° in
length; and therefore terminated in ♉
19°, with 35° of latitude; Jan. 5, it touched the star π
in the breast of Andromeda on its right side, and the star μ
of the girdle on its left; and, according to our observations, was 40°
long; but it was curved, and the convex side thereof lay to the south;
and near the head of the comet it made an angle of 4° with the circle
which passed through the sun and the comet's head; but towards the other
end it was inclined to that circle in an angle of about 10° or 11°; and
the chord of the tail contained with that circle an angle of 8°. Jan.
13, the tail terminated between Alamech and Algol,
with a light that was sensible enough: but with a faint light it ended
over against the star κ in Perseus's side. The
distance of the end of the tail from the circle passing through the sun
and the comet was 3° 50′; and the inclination of the chord of the tail
to that circle was 8½°. Jan. 25 and 26. it shone with a faint
light to the length of 6° or 7°; and for a night or two after, when
there was a very clear sky, it extended to the length of 12°, or
something more, with a light that was very faint and very hardly to be
seen; but the axis thereof was exactly directed to the bright star in
the eastern shoulder of Auriga, and therefore deviated from
the opposition of the sun towards the north by an angle of 10°. Lastly,
Feb. 10, with a telescope I observed the tail 2° long; for that
fainter light which I spoke of did not appear through the glasses. But Ponthaeus
writes, that, on Feb. 7, he saw the tail 12° long. Feb.
25, the comet was without a tail, and so continued till it disappeared.
Now if one reflects upon the orbit described,
and duly considers the other appearances of this comet, he will be
easily satisfied that the bodies of comets are solid, compact, fixed,
and durable, like the bodies of the planets; for if they were nothing
else but the vapours or exhalations of the earth, of the sun, and other
planets, this comet, in its passage by the neighbourhood of the sun,
would have been immediately dissipated; for the heat of the sun is as
the density of its rays, that is, reciprocally as the square of the
distance of the places from the sun. Therefore, since on Dec.
8, when the comet was in its perihelion, the distance thereof from the
centre of the sun was to the distance of the earth from the same as
about 6 to 1000, the sun's heat on the comet was at that time to the
heat of the summer-sun with us as 1000000 to 36, or as 28000 to 1. But
the heat of boiling water is about 3 times greater than the heat which
dry earth acquires from the summer-sun, as I have tried; and the heat of
red-hot iron (if my conjecture is right) is about three or four times
greater than the heat of boiling water. And therefore the heat which dry
earth on the comet, while in its perihelion, might have conceived from
the rays of the sun, was about 2000 times greater than the heat of
red-hot iron. But by so fierce a heat, vapours and exhalations, and
every volatile matter, must have been immediately consumed and
dissipated.
This comet, therefore, must have conceived an immense heat from the
sun, and retained that heat for an exceeding long time; for a globe of
iron of an inch in diameter, exposed red-hot to the open air, will
scarcely lose all its heat in an hour's time; but a greater globe would
retain its heat longer in the proportion of its diameter, because the
surface (in proportion to which it is cooled by the contact of the
ambient air) is in that proportion less in respect of the quantity of
the included hot matter; and therefore a globe of red hot iron equal to
our earth, that is, about 40000000 feet in diameter, would scarcely cool
in an equal number of days, or in above 50000 years. But I suspect that
the duration of heat may, on account of some latent causes, increase in
a yet less proportion than that of the diameter; and I should be glad
that the true proportion was investigated by experiments.
It is farther to be observed, that the comet in the month of December,
just after it had been heated by the sun, did emit a much longer tail,
and much more splendid, than in the month of November before,
when it had not yet arrived at its perihelion; and, universally, the
greatest and most fulgent tails always arise from comets immediately
after their passing by the neighbourhood of the sun. Therefore the heat
received by the comet conduces to the greatness of the tail: from
whence, I think I may infer, that the tail is nothing else but a very
fine vapour, which the head or nucleus of the comet emits by its heat.
But we have had three several opinions about the tails of comets; for
some will have it that they are nothing else but the
beams of the sun's light transmitted through the comets heads, which
they suppose to be transparent; others, that they proceed from the
refraction which light suffers in passing from the comet's head to the
earth; and, lastly, others, that they are a sort of clouds or vapour
constantly rising from the comets heads, and tending towards the parts
opposite to the sun. The first is the opinion of such as are yet
unacquainted with optics; for the beams of the sun are seen in a
darkened room only in consequence of the light that is reflected from
them by the little particles of dust and smoke which are always flying
about in the air; and, for that reason, in air impregnated with thick
smoke, those beams appear with great brightness, and move the sense
vigorously; in a yet finer air they appear more faint, and are less
easily discerned; but in the heavens, where there is no matter to
reflect the light they can never be seen at all. Light is not seen as it
is in the beam, but as it is thence reflected to our eyes; for vision
can be no other wise produced than by rays falling upon the eyes; and,
therefore, there must be some reflecting matter in those parts where the
tails of the comets are seen: for otherwise, since all the celestial
spaces are equally illuminated by the sun's light, no part of the
heavens could appear with more splendor than another. The second opinion
is liable to many difficulties. The tails of comets are never seen
variegated with those colours which commonly are inseparable from
refraction; and the distinct transmission of the light of the fixed
stars and planets to us is a demonstration that the aether or celestial
medium is not endowed with any refractive power: for as to what is
alleged, that the fixed stars have been sometimes seen by the Egyptians
environed with a Coma or Capitlitium, because that
has but rarely happened, it is rather to be ascribed to a casual
refraction of clouds; and so the radiation and scintillation of the
fixed stars to tin refractions both of the eyes and air; for upon laying
a telescope to the eye, those radiations and scintillations immediately
disappear. By the tremulous agitation of the air and ascending vapours,
it happens that the rays of light are alternately turned aside from the
narrow space of the pupil of the eye; but no such thing can have place
in the much wider aperture of the object-glass of a telescope; and hence
it is that a scintillation is occasioned in the former case, which
ceases in the latter; and this cessation in the latter case is a
demonstration of the regular transmission of light through the heavens,
without any sensible refraction. But, to obviate an objection that may
be made from the appearing of no tail in such comets as shine but with a
faint light, as if the secondary rays were then too weak to affect the
eyes, and for that reason it is that the tails of the fixed stars do not
appear, we are to consider, that by the means of telescopes the light of
the fixed stars may be augmented above an hundred fold, and yet no tails
are seen; that the light of the planets is yet more copious without any
tail; but that comets are seen sometimes with
huge tails, when the light of their heads is but faint and dull. For so
it happened in the comet of the year 1680, when in the month of December
it was scarcely equal in light to the stars of the second magnitude, and
yet emitted a notable tail, extending to the length of 40°, 50°, 60°, or
70°, and upwards; and afterwards, on the 27th and 28th of January,
when the head appeared but us a star of the 7th magnitude, yet the tail
(as we said above), with a light that was sensible enough, though faint,
was stretched out to 6 or 7 degrees in length, and with a languishing
light that was more difficultly seen, even to 12°, and upwards. But on
the 9th and 10th of February, when to the naked eye the head
appeared no more, through a telescope I viewed the tail of 2° in length.
But farther; if the tail was owing to the refraction of the celestial
matter, and did deviate from the opposition of the sun, according to the
figure of the heavens, that deviation in the same places of the heavens
should be always directed towards the same parts. But the comet of the
year 1680, December 28d.8½h. P. M. at London,
was seen in ♓ 8° 41′, with
latitude north 28° 6′; while the sun was in ♑
18° 26′. And the comet of the year 1577, December 29d.
was in ♓ 8° 41′, with latitude
north 28° 40′, and the sun, as before, in about ♑
18° 26′. In both cases the situation of the earth was the same, and the
comet appeared in the same place of the heavens; yet in the former case
the tail of the comet (as well by my observations as by the observations
of others) deviated from the opposition of the sun towards the north by
an angle of 4½ degrees; whereas in the latter there was (according to
the observations of Tycho) a deviation of 21 degrees towards
the south. The refraction, therefore, of the heavens being thus
disproved, it remains that the phaenomena of the tails of
comets must be derived from some reflecting matter.
And that the tails of comets do arise from their heads, and tend
towards the parts opposite to the sun, is farther confirmed from the
laws which the tails observe. As that, lying in the planes of the comets
orbits which pass through the sun, they constantly deviate from the
opposition of the sun towards the parts which the comets heads in their
progress along these orbits have left. That to a spectator, placed in
those planes, they appear in the parts directly opposite to the sun;
but, as the spectator recedes from those planes, their deviation begins
to appear, and daily be comes greater. That the deviation, caeteris
paribus, appears less when the tail is more oblique to the orbit
of the comet, as well as when the head of the comet approaches nearer to
the sun, especially if the angle of deviation is estimated near the head
of the comet. That the tails which have no deviation appear straight,
but the tails which deviate are like wise bended into a certain
curvature. That this curvature is greater when the deviation is greater;
and is more sensible when the tail, caeteris paribus, is
longer; for in the shorter tails the curvature is hardly to be
perceived. That the angle of deviation is less
near the comet's head, but greater towards the other end of the tail;
and that because the convex side of the tail regards the parts from
which the deviation is made, and which lie in a right line drawn out
infinitely from the sun through the comet's head. And that the tails
that are long and broad, and shine with a stronger light, appear more
resplendent and more exactly defined on the convex than on the concave
side. Upon which accounts it is plain that the phaenomena of
the tails of comets depend upon the motions of their heads, and by no
means upon the places of the heavens in which their heads are seen; and
that, therefore, the tails of comets do not proceed from the refraction
of the heavens, but from their own heads, which furnish the matter that
forms the tail. For, as in our air, the smoke of a heated body ascends
either perpendicularly if the body is at rest, or obliquely if the body
is moved obliquely, so in the heavens, where all bodies gravitate
towards the sun, smoke and vapour must (as we have already said) ascend
from the sun, and either rise perpendicularly if the smoking body is at
rest, or obliquely if the body, in all the progress of its motion, is
always leaving those places from which the upper or higher parts of the
vapour had risen before; and that obliquity will be least where the
vapour ascends with most velocity, to wit, near the smoking body, when
that is near the sun. But, because the obliquity varies, the column of
vapour will be incurvated; and because the vapour in the preceding sides
is something more recent, that is, has ascended something more late from
the body, it will therefore be something more dense on that side, and
must on that account reflect more light, as well as be better defined. I
add nothing concerning the sudden uncertain agitation of the tails of
comets, and their irregular figures, which authors sometimes describe,
because they may arise from the mutations of our air, and the motions of
our clouds, in part obscuring those tails; or, perhaps, from parts of
the Via Lactea, which might have been confounded with and
mistaken for parts of the tails of the comets as they passed by.
But that the atmospheres of comets may furnish a supply of vapour great
enough to fill so immense spaces, we may easily understand from the
rarity of our own air; for the air near the surface of our earth
possesses a space 850 times greater than water of the same weight; and
therefore a cylinder of air 850 feet high is of equal weight with a
cylinder of water of the same breadth, and but one foot high. But a
cylinder of air reaching to the top of the atmosphere is of equal weight
with a cylinder of water about 33 feet high: and, therefore, if from the
whole cylinder of air the lower part of 850 feet high is taken away, the
remaining upper part will be of equal weight with a cylinder of water 32
feet high: and from thence (and by the hypothesis, confirmed by many
experiments, that the compression of air is as the weight of the
incumbent atmosphere, and that the force of
gravity is reciprocally as the square of the distance from the centre of
the earth) raising a calculus, by Cor. Prop. XXII, Book II, I found,
that, at the height of one semi-diameter of the earth, reckoned from the
earth's surface, the air is more rare than with us in a far greater
proportion than of the whole space within the orb of Saturn to a
spherical space of one inch in diameter; and therefore if a sphere of
our air of but one inch in thickness was equally rarefied with the air
at the height of one semi-diameter of the earth from the earth's
surface, it would fill all the regions of the planets to the orb of
Saturn, and far beyond it. Wherefore since the air at greater distances
is immensely rarefied, and the coma or atmosphere of comets is
ordinarily about ten times higher, reckoning from their centres, than
the surface of the nucleus, and the tails rise yet higher, they must
therefore be exceedingly rare; and though, on account of the much
thicker atmospheres of comets, and the great gravitation of their bodies
towards the sun, as well as of the particles of their air and vapours
mutually one towards another, it may happen that the air in the
celestial spaces and in the tails of comets is not so vastly rarefied,
yet from this computation it is plain that a very small quantity of air
and vapour is abundantly sufficient to produce all the appearances of
the tails of comets; for that they are, indeed, of a very notable rarity
appears from the shining of the stars through them. The atmosphere of
the earth, illuminated by the sun's light, though but of a few miles in
thickness, quite obscures and extinguishes the light not only of all the
stars, but even of the moon itself; whereas the smallest stars are seen
to shine through the immense thickness of the tails of comets, likewise
illuminated by the sun, without the least diminution of their splendor.
Nor is the brightness of the tails of most comets ordinarily greater
than that of our air, an inch or two in thickness, reflecting in a
darkened room the light of the sun-beams let in by a hole of the
window-shutter.
And we may pretty nearly determine the time spent during the ascent of
the vapour from the comet's head to the extremity of the tail, by
drawing a right line from the extremity of the tail to the sun, and
marking the place where that right line intersects the comet's orbit:
for the vapour that is now in the extremity of the tail, if it has
ascended in a right line from the sun, must have begun to rise from the
head at the time when the head was in the point of intersection. It is
true, the vapour does not rise in a right line from the sun, but,
retaining the motion which it had from the comet before its ascent, and
compounding that motion with its motion of ascent, arises obliquely;
and, therefore, the solution of the Problem will be more exact, if we
draw the line which intersects the orbit parallel to the length of the
tail; or rather (because of the curvilinear motion of the comet)
diverging a little from the line or length of the tail. And by means of
this principle I found that the vapour which, January 25, was
in the extremity of the tail, had begun to rise
from the head before December 11, and therefore had spent in
its whole ascent 45 days; but that the whole tail which appeared on December
10 had finished its ascent in the space of the two days then elapsed
from the time of the comet's being in its perihelion. The vapour,
therefore, about the beginning and in the neighbourhood of the sun rose
with the greatest velocity, and afterwards continued to ascend with a
motion constantly retarded by its own gravity; and the higher it
ascended, the more it added to the length of the tail; and while the
tail continued to be seen, it was made up of almost all that vapour
which had risen since the time of the comet's being in its perihelion;
nor did that part of the vapour which had risen first, and which formed
the extremity of the tail, cease to appear, till its too great distance,
as well from the sun, from which it received its light, as from our
eyes, rendered it invisible. Whence also it is that the tails of other
comets which are short do not rise from their heads with a swift and
continued motion, and soon after disappear, but are permanent and
lasting columns of vapours and exhalations, which, ascending from the
heads with a slow motion of many days, and partaking of the motion of
the heads which they had from the beginning, continue to go along
together with them through the heavens. From whence again we have
another argument proving the celestial spaces to be free, and without
resistance, since in them not only the solid bodies of the planets and
comets, but also the extremely rare vapours of comets tails, maintain
their rapid motions with great freedom, and for an exceeding long time.
Kepler ascribes the ascent of the tails of the comets to the
atmospheres of their heads; and their direction towards the parts
opposite to the sun to the action of the rays of light carrying along
with them the matter of the comets tails; and without any great
incongruity we may suppose, that, in so free spaces, so fine a matter as
that of the aether may yield to the action of the rays of the sun's
light, though those rays are not able sensibly to move the gross
substances in our parts, which are clogged with so palpable a
resistance. Another author thinks that there may be a sort of particles
of matter endowed with a principle of levity, as well as others are with
a power of gravity; that the matter of the tails of comets may be of the
former sort, and that its ascent from the sun may be owing to its
levity; but, considering that the gravity of terrestrial bodies is as
the matter of the bodies, and therefore can be neither more nor less in
the same quantity of matter, I am inclined to believe that this ascent
may rather proceed from the rarefaction of the matter of the comets
tails. The ascent of smoke in a chimney is owing to the impulse of the
air with which it is entangled. The air rarefied by heat ascends,
because its specific gravity is diminished, and in its ascent carries
along with it the smoke with which it is engaged; and why may not the
tail of a comet rise from the sun after the same manner? For
the sun's rays do not act upon the mediums which they pervade otherwise
than by reflection and refraction; and those reflecting particles heated
by this action, heat the matter of the aether which is involved with
them. That matter is rarefied by the heat which it acquires, and be
cause, by this rarefaction, the specific gravity with which it tended
towards the sun before is diminished, it will ascend therefrom, and
carry along with it the reflecting particles of which the tail of the
comet is composed. But the ascent of the vapours is further promoted by
their circumgyration about the sun, in consequence whereof they
endeavour to recede from the sun, while the sun's atmosphere and the
other matter of the heavens are either altogether quiescent, or are only
moved with a slower circumgyration derived from the rotation of the sun.
And these are the causes of the ascent of the tails of the comets in the
neighbourhood of the sun, where their orbits are bent into a greater
curvature, and the comets themselves are plunged into the denser and
therefore heavier parts of the sun's atmosphere: upon which account they
do then emit tails of an huge length; for the tails which then arise,
retaining their own proper motion, and in the mean time gravitating
towards the sun, must be revolved in ellipses about the sun in like
manner as the heads are, and by that motion must always accompany the
heads, and freely adhere to them. For the gravitation of the vapours
towards the sun can no more force the tails to abandon the heads, and
descend to the sun, than the gravitation of the heads can oblige them to
fall from the tails. They must by their common gravity either fall
together towards the sun, or be retarded together in their common ascent
therefrom; and, therefore (whether from the causes already described, or
from any others), the tails and heads of comets may easily acquire and
freely retain any position one to the other, without disturbance or
impediment from that common gravitation.
The tails, therefore, that rise in the perihelion positions of the
comets will go along with their heads into far remote parts, and
together with the heads will either return again from thence to us,
after a long course of years, or rather will be there rarefied, and by
degrees quite vanish away; for afterwards, in the descent of the heads
towards the sun, new short tails will be emitted from the heads with a
slow motion; and those tails by degrees will be augmented immensely,
especially in such comets as in their perihelion distances descend as
low as the sun's atmosphere; for all vapour in those free spaces is in a
perpetual state of rarefaction and dilatation; and from hence it is that
the tails of all comets are broader at their upper extremity than near
their heads. And it is not unlikely but that the vapour, thus
perpetually rarefied and dilated, may be at last dissipated and
scattered through the whole heavens, and by little and little be
attracted towards the planets by its gravity, and mixed with their
atmosphere; for as the seas are absolutely necessary to the constitution
of our earth, that from them, the sun, by its
heat, may exhale a sufficient quantity of vapours, which, being gathered
together into clouds, may drop down in rain, for watering of the earth,
and for the production and nourishment of vegetables; or, being
condensed with cold on the tops of mountains (as some philosophers with
reason judge), may run down in springs and rivers; so for the
conservation of the seas, and fluids of the planets, comets seem to be
required, that, from their exhalations and vapours condensed, the wastes
of the planetary fluids spent upon vegetation and putrefaction, and
converted into dry earth, may be continually supplied and made up; for
all vegetables entirely derive their growths from fluids, and
afterwards, in great measure, are turned into dry earth by putrefaction;
and a sort of slime is always found to settle at the bottom of putrefied
fluids; and hence it is that the bulk of the solid earth is continually
increased; and the fluids, if they are not supplied from without, must
be in a continual decrease, and quite fail at last. I suspect, moreover,
that it is chiefly from the comets that spirit comes, which is indeed
the smallest but the most subtle and useful part of our air, and so much
required to sustain the life of all things with us.
The atmospheres of comets, in their descent towards the sun, by running
out into the tails, are spent and diminished, and become narrower, at
least on that side which regards the sun; and in receding from the sun,
when they less run out into the tails, they are again enlarged, if Hevelius
has justly marked their appearances. But they are seen least of all just
after they have been most heated by the sun, and on that account then
emit the longest and most resplendent tails; and, perhaps, at the same
time, the nuclei are environed with a denser and blacker smoke in the
lowermost parts of their atmosphere; for smoke that is raised by a great
and intense heat is commonly the denser and blacker. Thus the head of
that comet which we have been describing, at equal distances both from
the sun and from the earth, appeared darker after it had passed by its
perihelion than it did before; for in the month of December it
was commonly compared with the stars of the third magnitude, but in November
with those of the first or second; and such as saw both appearances have
described the first as of another and greater comet than the second.
For, November 19, this comet appeared to a young man at Cambridge,
though with a pale and dull light, yet equal to Spica Virginis;
and at that time it shone with greater brightness than it did
afterwards. And Montenari, November 20, st. vet.
observed it larger than the stars of the first magnitude, its tail being
then 2 degrees long. And Mr. Storer (by letters which have
come into my hands) writes, that in the month of December,
when the tail appeared of the greatest bulk and splendor, the head was
but small, and far less than that which was seen in the month of November
before sun-rising; and, conjecturing at the cause of the appearance, he
judged it to proceed from there being a greater
quantity of matter in the head at first, which was afterwards gradually
spent.
And, which farther makes for the same purpose, I find, that the heads
of other comets, which did put forth tails of the greatest bulk and
splendor, have appeared but obscure and small. For in Brazil, March
5, 1668, 7h. P. M., St. N. P. Valentinus Estancius
saw a comet near the horizon, and towards the south west, with a head so
small as scarcely to be discerned, but with a tail above measure
splendid, so that the reflection thereof from the sea was easily seen by
those who stood upon the shore; and it looked like a fiery beam extended
23° in length from the west to south, almost parallel to the horizon.
But this excessive splendor continued only three days, decreasing apace
afterwards; and while the splendor was decreasing, the bulk of the tail
increased: whence in Portugal it is said to have taken up one
quarter of the heavens, that is, 45 degrees, extending from west to east
with a very notable splendor, though the whole tail was not seen in
chose parts, because the head was always hid under the horizon: and from
the increase of the bulk and decrease of the splendor of the tail, it
appears that the head was then in its recess from the sun, and had been
very near to it in its perihelion, as the comet of 1680 was. And we
read, in the Saxon Chronicle, of a like comet appearing in the
year 1106, the star whereof was small and obscure (as that of
1680), but the splendour of its tail was very bright, and like a
huge fiery beam stretched out in a direction between the east and
north, as Hevelius has it also from Simeon,
the monk of Durham. This comet appeared in the beginning of February,
about the evening, and towards the south west part of heaven; from
whence, and from the position of the tail, we infer that the head was
near the sun. Matthew Paris says, It was distant from the
sun by about a cubit, from, three of the clock (rather six) till
nine, putting forth a long tail. Such also was that most
resplendent comet described by Aristotle, lib. 1, Meteor.
6. The head whereof could not be seen, because it had set before
the sun, or at least was hid under the sun's rays; but next day it was
seen as well as might be; for, having left the sun but a very little
way, it set immediately after it. And the scattered light of the
head,, obscured by the too great splendour (of the tail) did
not yet appear. But afterwards (as Aristotle says) when
the splendour (of the tail) was now diminished (the
head of), the comet recovered its native brightness; and the
splendour (of its tail) reached now to a third part of the
heavens (that is, to 60°). This appearance was in the winter
season (an. 4, Olymp. 101), and, rising to Orion's girdle,
it there vanished away.
It is true that the comet of 1618, which
came out directly from under the sun's rays with a very large tail,
seemed to equal, if not to exceed, the stars of the first magnitude;
but, then, abundance of other comets have appeared yet greater than
this, that put forth shorter tails; some of which are said to
have appeared as big as Jupiter, others as big as Venus, or even as the
moon.
We have said, that comets are a sort of planets revolved in very
eccentric orbits about the sun; and as, in the planets which are without
tails, those are commonly less which are revolved in lesser orbits, and
nearer to the sun, so in comets it is probable that those which in their
perihelion approach nearer to the sun ate generally of less magnitude,
that they may not agitate the sun too much by their attractions. But as
to the transverse diameters of their orbits, and the periodic times of
their revolutions, I leave them to be determined by comparing comets
together which after long intervals of time return again in the same
orbit. In the mean time, the following Proposition may give some light
in that inquiry.
Operation 1. Assume that position of the plane
of the trajectory which was determined according to the preceding
proposition; and select three places of the comet, deduced from very
accurate observations, and at great distances one from the other. Then
suppose A to represent the time between the first observation and the
second, and B the time between the second and the third; but it will be
convenient that in one of those times the comet be in its perigeon, or
at least not far from it. From those apparent places find, by
trigonometric operations, the three true places of the comet in that
assumed plane of the trajectory; then through the places found, and
about the centre of the sun as the focus, describe a conic section by
arithmetical operations, according to Prop. XXI., Book 1. Let the areas
of this figure which are terminated by radii drawn from the sun to the
places found be D and E; to wit, D the area between the first
observation and the second, and E the area between the second and third;
and let T represent the whole time in which the whole area D + E should
be described with the velocity of the comet found by Prop. XVI., Book 1.
Oper. 2. Retaining the inclination of the plane
of the trajectory to the plane of the ecliptic, let the longitude of the
nodes of the plane of the trajectory be increased by the addition of 20
or 30 minutes, which call P. Then from the aforesaid three observed
places of the comet let the three true places be found (as before) in
this new plane; as also the orbit passing through those places, and the
two areas of the same described between the two observations, which call
d and e; and let t be the whole time in
which the whole area d + e should be described.
Oper. 3. Retaining the longitude of the nodes
in the first operation, let the inclination of the plane of the
trajectory to the plane of the ecliptic be increased by adding thereto
20′ or 30′, which call Q. Then from the aforesaid
three observed apparent places of the comet let the three true places be
found in this new plane, as well as the orbit passing through them, and
the two areas of the same described between the observation, which call
δ and ε; and let τ be the whole time in
which the whole area δ + ε should be described.
Then taking C to 1 as A to B; and G to 1 as D to E; and g to
1 as d to e; and γ to 1 as δ to
ε; let S be the true time between the first observation and the
third; and, observing well the signs + and −, let such numbers m
and n be found out as will make 2G − 2C, =
mG − mg + nG − nγ; and
2T − 2S = mT − mt + nT − nτ.
And if, in the first operation, I represents the inclination of the
plane of the trajectory to the plane of the ecliptic, and K the
longitude of either node, then I + nQ will be the true
inclination of the plane of the trajectory to the plane of the ecliptic,
and K + mP the true longitude of the node. And, lastly, if in
the first, second, and third operations, the quantities R, r,
and ρ, represent the parameters of the trajectory, and the
quantities 1⁄L,
1⁄l, 1⁄λ,
the transverse diameters of the same, then R + mr
− mR + nρ − nR will be the true
parameter, and 1
L + ml − mL + nλ − nL
will be the true transverse diameter of the trajectory which the comet
describes; and from the transverse diameter given the periodic time of
the comet is also given. Q.E.I. But the periodic
times of the revolutions of comets, and the transverse diameters of
their orbits, cannot be accurately enough determined but by comparing
comets together which appear at different times. If, after equal
intervals of time, several comets are found to have described the same
orbit, we may thence conclude that they are all but one and the same
comet revolved in the same orbit; and then from the times of their
revolutions the transverse diameters of their orbits will be given, and
from those diameters the elliptic orbits themselves will be determined.
To this purpose the trajectories of many comets ought to be computed,
supposing those trajectories to be parabolic; for such trajectories will
always nearly agree with the phaenomena, as appears not only
from the parabolic trajectory of the comet of the year 1680, which I
compared above with the observations, but likewise from that of the
notable comet which appeared in the year 1664 and 1665, and was observed
by Hevelius, who, from his own observations, calculated the
longitudes and latitudes thereof, though with little accuracy. But from
the same observations Dr. Halley did again compute its places;
and from those new places determined its trajectory, finding its
ascending node in ♊ 21° 13′ 55″;
the inclination of the orbit to the plane of the ecliptic 21° 18′ 40″;
the distance of its perihelion from the node, estimated in the comet's
orbit, 49° 27′ 30°, its perihelion in ♌
8° 40′ 30″, with heliocentric latitude south 16°
01′ 45″; the comet to have been in its perihelion November 24d.1h.52′
P.M. equal time at London, or 13h.8′ at Dantzick,
O. S.; and that the latus rectum of the parabola was 410286
such parts as the sun's mean distance from the earth is supposed to
contain 100000. And how nearly the places of the comet computed in this
orbit agree with the observations, will appear from the annexed table,
calculated by Dr. Halley.
Appar. Time
at Dantzick. |
The observed Distances of the Comet from |
The observed Places. |
The Places
computed in
the orb. |
December
d. h. ′
3.18.29½
|
The Lion's heart
The Virgin's spike
|
° ′ ″
46.24.20
22.52.10
|
Long. ♎
Lat. S.
|
° ′ ″
7.01.00
21.39.0
|
♎ |
° ′ ″
7.1.29
21.38.50
|
| 4.18.1½ |
The Lion's heart
The Virgin's spike |
46.2.45
23.52.40
|
Long. ♎
Lat. S.
|
6.15.0
22.24.0
|
♎ |
6.16.5
22.24.0
|
|
7.17.48 |
The Lion's heart
The Virgin's spike
|
44.48.0
27.53.40
|
Long. ♎
Lat. S.
|
3.6.0
25.22.0
|
♎ |
3.7.33
25.21.40
|
| 7.17.48 |
The Lion's heart
Orion's right shoulder
|
53.15.15
45.43.30
|
Long. ♌
Lat. S.
|
2.56.0
49.25.0
|
♌ |
2.56.0
49.25.0
|
| 19.9.25 |
Procyon
Bright star of Whale's jaw
|
35.13.50
52.56.0
|
Long. ♊
Lat. S.
|
28.40.30
45.48.0
|
♊ |
28.43.0
45.46.0
|
| 20.9.53½ |
Procyon
Bright star of Whale's jaw
|
40.49.0
40.04.0
|
Long. ♊
Lat. S.
|
13.03.0
39.54.0
|
♊ |
13.5.0
39.5.0
|
| 21.9.9½ |
Orion's right shoulder
Bright star of Whale's jaw
|
26.21.25
29.28.0
|
Long. ♊
Lat. S.
|
2.16.0
33.41.0
|
♊ |
2.18.30
33.39.40
|
| 22.9.0 |
Orion's right shoulder
Bright star of Whale's jaw
|
29.47.0
20.29.30
|
Long. ♉
Lat. S.
|
24.24.0
27.45.0
|
♉ |
24.27.0
27.46.0
|
| 26.7.58 |
The bright star of Aries
Aldebaran
|
20.20.0
26.44.0
|
Long. ♉
Lat. S.
|
9.0.0
12.36.0
|
♉ |
9.2.28
12.34.13
|
| 27.6.45 |
The bright star of Aries
Aldebaran
|
20.45.0
28.10.0
|
Long. ♉
Lat. S.
|
7.5.40
10.23.0
|
♉ |
7.8.45
10.23.13
|
| 28.7.39 |
The bright star of Aries
Palilicium
|
18.29.0
29.37.0
|
Long. ♉
Lat. S.
|
5.24.45
8.22.50
|
♉ |
5.27.52
8.23.37
|
| 31.6.45 |
Andromeda's girdle
Palilicium
|
30.48.10
32.53.30
|
Long. ♉
Lat. S.
|
2.7.40
4.13.0
|
♉ |
2.8.20
4.16.25
|
Jan. 1665
7.7.37½
|
Andromeda's girdle
Palilicium
|
25.11.0
37.12.25
|
Long. ♈
Lat. N.
|
28.24.47
0.54.0
|
♈ |
28.24.0
0.53.0
|
| 13.7.0 |
Andromeda's head
Palilicium
|
28.7.10
38.55.20
|
Long. ♈
Lat. N.
|
27.6.54
3.6.50
|
♈ |
27.6.39
3.7.40
|
| 24.7.29 |
Andromeda's girdle
Palilicium
|
20.32.15
40.5.0
|
Long. ♈
Lat. N.
|
26.29.15
5.25.50
|
♈ |
26.28.50
5.26.0
|
Feb.
7.8.37 |
|
|
Long. ♈
Lat. N. |
27.4.46
7.3.29 |
♈ |
27.24.55
7.3.15 |
| 22.8.46 |
|
|
Long. ♈
Lat. N. |
28.29.46
8.12.36 |
♈ |
28.29.58
8.10.25 |
March
1.8.16 |
|
|
Long. ♈
Lat. N. |
29.18.15
8.36.26 |
♈ |
29.18.20
8.36.12 |
| 7.8.37 |
|
|
Long. ♉
Lat. N. |
0.2.48
8.56.30 |
♉ |
0.2.42
8.56.56 |
In February, the beginning of the year 1665, the first star
of Aries, which I shall hereafter call γ, was in
♈ 28° 30′ 15″, with 7° 8′ 58″ north lat.;
the second star of Aries was in ♈
29° 17′ 18″, with 8° 28′ 16″ north lat.; and another star of the seventh
magnitude, which I call A, was in ♈
28° 24′ 45″, with 8° 28′ 33″ north lat. The comet Feb. 7d.7h.30′
at Paris (that is, Feb. 7d.8h.30′
at Dantzick) O. S. made a triangle with those stars γ and A,
which was right-angled in γ; and the distance of the comet
from the star γ was equal to the distance of the stars γ
and A, that is, 1° 19′ 46″ of a great circle; and therefore in the
parallel of the latitude of the star γ it was 1° 20′ 26″.
Therefore if from the longitude of the star γ there be
subducted the longitude 1° 20′ 26″, there will remain the longitude of
the comet ♈ 27° 9′ 49″. M. Auzout,
from this observation of his, placed the comet in ♈
27° 0′, nearly; and, by the scheme in which Dr. Hooke
delineated its motion, it was then in ♈
26° 59′ 24″. I place it in ♈ 27°
4′ 46″, taking the middle between the two extremes.
From the same observations, M. Auzout made the latitude of
the comet at that time 7° and 4′ or 5′ to the north; but he had done
better to have made it 7° 3′ 29″, the difference of the latitudes of the
comet and the star γ being equal to the difference of the
longitude of the stars γ and A.
February 22d.7h.30′ at London,
that is, February 22d. 8h.46′ at Dantzick,
the distance of the comet from the star A, according to Dr. Hooke's
observation, as was delineated by himself in a scheme, and also by the
observations of M. Auzout, delineated in like manner by M. Petit,
was a fifth part of the distance between the star A and the first star
of Aries, or 15′ 57″; and the distance of the comet from a right line
joining the star A and the first of Aries was a fourth part of the same
fifth part, that is, 4′; and therefore the comet was in ♈ 28° 29′ 46″, with 8° 12′ 36″ north lat.
March 1, 7h at London, that is, March
1, 8h.16′ at Dantzick. the comet was observed near
the second star in Aries, the distance between them being to the
distance between the first and second stars in Aries, that is, to 1°
33′, as 4 to 45 according to Dr. Hooke, or as 2 to 23 according to M. Gottignies.
And, therefore, the distance of the comet from the second star in Aries
was 8′ 16″ according to Dr. Hooke, or 8′ 5″ according to M. Gottignies;
or, taking a mean between both, 8′ 10″. But, according to M. Gottignies,
the comet had gone beyond the second star of Aries about a fourth or a
fifth part of the space that it commonly went over in a day, to wit,
about 1′ 35″ (in which he agrees very well with M. Auzout);
or, according to Dr. Hooke, not quite so much, as perhaps only
1′. Wherefore if to the longitude of the first star in Aries we add 1′,
and 8′ 10″ to its latitude, we shall have the longitude of the comet
♈ 29° 18′, with 8° 36′ 26″ north lat.
March 7, 7h.30′ at Paris (that is, March
7, 8h.37′ at Dantzick), from the observations of M.
Auzout, the distance of the comet from the second star in Aries
was equal to the distance of that star from the star A,
that is, 52.′29″; and the difference of the longitude of the comet and
the second star in Aries was 45′ or 46′, or, taking a mean quantity, 45′
30″; and therefore the comet was in ♉
0° 2′ 48″. From the scheme of the observations of M. Auzout,
constructed by M. Petit, Hevelius collected the latitude of
the comet 8° 54′. But the engraver did not rightly trace the curvature
of the comet's way towards the end of the motion; and Hevelius,
in the scheme of M. Auzout's observations which he constructed
himself, corrected this irregular curvature, and so made the latitude of
the comet 8° 55′ 30″. And, by farther correcting this irregularity, the
latitude may become 8° 56, or 8° 57′.
This comet was also seen March 9, and at that time its place
must have been in ♉ 0° 18′, with
9° 3½′ north lat. nearly.
This comet appeared three months together, in which space of time it
travelled over almost six signs, and in one of the days thereof
described almost 20 deg. Its course did very much deviate from a great
circle, bending towards the north, and its motion towards the end from
retrograde became direct; and, notwithstanding its course was so
uncommon, yet by the table it appears that the theory, from beginning to
end, agrees with the observations no less accurately than the theories
of the planets usually do with the observations of them: but we are to
subduct about 2′ when the comet was swiftest, which we may effect by
taking off 12″ from the angle between the ascending node and the
perihelion, or by making that angle 49° 27′ 18″. The annual parallax of
both these comets (this and the preceding) was very conspicuous, and by
its quantity demonstrates the annual motion of the earth in the orbis
magnus.
This theory is likewise confirmed by the motion of that comet, which in
the year 1683 appeared retrograde, in an orbit whose plane contained
almost a right angle with the plane of the ecliptic, and whose ascending
node (by the computation of Dr. Halley) was in
♍ 23° 23′; the inclination of its orbit to the
ecliptic 83° 11′; its perihelion in ♊
25° 29′ 30″; its perihelion distance from the sun 56020 of such parts as
the radius of the orbis magnus contains 100000; and the time
of its perihelion July 2d.3h.50′. And
the places thereof, computed by Dr. Halley in this orbit, are
compared with the places of the same observed by Mr. Flamsted,
in the following table:—
1683
Eq. time. |
sun's place |
Comet's
Long. com. |
Lat. Nor.
comput. |
Comet's
Long. obs'd |
Lat.Nor.
observ'd |
Diff.
Long. |
Diff.
Lat. |
d. h. ′
July 13.12.55
15.11.15
17.10.20
23.13.40
25.14.5
31.9.42
31.14.55
Aug. 2.14.56
4.10.49
6.10.9
9.10.26
15.14.1
16.15.10
18.15.44
22.14.44
23.15.52
26.16. 2
|
° ′ ″
♌ 1.02.30
2.53.12
4.45.45
10.38.21
12.35.28
18.09.22
18.21.53
20.17.16
22.02.50
23.56.45
26.50.52
♍ 2.47.13
3.48. 2
5.45.33
9.35.49
10.36.48
13.31.10
|
° ′ ″
♋ 13.05.42
11.37.48
10. 7. 6
5.10.27
3.27.53
♊ 27.55. 3
27.41. 7
25.29.32
23.18.20
20.42.23
16 7.57
3.30.48
0.43. 7
♉ 24.52.53
11. 7.14
7. 2.18
♈ 24.45.31
|
° ′ ″
29.28.13
29.34. 0
29.33.30
28.51.42
24.24.47
26.22.52
26.16.57
25.16.19
24.10.49
22.17. 5
20. 6.37
11.37.33
9.34.16
5.11.15
South.
5.16.58
8.17. 9
16.38. 0
|
° ′ ″
♋ 13. 6.42
11.39.43
10. 8.40
5.11.30
3.27. 0
♊ 27.54.24
27.41. 8
25.28.46
23.16.55
20.40.32
16. 5.55
3.26.18
0.41.55
♉ 24.49. 5
11.07.12
7. 1.17
♈ 24.44.00
|
° ′ ″
29.28.20
29.34.50
29.34. 0
28.50.28
28.23.40
26.22.25
26.14.50
25.17.28
24.12.19
22.49. 5
20. 6.10
11.32. 1
9.34.13
5. 9.11
South
5.16.58
8.16.41
16.38.20
|
′ ″
+ 1.00
+ 1.55
+ 1.34
+ 1.03
- 0.53
- 0.39
+ 0. 1
- 0.46
- 1.25
- 1.51
- 2. 2
- 4.30
- 1.12
- 3.48
- 0. 2
- 1. 1
- 1.31
|
′ ″
+ 0.07
+ 0.50
+ 0.30
- 1.14
-1. 7
- 0.27
- 2. 7
+ 1. 9
+ 1.30
+ 2. 0
- 0.27
- 5.32
- 0. 3
- 2. 4
-0. 3
- 0.28
+ 0.20
|
This theory is yet farther confirmed by the motion of that retrograde
comet which appeared in the year 1682. The ascending node of this (by
Dr. Halley's computation) was in ♉
21° 16′ 30″; the inclination of its orbit to the plane of the ecliptic
17° 56′ 00″; its perihelion in ♒
2° 52′ 50″; its perihelion distance from the sun 58328 parts, of which
the radius of the orbis magnus contains 100000; the equal time
of the comet's being in its perihelion Sept. 4d.7h.39′.
And its places, collected from Mr. Flamsted's observations,
are compared with its places computed from our theory in the following
table:—
1682
App. Time. |
sun's place |
Comet's
Long. comp. |
Lat. Nor.
comp. |
Com. Long.
observed. |
Lat.Nor.
observ. |
Diff.
Long. |
Diff.
Lat. |
d. h. ′
Aug. 19.16.38
20.15.38
21. 8.21
22. 8. 8
29.08.20
30. 7.45
Sept. 1. 7.33
4. 7.22
5. 7.32
8. 7.16
9. 7.26
|
° ′ ″
♍ 7. 0. 7
7.55 52
8.36.14
9.33.55
16.22.40
17.19.41
19.16. 9
22.11.28
23.10.29
26. 5.58
27. 5. 9
|
° ′ ″
♌ 18.14 28
24.46.23
29.37.15
♍ 6.29.53
♎ 12.37.54
15 36. 1
20.30.53
25.42. 0
27. 0.46
29.58.44
♏ 0.44.10
|
° ′ ″
25.50. 7
26.14.42
26.20. 3
26. 8.42
18.37.47
17.26.43
15.13. 0
12.23.48
11.33.08
9.26.46
8.49.10
|
° ′ ″
♌ 18.14.40
24.46.22
29.38.02
♍ 6.30. 3
♎ 12.37.49
15.35.18
20.27. 4
25.40.58
26.59.24
29.58.45
♏ 0.44. 4
|
° ′ ″
25.49.55
26.12.52
26.17.37
26. 7.12
18.34. 5
17.27.17
15. 9.49
12.22. 0
11.33.51
9.26.43
8.48.25
|
′ ″
- 0.12
+ 0. 1
- 0.47
- 0.10
+ 0. 5
+ 0.43
+ 3.49
+ 1. 2
+ 1.22
- 0.1
+ 0. 6
|
′ ″
+ 0.12
+ 1.50
+ 2.26
+ 1.30
+ 3.42
- 0.34
+ 3.11
+ 1.48
- 0.43
+ 0. 3
+ 0.45
|
This theory is also confirmed by the retrograde motion of the comet
that appeared in the year 1723. The ascending node of this comet
(according to the computation of Mr. Bradley, Savilian
Professor of Astronomy at Oxford) was in ♈
14° 16′. The inclination of the orbit to the plane of the ecliptic 49°
59′. Its perihelion was in ♉ 12°
15′ 20″. Its perihelion distance from the sun 998651 parts, of which the
radius of the orbis magnus contains 1000000, and the equal
time of its perihelion September 16d 16h.10′.
The places of this comet computed in this orbit by Mr. Bradley,
and compared with the places observed by himself, his uncle Mr. Pound,
and Dr. Halley, may be seen in the following table.
1723
Eq. Time. |
Comet's
Long. obs. |
Lat. Nor.
obs. |
Comet's
Lon. com. |
Lat.Nor.
comp. |
Diff.
Lon. |
Diff.
Lat. |
d. h. ′
Oct. 9.8. 5
10.6.21
12.7.22
14.8.57
15.6.35
21.6.22
22. 6.24
24.8. 2
29.8.56
30.6.20
Nov. 5.5.53
8.7. 6
14.6.20
20.7.45
Dec. 7.6.45
|
° ′ ″
♒ 7.22.15
6.41.12
5.39.58
4.59.49
4.47.41
4. 2.32
3.59. 2
3.55.29
3.56.17
3.58. 9
4.16.30
4.29.36
5. 2.16
5.42.20
8. 4.13
|
° ′ ″
5. 2. 0
7.44.13
11.55. 0
14.43.50
15.40.51
19.41.49
20. 8.12
20.55.18
22.20.27
22.32.28
23.38 33
24. 4.30
24.48.46
25.24.45
26.54.18
|
° ′ ″
♒7.21.26
6.41.42
5.40.19
5. 0.37
4.47.45
4. 2.21
3.59.10
3.55.11
3.56.42
3.58.17
4.16.23
4.29.54
5. 2.51
5.43.13
8. 3.55
|
° ′ ″
5. 2 47
7.43.18
11.54.55
14.44. 1
15.40.55
19.42. 3
20. 8.17
20.55. 9
22.20.10
22.32.12
23.38. 7
24. 4.40
24.48.16
25.25.17
26.53.42
|
″
+ 49
- 50
- 21
- 48
- 4
+ 11
- 8
+ 18
- 25
- 8
+ 7
- 18
- 35
- 53
+ 18
|
″
- 47
+ 55
+ 5
- 11
- 4
- 14
- 5
+ 9
+ 17
+ 16
+ 26
- 10
+ 30
- 32
+ 36
|
From these examples it is abundantly evident that the motions of comets
are no less accurately represented by our theory than the motions of the
planets commonly are by the theories of them; and, therefore, by means
of this theory, we may enumerate the orbits of comets, and so discover
the periodic time of a comet's revolution in any orbit; whence, at last,
we shall have the transverse diameters of their elliptic orbits and
their aphelion distances.
That retrograde comet which appeared in the year 1607 described an
orbit whose ascending node (according to Dr. Halley's
computation) was in ♉ 20° 21′;
and the inclination of the plane of the orbit to the plane of the
ecliptic 17° 2′; whose perihelion was in ♒
2° 16′; and its perihelion distance from the sun 58680 of such parts as
the radius of the orbis magnus contains 100000; and the comet
was in its perihelion October 16d.3h.50′;
which orbit agrees very nearly with the orbit of the comet which was
seen in 1682. If these were not two different comets, but one and the
same, that comet will finish one revolution in the space of 75 years;
and the greater axis of its orbit will be to the greater axis of the orbis
magnus as ∛752 to 1, or as
1778 to 100, nearly. And the aphelion distance of this comet from the
sun will be to the mean distance of the earth from the sun as about 35
to 1; from which data it will be no hard matter to determine the
elliptic orbit of this comet. But these things are to be supposed on
condition, that, after the space of 75 years, the same comet shall
return again in the same orbit. The other comets seem to ascend to
greater heights, and to require a longer time to perform their
revolutions.
But, because of the great number of comets, of the great distance of
their aphelions from the sun, and of the
slowness of their motions in the aphelions, they will, by their mutual
gravitations, disturb each other; so that their eccentricities and the
times of their revolutions will be sometimes a little increased, and
sometimes diminished. Therefore we are not to expect that the same comet
will return exactly in the same orbit, and in the same periodic times:
it will be sufficient if we find the changes no greater than may arise
from the causes just spoken of.
And hence a reason may be assigned why comets are not comprehended
within the limits of a zodiac, as the planets are; but, being confined
to no bounds, are with various motions dispersed all over the heavens;
namely, to this purpose, that in their aphelions, where their motions
are exceedingly slow, receding to greater distances one from another,
they may suffer less disturbance from their mutual gravitations: and
hence it is that the comets which descend the lowest, and therefore move
the slowest in their aphelions, ought also to ascend the highest.
The comet which appeared in the year 1680 was in its perihelion less
distant from the sun than by a sixth part of the sun's diameter; and
because of its extreme velocity in that proximity to the sun, and some
density of the sun's atmosphere, it must have suffered some resistance
and retardation; and therefore, being attracted something nearer to the
sun in every revolution, will at last fall down upon the body of the
sun. Nay, in its aphelion, where it moves the slowest, it may sometimes
happen to be yet farther retarded by the attractions of other comets,
and in consequence of this retardation descend to the sun. So fixed
stars, that have been gradually wasted by the light and vapours emitted
from them for a long time, may be recruited by comets that fall upon
them; and from this fresh supply of new fuel those old stars, acquiring
new splendor, may pass for new stars. Of this kind are such fixed stars
as appear on a sudden, and shine with a wonderful brightness at first,
and afterwards vanish by little and little. Such was that star which
appeared in Cassiopeia's chair; which Cornelius Gemma
did not see upon the 8th of November, 1572, though he was
observing that part of the heavens upon that very night, and the sky was
perfectly serene; but the next night (November 9) he saw it
shining much brighter than any of the fixed stars, and scarcely inferior
to Venus in splendor. Tycho Brahe saw it upon the
11th of the same month, when it shone with the greatest lustre; and from
that time he observed it to decay by little and little; and in 16
months' time it entirely disappeared. In the month of November,
when it first appeared, its light was equal to that of Venus.
In the month of December its light was a little diminished,
and was now become equal to that of Jupiter. In January 1573
it was less than Jupiter, and greater than Sirius;
and about the end of February and the beginning of March
became equal to that star. In the months of April and May
it was equal to a star of the second magnitude; in
June, July, and August, to a star of the third
magnitude; in September, October, and November, to
those of the fourth magnitude; in December and January
1574 to those of the fifth; in February to those of the sixth
magnitude; and in March it entirely vanished. Its colour at
the beginning was clear, bright, and inclining to white; afterwards it
turned a little yellow; and in March 1573 it became ruddy,
like Mars or Aldebaran: in May it turned
to a kind of dusky whiteness, like that we observe in Saturn;
and that colour it retained ever after, but growing always more and more
obscure. Such also was the star in the right foot of Serpentarius,
which Kepler's scholars first observed September 30,
O.S. 1604, with a light exceeding that of Jupiter, though the
night before it was not to be seen; and from that time it decreased by
little and little, and in 15 or 16 months entirely disappeared. Such a
new star appearing with an unusual splendor is said to have moved Hipparchus
to observe, and make a catalogue of, the fixed stars. As to those fixed
stars that appear and disappear by turns, and increase slowly and by
degrees, and scarcely ever exceed the stars of the third magnitude, they
seem to be of another kind, which revolve about their axes, and, having
a light and a dark side, shew those two different sides by turns. The
vapours which arise from the sun, the fixed stars, and the tails of the
comets, may meet at last with, and fall into, the atmospheres of the
planets by their gravity, and there be condensed and turned into water
and humid spirits; and from thence, by a slow heat, pass gradually into
the form of salts, and sulphurs, and tinctures, and mud, and clay, and
sand, and stones, and coral, and other terrestrial substances.
< Book 3.2
> Book 3.4
Table of Contents
Index