Section V.
Of the density and compression of fluids; and of hydrostatics.
The Definition of a Fluid.
A fluid is any body whose parts yield to any force impressed on it, by yielding, are easily moved among themselves.
Proposition xix. Theorem xiv
All the parts of a homogeneous and unmoved fluid included in any unmoved vessel, and compressed on every side (setting aside the consideration of condensation, gravity, and all centripetal forces), will be equally pressed on every side, and remain in their places without any motion arising from that pressure.
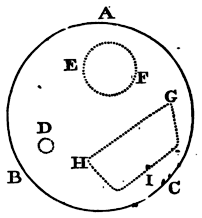
Case 1. Let a fluid be included in the spherical vessel ABC, arid uniformly compressed on every side: I say, that no part of it will be moved by that pressure. For if any part, as D, be moved, all such parts at the same distance from the centre on every side must necessarily be moved at the same time by a like motion; because the pressure of them all is similar and equal; and all other motion is excluded that does not arise from that pressure. But if these parts come all of them nearer to the centre, the fluid must be condensed towards the centre, contrary to the supposition. If they recede from it, the fluid must be condensed towards the circumference; which is also contrary to the supposition. Neither can they move in any one direction retaining their distance from the centre, because for the same reason, they may move in a contrary direction; but the same part cannot be moved contrary ways at the same time. Therefore no part of the fluid will be moved from its place. Q.E.D.
Case 2. I say now, that all the spherical parts of this fluid are equally pressed on every side. For let EF be a spherical part of the fluid; if this be not pressed equally on every side, augment the lesser pressure till it be pressed equally on every side; and its parts (by Case 1) will remain in their places. But before the increase of the pressure, they would remain in their places (by Case 1); and by the addition of a new pressure they will be moved, by the definition of a fluid, from those places. Now these two conclusions contradict each other. Therefore it was false to say that the sphere EF was not pressed equally on every side. Q.E.D.
Case 3. I say besides, that different spherical parts have equal pressures. For the contiguous spherical parts press each other mutually and equally in the point of contact (by Law III). But (by Case 2) they are pressed on every side with the same force. Therefore any two spherical parts not contiguous, since an intermediate spherical part can touch both, will be pressed with the same force. Q.E.D.
Case 4. I say now, that all the parts of the fluid are every where pressed equally. For any two parts may be touched by spherical parts in any points whatever; and there they will equally press those spherical parts (by Case 3), and are reciprocally equally pressed by them (by Law III). Q.E.D.
Case 5. Since, therefore, any part GHI of the fluid is inclosed by the rest of the fluid as in a vessel, and is equally pressed on every side; and also its parts equally press one another, and are at rest among themselves; it is manifest that all the parts of any fluid as GHI, which is pressed equally on every side, do press each other mutually and equally, and are at rest among themselves. Q.E.D.
Case 6. Therefore if that fluid be included in a vessel of a yielding substance, or that is not rigid, and be not equally pressed on every side, the same will give way to a stronger pressure, by the Definition of fluidity.
Case 7. And therefore, in an inflexible or rigid vessel, a fluid will not sustain a stronger pressure on one side than on the other, but will give way to it, and that in a moment of time; because the rigid side of the vessel does not follow the yielding liquor. But the fluid, by thus yielding, will press against the opposite side, and so the pressure will tend on every side to equality. And because the fluid, as soon as it endeavours to recede from the part that is most pressed, is withstood by the resistance of the vessel on the opposite side, the pressure will on every side be reduced to equality, in a moment of time, without any local motion: and from thence the parts of the fluid (by Case 5) will press each other mutually and equally, and be at rest among themselves. Q.E.D.
Cor. Whence neither will a motion of the parts of the fluid among themselves be changed by a pressure communicated to the external superficies, except so far as either the figure of the superficies may be somewhere altered, or that all the parts of the fluid, by pressing one another more in tensely or remissly, may slide with more or less difficulty among them selves.
Proposition xx. Theorem xv.
If all the parts of a spherical fluid, homogeneous at equal distances from the centre, lying on a spherical concentric bottom, gravitate towards the centre of the whole, the bottom will sustain the weight of a cylinder, whose base is equal to the superficies of the bottom, and whose altitude is the same with that of the incumbent fluid.
Let DHM be the superficies of the bottom, and AEI the upper
superficies of the fluid. Let the fluid be distinguished into
concentric orbs of equal thickness, by the innumerable spherical
superficies BFK, CGL: and
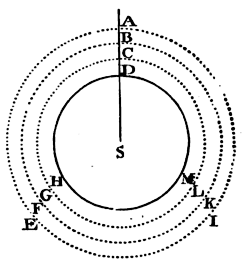 conceive the force of gravity to act only in the upper superficies of
every orb, and the actions to be equal on the equal parts of all the
superficies. Therefore the upper superficies AE is pressed by the
single force of its own gravity, by which all the parts of the upper
orb, and the second superficies BFK, will (by Prop. XIX), according to
its measure, be equally pressed. The second superficies BFK is pressed
likewise by the force of its own gravity, which, added to the former
force, makes the pressure double. The third superficies GGL is,
according to its measure, acted on by this pressure and the force of
its own gravity besides, which makes its pressure triple. And in like
manner the fourth superficies receives a quadruple pressure, the fifth
superficies a quintuple, and so on. Therefore the pressure acting on
every superficies is not as the solid quantity of the incumbent fluid,
but as the number of the orbs reaching to the upper surface of the
fluid; and is equal to the gravity of the lowest orb multiplied by the
number of orbs: that is, to the gravity of a solid whose ultimate
ratio to the cylinder above-mentioned (when the number of the orbs is
increased and their thickness diminished, ad infinitum, so
that the action of gravity from the lowest superficies to the
uppermost may become continued) is the ratio of equality. Therefore
the lowest superficies sustains the weight of the cylinder above
determined. Q.E.D. And by a like reasoning the
Proposition will be evident, where the gravity of the fluid decreases
in any assigned ratio of the distance from the centre, and also where
the fluid is more rare above and denser below. Q.E.D.
conceive the force of gravity to act only in the upper superficies of
every orb, and the actions to be equal on the equal parts of all the
superficies. Therefore the upper superficies AE is pressed by the
single force of its own gravity, by which all the parts of the upper
orb, and the second superficies BFK, will (by Prop. XIX), according to
its measure, be equally pressed. The second superficies BFK is pressed
likewise by the force of its own gravity, which, added to the former
force, makes the pressure double. The third superficies GGL is,
according to its measure, acted on by this pressure and the force of
its own gravity besides, which makes its pressure triple. And in like
manner the fourth superficies receives a quadruple pressure, the fifth
superficies a quintuple, and so on. Therefore the pressure acting on
every superficies is not as the solid quantity of the incumbent fluid,
but as the number of the orbs reaching to the upper surface of the
fluid; and is equal to the gravity of the lowest orb multiplied by the
number of orbs: that is, to the gravity of a solid whose ultimate
ratio to the cylinder above-mentioned (when the number of the orbs is
increased and their thickness diminished, ad infinitum, so
that the action of gravity from the lowest superficies to the
uppermost may become continued) is the ratio of equality. Therefore
the lowest superficies sustains the weight of the cylinder above
determined. Q.E.D. And by a like reasoning the
Proposition will be evident, where the gravity of the fluid decreases
in any assigned ratio of the distance from the centre, and also where
the fluid is more rare above and denser below. Q.E.D.
Cor. 1. Therefore the bottom is not pressed by the whole weight of the incumbent fluid, but only sustains that part of it which is described in the Proposition; the rest of the weight being sustained archwise by the spherical figure of the fluid.
Cor. 2. The quantity of the pressure is the same always at equal distances from the centre, whether the superficies pressed be parallel to the horizon, or perpendicular, or oblique; or whether the fluid, continued upwards from the compressed superficies, rises perpendicularly in a rectilinear direction, or creeps obliquely through crooked cavities and canals, whether those passages be regular or irregular, wide or narrow. That the pressure is not altered by any of these circumstances, may be collected by applying the demonstration of this Theorem to the several cases of fluids.
Cor. 3. From the same demonstration it may also be collected (by Prop. XIX), that the parts of a heavy fluid acquire no motion among themselves by the pressure of the incumbent weight, except that motion which arises from condensation.
Cor. 4. And therefore if another body of the same specific gravity, incapable of condensation, be immersed in this fluid, it will acquire no motion by the pressure of the incumbent weight: it will neither descend nor ascend, nor change its figure. If it be spherical, it will remain so, notwithstanding the pressure; if it be square, it will remain square; and that, whether it be soft or fluid; whether it swims freely in the fluid, or lies at the bottom. For any internal part of a fluid is in the same state with the submersed body; and the case of all submersed bodies that have the same magnitude, figure, and specific gravity, is alike. If a submersed body, retaining its weight, should dissolve and put on the form of a fluid, this body, if before it would have ascended, descended, or from any pressure assume a new figure, would now likewise ascend, descend, or put on a new figure; and that, because its gravity and the other causes of its motion remain. But (by Case 5, Prop. XIX) it would now be at rest, and retain its figure. Therefore also in the former case.
Cor. 5. Therefore a body that is specifically heavier than a fluid contiguous to it will sink; and that which is specifically lighter will ascend, and attain so much motion and change of figure as that excess or defect of gravity is able to produce. For that excess or defect is the same thing as an impulse, by which a body, otherwise in equilibrio with the parts of the fluid, is acted on; and may be compared with the excess or defect of a weight in one of the scales of a balance.
Cor. 6. Therefore bodies placed in fluids have a twofold gravity the one true and absolute, the other apparent, vulgar, and comparative. Absolute gravity is the whole force with which the body tends downwards; relative and vulgar gravity is the excess of gravity with which the body tends downwards more than the ambient fluid. By the first kind of gravity the parts of all fluids and bodies gravitate in their proper places; and therefore their weights taken together compose the weight of the whole. For the whole taken together is heavy, as may be experienced in vessels full of liquor; and the weight of the whole is equal to the weights of all the parts, and is therefore composed of them. By the other kind of gravity bodies do not gravitate in their places; that is, compared with one another, they do not preponderate, but, hindering one another's endeavours to descend, remain in their proper places, as if they were not heavy. Those things which are in the air, and do not preponderate, are commonly looked on as not heavy. Those which do preponderate are commonly reckoned heavy, in as much as they are not sustained by the weight of the air. The common weights are nothing else but the excess of the true weights above the weight of the air. Hence also, vulgarly, those things are called light which are less heavy, and, by yielding to the preponderating air, mount upwards. But these are only comparatively light, and not truly so, because they descend in vacuo. Thus, in water, bodies which, by their greater or less gravity, descend or ascend, are comparatively and apparently heavy or light; and their comparative and apparent gravity or levity is the excess or defect by which their true gravity either exceeds the gravity of the water or is exceeded by it. But those things which neither by preponderating descend, nor, by yielding to the preponderating fluid, ascend, although by their true weight they do increase the weight of the whole, yet comparatively, and in the sense of the vulgar, they do not gravitate in the water. For these cases are alike demonstrated.
Cor. 7. These things which have been demonstrated concerning gravity take place in any other centripetal forces.
Cor. 8. Therefore if the medium in which any body moves be acted on either by its own gravity, or by any other centripetal force, and the body be urged more powerfully by the same force; the difference of the forces is that very motive force, which, in the foregoing Propositions, I have considered as a centripetal force. But if the body be more lightly urged by that force, the difference of the forces becomes a centrifugal force, and is to be considered as such.
Cor. 9. But since fluids by pressing the included bodies do not change their external figures, it appears also (by Cor. Prop. XIX) that they will not change the situation of their internal parts in relation to one another; and therefore if animals were immersed therein, and that all sensation did arise from the motion of their parts, the fluid will neither hurt the immersed bodies, nor excite any sensation, unless so far as those bodies may be condensed by the compression. And the case is the same of any system of bodies encompassed with a compressing fluid. All the parts of the system will be agitated with the same motions as if they were placed in a vacuum, and would only retain their comparative gravity; unless so far as the fluid may somewhat resist their motions, or be requisite to conglutinate them by compression.
Proposition xxi. Theorem xvi.
Let the density of any fluid be proportional to the compression, and its parts be attracted downwards by a centripetal force reciprocally proportional to the distances from the centre: I say, that, if those distances be taken continually proportional, the densities of the fluid at the same distances will be also continually proportional.
Let ATV denote the spherical bottom of the fluid, S the centre, SA,
SB, SC, SD, SE, SF, &c., distances continually proportional. Erect
the perpendiculars AH, BI, CK, DL, EM, FN, &c., which shall be as
the densities of the medium in the places A, B, C, D, E, F; and the
specific gravities in those places will be AH
AS, BI
BS, CK
CS, &c., or, which is all one, as
AH
AB, BI
BC, CK
CD, &c. Suppose, first, these
gravities to be uniformly continued from A to B, from B to C, from C
to D, &c., the decrements in the points
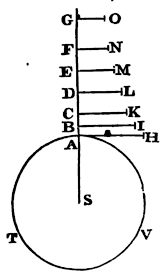 B, C, D, &c., being taken by steps. And these gravities drawn into
the altitudes AB, BC, CD, &c., will give the pressures AH, BI, CK,
&c., by which the bottom ATV is acted on (by Theor. XV). Therefore
the particle A sustains all the pressures AH, BI, CK, DL, &c.,
proceeding in infinitum; and the particle B sustains the
pressures of all but the first AH; and the particle C all but the two
first AH, BI; and so on: and therefore the density AH of the first
particle A is to the density BI of the second particle B as the sum of
all AH + BI + CK + DL, in infinitum, to the sum of all BI +
CK + DL, &c. And BI the density of the second particle B is to CK
the density of the third C, as the sum of all BI + CK + DL, &c.,
to the sum of all CK + DL, &c. Therefore these sums are
proportional to their differences AH, BI, CK, &c., and therefore
continually proportional (by Lem. 1 of this Book); and therefore the
differences AH, BI, CK, &c., proportional to the sums, are also
continually proportional. Wherefore since the densities in the places
A, B, C, &c., are as AH, BI, CK, &c., they will also be
continually proportional. Proceed intermissively, and, ex aequo,
at the distances SA, SC, SE, continually proportional, the densities
AH, CK, EM will be continually proportional. And by the same
reasoning, at any distances SA, SD, SG, continually proportional, the
densities AH, DL, GO, will be continually proportional. Let now the
points A, B, C, D, E, &c., coincide, so that the progression of
the specific gravities from the bottom A to the top of the fluid may
be made continual; and at any distances SA, SD, SG, continually
proportional, the densities AH, DL, GO, being all along continually
proportional, will still remain continually proportional.
Q.E.D.
B, C, D, &c., being taken by steps. And these gravities drawn into
the altitudes AB, BC, CD, &c., will give the pressures AH, BI, CK,
&c., by which the bottom ATV is acted on (by Theor. XV). Therefore
the particle A sustains all the pressures AH, BI, CK, DL, &c.,
proceeding in infinitum; and the particle B sustains the
pressures of all but the first AH; and the particle C all but the two
first AH, BI; and so on: and therefore the density AH of the first
particle A is to the density BI of the second particle B as the sum of
all AH + BI + CK + DL, in infinitum, to the sum of all BI +
CK + DL, &c. And BI the density of the second particle B is to CK
the density of the third C, as the sum of all BI + CK + DL, &c.,
to the sum of all CK + DL, &c. Therefore these sums are
proportional to their differences AH, BI, CK, &c., and therefore
continually proportional (by Lem. 1 of this Book); and therefore the
differences AH, BI, CK, &c., proportional to the sums, are also
continually proportional. Wherefore since the densities in the places
A, B, C, &c., are as AH, BI, CK, &c., they will also be
continually proportional. Proceed intermissively, and, ex aequo,
at the distances SA, SC, SE, continually proportional, the densities
AH, CK, EM will be continually proportional. And by the same
reasoning, at any distances SA, SD, SG, continually proportional, the
densities AH, DL, GO, will be continually proportional. Let now the
points A, B, C, D, E, &c., coincide, so that the progression of
the specific gravities from the bottom A to the top of the fluid may
be made continual; and at any distances SA, SD, SG, continually
proportional, the densities AH, DL, GO, being all along continually
proportional, will still remain continually proportional.
Q.E.D.
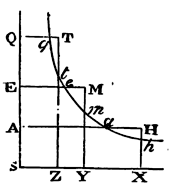
Cor. Hence if the density of the fluid in two places, as A and E, be given, its density in any other place Q may be collected. With the centre S, and the rectangular asymptotes SQ, SX, describe an hyperbola cutting the perpendiculars AH, EM, QT in a, e, and q, as also the perpendiculars HX, MY, TZ, let fall upon the asymptote SX, in h, m, and t. Make the area YmtZ to the given area YmhX as the given area EeqQ to the given area EeaA; and the line Zt produced will cut off the line QT proportional to the density. For if the lines SA, SE, SQ are continually proportional, the areas EeqQ, EeaA will be equal, and thence the areas YmtZ, XhmY, proportional to them, will be also equal; and the lines SX, SY, SZ, that is, AH, EM, QT continually proportional, as they ought to be. And if the lines SA, SE, SQ, obtain any other order in the series of continued proportionals, the lines AH, EM, QT, because of the proportional hyperbolic areas, will obtain the same order in another series of quantities continually proportional.
Proposition xxii. Theorem xvii.
Let the density of any fluid be proportional to the compression, and its parts be attracted downwards by a gravitation reciprocally proportional to the squares of the distances from the centre: I say, that if the distances be taken in harmonic progression, the densities of the fluid at those distances will be in a geometrical progression.
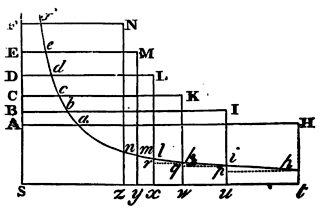
Let S denote the centre, and SA, SB, SC, SD, SE, the distances in
geometrical progression. Erect the perpendiculars AH, BI, CK, &c.,
which shall be as the densities of the fluid in the places A, B, C, D,
E, &c., and the specific gravities thereof in those places will be
as AH
SA2,
BI
SB2,
CK
SC2, &c. Suppose these
gravities to be uniformly continued, the first from A to B, the second
from B to C, the third from C to D, &c. And these drawn into the
altitudes AB, BC, CD, DE, &c., or, which is the same thing, into
the distances SA, SB, SC, &c., proportional to those altitudes,
will give AH
SA, BI
SB, CK
SC, &c., the exponents of the
pressures. Therefore since the densities are as the sums of those
pressures, the differences AH − BI, BI − CK, &c., of the densities
will be as the differences of those sums AH
SA, BI
SB, CK
SC, &c. With the centre S, and the
asymptotes SA, Sx, describe any hyperbola, cutting the
perpendiculars AH, BI, CK, &c., in a, b, c, &c., and
the perpendiculars Ht, In, Kw, let fall
upon the asymptote Sx, in h, i, k; and the
differences of the densities tu, uw, &c., will be as
AH
SA, BI
SB, &c. And the rectangles tu
x th, uw x ui, &c., or tp, uq, &c., as
AH x th
SA, BI
x ui
SB, &c., that is, as Aa, Bb,
&c. For, by the nature of the hyperbola, SA is to AH or St
as th to Ac, and therefore
AH x th
SA is equal to Aa. And, by a
like reasoning, BI
x ui
SB is equal to Bb, &c. But
Aa, Bb, Cc, &c., are continually
proportional, and therefore proportional to their differences Aa
− Bb, Bb − Cc, &c., therefore the
rectangles tp, uq, &c., are proportional to those
differences; as also the sums of the rectangles tp + uq, or
tp + uq + wr to the sums of the differences Aa − Cc
or Aa − Dd. Suppose several of these terms, and the
sum of all the differences, as Aa − Ff, will be
proportional to the sum of all the rectangles, as zthn.
Increase the number of terms, and diminish the distances of the points
A, B, C, &c., in infinitum, and those rectangles will
become equal to the hyperbolic area zthn, and therefore the
difference Aa − Ff is proportional to this area.
Take now any distances, as SA, SD, SF, in harmonic progression, and
the differences Aa − Dd, Dd − Ff
will be equal; and therefore the areas thlx, xluz,
proportional to those differences will be equal among themselves, and
the densities St, Sx, Sz, that is, AH, DL,
FN, continually proportional. Q.E.D.
Cor. Hence if any two densities of the fluid, as AH and BI, be given, the area thiu, answering to their difference tu, will be given; and thence the density FN will be found at any height SF, by taking the area thnz to that given area thiu as the difference Aa − Ff to the difference Aa − Bb.
Scholium.
By a like reasoning it may be proved, that if the gravity of the
particles of a fluid be diminished in a triplicate ratio of the
distances from the centre; and the reciprocals of the squares of the
distances SA, SB, SC, &c., (namely, SA3
SA2,
SA3
SB2,
SA3
SC2 ) be taken in an
arithmetical progression, the densities AH, BI, CK, &c., will be
in a geometrical progression. And if the gravity be diminished in a
quadruplicate ratio of the distances, and the reciprocals of the cubes
of the distances (as SA4
SA3,
SA4
SB3,
SA4
SC3, &c.,) be taken in
arithmetical progression, the densities AH, BI, CK, &c., will be
in geometrical progression. And so in infinitum. Again; if
the gravity of the particles of the fluid be the same at all
distances, and the distances be in arithmetical progression, the
densities will be in a geometrical progression as Dr. Halley
has found. If the gravity be as the distance, and the squares of the
distances be in arithmetical progression, the densities will be in
geometrical progression. And so in infinitum. These things
will be so, when the density of the fluid condensed by compression is
as the force of compression; or, which is the same thing, when the
space possessed by the fluid is reciprocally as this force. Other laws
of condensation may be supposed, as that the cube of the compressing
force may be as the biquadrate of the density;
or the triplicate ratio of the force the same with the quadruplicate
ratio of the density: in which case, if the gravity he reciprocally as
the square of the distance from the centre; the density will be
reciprocally as the cube of the distance. Suppose that the cube of the
compressing force be as the quadrato-cube of the density; and if the
gravity be reciprocally as the square of the distance, the density
will be reciprocally in a sesquiplicate ratio of the distance. Suppose
the compressing force to be in a duplicate ratio of the density, and
the gravity reciprocally in a duplicate ratio of the distance, and the
density will be reciprocally as the distance. To run over all the
cases that might be offered would be tedious. But as to our own air,
this is certain from experiment, that its density is either
accurately, or very nearly at least, as the compressing force; and
therefore the density of the air in the atmosphere of the earth is as
the weight of the whole incumbent air, that is, as the height of the
mercury in the barometer.
Proposition xxiii. Theorem xviii.
If a fluid be composed of particles mutually flying each other, and the density be as the compression, the centrifugal forces of the particles will be reciprocally proportional to the distances of their centres. And, vice versa, particles flying each other, with forces that are reciprocally proportional to the distances of their centres, compose an elastic fluid, whose density is as the compression.
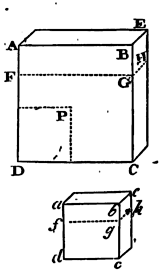
Let the fluid be supposed to be included in a cubic space ACE, and then to be reduced by compression into a lesser cubic space ace; and the distances of the particles retaining a like situation with respect to each other in both the spaces, will be as the sides AB, ab of the cubes; and the densities of the mediums will be reciprocally as the containing spaces AB³, ab³. In the plane side of the greater cube ABCD take the square DP equal to the plane side db of the lesser cube: and, by the supposition, the pressure with which the square DP urges the inclosed fluid will be to the pressure with which that square db urges the inclosed fluid as the densities of the mediums are to each other, that is, as ab³ to AB³. But the pressure with which the square DB urges the included fluid is to the pressure with which the square DP urges the same fluid as the square DB to the square DP, that is, as AB² to ab². Therefore, ex aequo, the pressure with which the square DB urges the fluid is to the pressure with which the square db urges the fluid as ab to AB. Let the planes FGH, fgh, be drawn through the middles of the two cubes, and divide the fluid into two parts. These parts will press each other mutually with the same forces with which they are themselves pressed by the planes AC, ac, that is, in the proportion of ab to AB: and therefore the centrifugal forces by which these pressures are sustained are in the same ratio. The number of the particles being equal, and the situation alike, in both cubes, the forces which all the particles exert, according to the planes FGH, fgh, upon all, are as the forces which each exerts on each. Therefore the forces which each exerts on each, according to the plane FGH in the greater cube, are to the forces which each exerts on each, according to the plane fgh in the lesser cube, as ab to AB, that is, reciprocally as the distances of the particles from each other. Q.E.D.
And, vice versa, if the forces of the single particles are reciprocally as the distances, that is, reciprocally as the sides of the cubes AB, ab; the sums of the forces will be in the same ratio, and the pressures of the sides DB, db as the sums of the forces; and the pressure of the square DP to the pressure of the side DB as ab² to AB² . And, ex aequo, the pressure of the square DP to the pressure of the side db as ab³ to AB³; that is, the force of compression in the one to the force of compression in the other as the density in the former to the density in the latter. Q.E.D.
Scholium.
By a like reasoning, if the centrifugal forces of the particles are reciprocally in the duplicate ratio of the distances between the centres, the cubes of the compressing forces will be as the biquadrates of the densities. If the centrifugal forces be reciprocally in the triplicate or quadruplicate ratio of the distances, the cubes of the compressing forces will be as the quadratocubes, or cubo-cubes of the densities. And universally, if D be put for the distance, and E for the density of the compressed fluid, and the centrifugal forces be reciprocally as any power Dn of the distance, whose index is the number n, the compressing forces will be as the cube roots of the power En+2, whose index is the number n + 2; and the contrary. All these things are to be understood of particles whose centrifugal forces terminate in those particles that are next them, or are diffused not much further. We have an example of this in magnetical bodies. Their attractive virtue is terminated nearly in bodies of their own kind that are next them. The virtue of the magnet is contracted by the interposition of an iron plate, and is almost terminated at it: for bodies further off are not attracted by the magnet so much as by the iron plate. If in this manner particles repel others of their own kind that lie next them, but do not exert their virtue on the more remote, particles of this kind will compose such fluids as are treated of in this Proposition. If the virtue of any particle diffuse itself every way in infinitum, there will be required a greater force to produce an equal condensation of a greater quantity of the fluid. But whether elastic fluids do really consist of particles so repelling each other, is a physical question. We have here demonstrated mathematically the property of fluids consisting of particles of this kind, that hence philosophers may take occasion to discuss that question.