Section ii.
Of the motion of bodies that are resisted in the duplicate ratio of their velocities.
Proposition v. Theorem iii.
If a body is resisted in the duplicate ratio of its velocity, and moves by its innate force only through a similar medium; and the times be taken in a geometrical progression, proceeding from less to greater terms: I say, that the velocities at the beginning of each of the times are in the same geometrical progression inversely; and that the spaces are equal, which are described in each of the times.
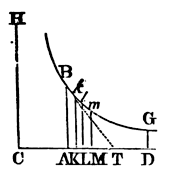
For since the resistance of the medium is proportional to the square of the velocity, and the decrement of the velocity is proportional to the resistance: if the time be divided into innumerable equal particles, the squares of the velocities at the beginning of each of the times will be proportional to the differences of the same velocities. Let those particles of time be AK, KL, LM, &c., taken in the right line CD; and erect the perpendiculars AB, Kk, Ll, Mm, &c., meeting the hyperbola BklmG, described with the centre C, and the rectangular asymptotes CD, CH, in B, k, l, m, &c.; then AB will be to Kk as CK to CA, and, by division, AB − Kk to Kk as AK to CA, and alternately, AB − Kk to AK as Kk to CA; and therefore as AB x Kk to AB x CA. Therefore since AK and AB x CA are given, AB − Kk will be as AB x KA; and, lastly, when AB and Kk coincide, as AB². And, by the like reasoning, Kk − Ll, Ll − Mm, &c., will be as Kk², Ll², &c. Therefore the squares of the lines AB, Kk, Ll, Mm, &c., are as their differences; and, therefore, since the squares of the velocities were shewn above to be as their differences, the progression of both will be alike. This being demonstrated it follows also that the areas described by these lines are in a like progression with the spaces described by these velocities. Therefore if the velocity at the beginning of the first time AK be expounded by the line AB, and the velocity at the beginning of the second time KL by the line Kk and the length described in the first time by the area AKkB, all the following velocities will be expounded by the following lines Ll, Mm, &c. and the lengths described, by the areas Kl, Lm. &c. And, by composition, if the whole time be expounded by AM, the sum of its parts, the whole length described will be expounded by AMmB the sum of its parts. Now conceive the time AM to be divided into the parts AK, KL, LM, &c. so that CA, CK, CL, CM, &c. may be in a geometrical progression; and those parts will be in the same progression, and the velocities AB, Kk, Ll, Mm, &c., will be in the same progression inversely, and the spaces described Ak, Kl, Lm, &c., will be equal. Q.E.D.
Cor. 1. Hence it appears, that if the time be expounded by any part AD of the asymptote, and the velocity in the beginning of the time by the ordinate AB, the velocity at the end of the time will be expounded by the ordinate DG; and the whole space described by the adjacent hyperbolic area ABGD; and the space which any body can describe in the same time AD, with the first velocity AB, in a non-resisting medium, by the rectangle AB x AD.
Cor 2. Hence the space described in a resisting medium is given, by taking it to the space described with the uniform velocity AB in a nonresisting medium, as the hyperbolic area ABGD to the rectangle AB x AD.
Cor. 3. The resistance of the medium is also given, by making it equal, in the very beginning of the motion, to an uniform centripetal force, which could generate, in a body falling through a non-resisting medium, the velocity AB in the time AC. For if BT be drawn touching the hyperbola in B, and meeting the asymptote in T, the right line AT will be equal to AC, and will express the time in which the first resistance, uniformly continued, may take away the whole velocity AB
Cor. 4. And thence is also given the proportion of this resistance to the force of gravity, or any other given centripetal force.
Cor. 5. And, vice versa, if there is given the proportion of the resistance to any given centripetal force, the time AC is also given, in which a centripetal force equal to the resistance may generate any velocity as AB; and thence is given the point B, through which the hyperbola, having CH, CD for its asymptotes, is to be described; as also the space ABGD, which a body, by beginning its motion with that velocity AB, can describe in any time AD, in a similar resisting medium.
Proposition vi. Theorem iv.
Homogeneous and equal spherical bodies, opposed by resistances that are in the duplicate ratio of the velocities, and moving on by their innate force only, will, in times which are reciprocally as the velocities at the beginning, describe equal spaces, and lose parts of their velocities proportional to the wholes.
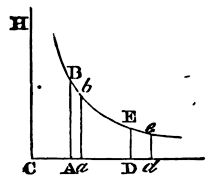
To the rectangular asymptotes CD, CH describe any hyperbola BbEe, cutting the perpendiculars AB, ab, DE, de in B, b, E, e; let the initial velocities be expounded by the perpendiculars AB, DE, and the times by the lines Aa, Dd. Therefore as Aa is to Dd, so (by the hypothesis) is DE to AB, and so (from the nature of the hyperbola) is CA to CD; and, by composition, so is Ca to Cd. Therefore the areas ABba, DEed, that is, the spaces described, are equal among themselves, and the first velocities AB, DE are proportional to the last ab, de; and therefore, by division, proportional to the parts of the velocities lost, AB − ab, DE − de. Q.E.D.
Proposition vii. Theorem V.
If spherical bodies are resisted in the duplicate ratio of their velocities, in times which are as the first motions directly, and the first resistances inversely, they will lose parts of their motions proportional to the wholes, and will describe spaces proportional to those times and the first velocities conjunctly.
For the parts of the motions lost are as the resistances and times conjunctly. Therefore, that those parts may be proportional to the wholes, the resistance and time conjunctly ought to be as the motion. Therefore the time will be as the motion directly and the resistance inversely. Wherefore the particles of the times being taken in that ratio, the bodies will always lose parts of their motions proportional to the wholes, and therefore will retain velocities always proportional to their first velocities. And because of the given ratio of the velocities, they will always describe spaces which are as the first velocities and the times conjunctly. Q.E.D.
Cor. 1. Therefore if bodies equally swift are resisted in a duplicate ratio of their diameters, homogeneous globes moving with any velocities whatsoever, by describing spaces proportional to their diameters, will lose parts of their motions proportional to the wholes. For the motion of each globe will be as its velocity and mass conjunctly, that is, as the velocity and the cube of its diameter; the resistance (by supposition) will be as the square of the diameter and the square of the velocity conjunctly; and the time (by this proposition) is in the former ratio directly, and in the latter inversely, that is, as the diameter directly and the velocity inversely; and therefore the space, which is proportional to the time and velocity is as the diameter.
Cor. 2. If bodies equally swift are resisted in a sesquiplicate ratio of their diameters, homogeneous globes, moving with any velocities whatsoever, by describing spaces that are in a sesquiplicate ratio of the diameters, will lose parts of their motions proportional to the wholes.
Cor. 3. And universally; if equally swift bodies are resisted in the ratio of any power of the diameters, the spaces, in which homogeneous globes, moving with any velocity whatsoever, will lose parts of their motions proportional to the wholes, will be as the cubes of the diameters applied to that power. Let those diameters be D and E; and if the resistances, where the velocities are supposed equal, are as Dn and En; the spaces in which the globes, moving with any velocities whatsoever, will lose parts of their motions proportional to the wholes, will be as D3−n and E3−n. And therefore homogeneous globes, in describing spaces proportional to D3−n and E3−n, will retain their velocities in the same ratio to one another as at the beginning.
Cor. 4. Now if the globes are not homogeneous, the space described by the denser globe must be augmented in the ratio of the density. For the motion, with an equal velocity, is greater in the ratio of the density, and the time (by this Prop.) is augmented in the ratio of motion directly, and the space described in the ratio of the time.
Cor. 5. And if the globes move in different mediums, the space, in a medium which, caeteris paribus, resists the most, must be diminished in the ratio of the greater resistance. For the time (by this Prop.) will be diminished in the ratio of the augmented resistance, and the space in the ratio of the time.
Lemma ii.
The moment of any genitum is equal to the moments of each of the generating sides drawn into the indices of the powers of those sides, and into their co-efficients continually.
I call any quantity a genitum which is not made by addition or subduction of divers parts, but is generated or produced in arithmetic by the multiplication, division, or extraction of the root of any terms whatsoever; in geometry by the invention of contents and sides, or of the extremes and means of proportionals. Quantities of this kind are products, quotients, roots, rectangles, squares, cubes, square and cubic sides, and the like. These quantities I here consider as variable and indetermined, and increasing or decreasing, as it were, by a perpetual motion or flux; and I understand their momentaneous increments or decrements by the name of moments; so that the increments may be esteemed as added or affirmative moments; and the decrements as subducted or negative ones. But take care not to look upon finite particles as such. Finite particles are not moments, but the very quantities generated by the moments. We are to conceive them as the just nascent principles of finite magnitudes. Nor do we in this Lemma regard the magnitude of the moments, but their first proportion, as nascent. It will be the same thing, if, instead of moments, we use either the velocities of the increments and decrements (which may also be called the motions, mutations, and fluxions of quantities), or any finite quantities proportional to those velocities. The co-efficient of any generating side is the quantity which arises by applying the genitum to that side.
Wherefore the sense of the Lemma is, that if the moments of any
quantities A, B, C, &c., increasing or decreasing by a perpetual
flux, or the velocities of the mutations which are proportional to
them, be called a, b, c, &c., the moment or mutation of
the generated rectangle AB will be aB + bA; the
moment of the generated content ABC will be aBC + bAC
+ cAB; and the moments of the generated powers A², A³, A4,
A½, A3/2, A⅓, A⅔,
A−1, A−2, A−½ will be 2aA, 3aA²,
4aA³, ½aA−½, 3/2aA½,
⅓aA−⅔, ⅔aA−⅓, −aA−2,
−2aA−3, −½aA−3/2
respectively; and in general, that the moment of any power A
n
m, will be n
m aA
n−m
m. Also, that the moment of the
generated quantity A²B bill be 2aAB + bA²; the moment of the
generated quantity A³ B4 C² will be 3aA² B4
C² + 4bA³B³C² + 2cA³B4C; and the moment
of the generated quantity A3
B2 or A³B−2 will
be 3aA²B−2−2bA³B−3; and so on.
The Lemma is thus demonstrated.
Case 1. Any rectangle, as AB, augmented by a perpetual flux, when, as yet, there wanted of the sides A and B half their moments ½a and ½b, was A−½a into B−½b, or AB − ½a B − ½b A + ¼ab; but as soon as the sides A and B are augmented by the other half moments, the rectangle becomes A + ½a into B + ½b, or AB + ½a B + ½b A + ¼ab. From this rectangle subduct the former rectangle, and there will remain the excess aB + bA. Therefore with the whole increments a and b of the sides, the increment aB + bA of the rectangle is generated. Q.E.D.
Case 2. Suppose AB always equal to G, and then the moment of the content ABC or GC (by Case 1) will be gC + cG, that is (putting AB and aB + bA for G and g), aBC + bAC + cAB. And the reasoning is the same for contents under ever so many sides. Q.E.D.
Case 3. Suppose the sides A, B, and C, to be always equal among themselves; and the moment aB + bA, of A², that is, of the rectangle AB, will be 2aA; and the moment aBC + bAC + cAB of A³, that is, of the content ABC, will be 3aA². And by the same reasoning the moment of any power An is naAn−1. Q.E.D
Case 4. Therefore since
1
A into A is 1, the moment of
1
A drawn into A,
together with 1
A drawn into a, will be the
moment of 1, that is, nothing. Therefore the moment of
1
A, or of A−1, is
−a
A2. And generally since
1
An into An is
1, the moment of 1
An drawn into An
together with 1
An into naAn−1
will be nothing. And, therefore, the moment of
1
An or A−n will
be −na
An+1. Q.E.D.
Case 5. And since A½ into A½
is A, the moment of A½ drawn into 2A½ will be a
(by Case 3); and, therefore, the moment of A½ will be
a
2A1/2 or ½aA−½.
And, generally, putting A
m
n equal to B, then Am
will be equal to Bn, and therefore maAm−1
equal to nbBn−1, and maA−1
equal to nbB−1, or nbA−
m
n; and therefore
m
naAm−n
n is equal to b,
that is, equal to the moment of A
m
n. Q.E.D.
Case 6. Therefore the moment of any generated quantity AmBn is the moment of Am drawn into Bn, together with the moment of Bn drawn into Am, that is, maAm−1 Bn + nbBn−1 Am; and that whether the indices m and n of the powers be whole numbers or fractions, affirmative or negative. And the reasoning is the same for contents under more powers. Q.E.D.
Cor. 1. Hence in quantities continually proportional, if one term is given, the moments of the rest of the terms will be as the same terms multiplied by the number of intervals between them nd the given term. Let A, B, C, D, E, F, be continually proportional; then if the term C is given, the moments of the rest of the terms will be among themselves as −2A, −B, D, 2E, 3F.
Cor. 2. And if in four proportionals the two means are given, the moments of the extremes will be as those extremes. The same is to be understood of the sides of any given rectangle.
Cor. 3. And if the sum or difference of two squares is given, the moments of the sides will be reciprocally as the sides.
Scholium.
In a letter of mine to Mr. J. Collins, dated December 10, 1672, having described a method of tangents, which I suspected to be the same with Slusius's method, which at that time was not made public, I subjoined these words: This is one particular, or rather a Corollary, of a general method, which extends itself, without any troublesome calculation, not only to the drawing of tangents to any curve lines, whether geometrical or mechanical, or any how respecting right lines or other curves, but also to the resolving other abstruser kinds of problems about the crookedness, areas, lengths, centres of gravity of curves, &c.; nor is it (as Hudden's method de Maximis & Minimis) limited to equations which are free from surd quantities. This method I have interwoven with that other of working in equations, by reducing them to infinite series. So far that letter. And these last words relate to a treatise I composed on that subject in the year 1671. The foundation of that general method is contained in the preceding Lemma.
Proposition viii. Theorem vi.
If a body in an uniform medium, being uniformly acted upon by the force of gravity, ascends or descends in a right line; and the whole space described be distinguished into equal parts, and in the beginning of each of the parts (by adding or subducting the resisting force of the medium to or from the force of gravity, when the body ascends or descends] you collect the absolute forces; I say, that those absolute forces are in a geometrical progression.
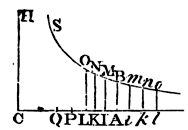
For let the force of gravity be expounded by the given line AC; the force of resistance by the indefinite line AK; the absolute force in the descent of the body by the difference KC: the velocity of the body by a line AP, which shall be a mean proportional between AK and AC, and therefore in a subduplicate ratio of the resistance; the increment of the resistance made in a given particle of time by the lineola KL, and the contemporaneous increment of the velocity by the lineola PQ; and with the centre C, and rectangular asymptotes CA, CH, describe any hyperbola BNS meeting the erected perpendiculars AB, KN, LO in B, N and O. Because AK is as AP², the moment KL of the one will be as the moment 2APQ of the other, that is, as AP x KC; for the increment PQ of the velocity is (by Law II) proportional to the generating force KC. Let the ratio of KL be compounded with the ratio KN, and the rectangle KL x KN will become as AP x KC x KN; that is (because the rectangle KC x KN is given), as AP. But the ultimate ratio of the hyperbolic area KNOL to the rectangle KL x KN becomes, when the points K and L coincide, the ratio of equality. Therefore that hyperbolic evanescent area is as AP. Therefore the whole hyperbolic area ABOL is composed of particles KNOL which are always proportional to the velocity AP; and therefore is itself proportional to the space described with that velocity. Let that area be now divided into equal parts as ABMI, IMNK, KNOL, &c., and the absolute forces AC, IC, KC, LC, &c., will be in a geometrical progression. Q.E.D. And by a like reasoning, in the ascent of the body, taking, on the contrary side of the point A, the equal areas ABmi, imnk, knol, &c., it will appear that the absolute forces AC, iC, kC, lC, &c., are continually proportional. Therefore if all the spaces in the ascent and descent are taken equal, all the absolute forces lC, kC, iC, AC, IC, KC, LC, &c., will be continually proportional. Q.E.D.
Cor. 1. Hence if the space described be expounded by the hyperbolic area ABNK, the force of gravity, the velocity of the body, and the resistance of the medium, may be expounded by the lines AC, AP, and AK respectively; and vice versa.
Cor. 2. And the greatest velocity which the body can ever acquire in an infinite descent will be expounded by the line AC.
Cor. 3. Therefore if the resistance of the medium answering to any given velocity be known, the greatest velocity will be found, by taking it to that given velocity in a ratio subduplicate of the ratio which the force of gravity bears to that known resistance of the medium.
Proposition ix. Theorem vii.
Supposing what is above demonstrated, I say, that if the tangents of the angles of the sector of a circle, and of an hyperbola, be taken proportional to the velocities, the radius being of a fit magnitude, all the time of the ascent to the highest place will be as the sector of the circle, and all the time of descending from the highest place as the sector of the hyperbola.
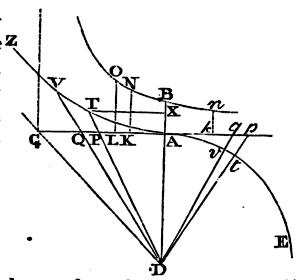
To the right line AC, which expresses the force of gravity, let AD be drawn perpendicular and equal. From the centre D with the semi-diameter AD describe as well the quadrant AtE of a circle, as the rectangular hyperbola AVZ, whose axis is AK, principal vertex A, and asymptote DC. Let Dp, DP be drawn; and the circular sector AtD will be as all the time of the ascent to the highest place; and the hyperbolic sector ATD as all the time of descent from the highest place; if so be that the tangents Ap, AP of those sectors be as the velocities.
Case 1. Draw Dvq cutting off the
moments or least particles tDv and qDp,
described in the same time, of the sector ADt and of the
triangle ADp. Since those particles (because of the common
angle D) are in a duplicate ratio of the sides, the particle tDv
will be as qDp x tD2
pD2, that is (because
tD is given), as qDp
pD2. But pD² is
AD² + Ap², that is, AD² + AD x Ak, or AD x Ck;
and qDp is ½AD x pq. Therefore tDv,
the particle of the sector, is as pq
Ck; that is, as the least decrement pq
of the velocity directly, and the force Ck which diminishes
the velocity, inversely; and therefore as the particle of time
answering to the decrement of the velocity. And, by composition, the
sum of all the particles tDv in the sector ADt
will be as the sum of the particles of time answering to each of the
lost particles pq of the decreasing velocity Ap,
till that velocity, being diminished into nothing, vanishes; that is,
the whole sector ADt is as the whole time of ascent to the
highest place. Q.E.D.
Case 2. Draw DQV cutting off the least
particles TDV and PDQ of the sector DAV, and of the triangle DAQ; and
these particles will be to each other as DT² to DP², that is (if TX
and AP are parallel), as DX² to DA² or TX² to AP²; and, by division,
as DX² − TX² to DA² − AP² . But, from the nature of the hyperbola, DX²
− TX² is AD²; and, by the supposition, AP² is AD x AK. Therefore the
particles are to each other as AD² to AD² − AD x AK; that is, as AD to
AD − AK or AC to CK: and therefore the particle TDV of the sector is
PDQ x AC
CK; and therefore (because AC and AD
are given) as PQ
CK; that is, as the increment of the
velocity directly, and as the force generating the increment
inversely; and therefore as the particle of the time answering to the
increment. And, by composition, the sum of the particles of time, in
which all the particles PQ of the velocity AP are generated, will be
as the sum of the particles of the sector ATD; that is, the whole time
will be as the whole sector. Q.E.D.

Cor. 1. Hence if AB be equal to a fourth part of AC, the space which a body will describe by falling in any time will be to the space which the body could describe, by moving uniformly on in the same time with its greatest velocity AC, as the area ABNK, which expresses the space described in falling to the area ATD, which expresses the time. For since AC is to AP as AP to AK, then (by Cor. 1, Lem. II, of this Book) LK is to PQ as 2AK to AP, that is, as 2AP to AC, and thence LK is to ½PQ as AP to ¼AG or AB; and KN is to AC or AD as AB to CK; and therefore, ex aequo, LKNO to DPQ as AP to CK. But DPQ was to DTV as CK to AC. Therefore, ex aequo, LKNO is to DTV as AP to AC; that is, as the velocity of the falling body to the greatest velocity which the body by falling can acquire. Since, therefore, the moments LKNO and DTV of the areas ABNK and ATD are as the velocities, all the parts of those areas generated in the same time will be as the spaces described in the same time; and therefore the whole areas ABNK and ADT, generated from the beginning, will be as the whole spaces described from the beginning of the descent. Q.E.D.
Cor. 2. The same is true also of the space described in the ascent. That is to say, that all that space is to the space described in the same time, with the uniform velocity AC, as the area ABuk is to the sector ADt.
Cor. 3. The velocity of the body, falling in the time ATD, is to the velocity which it would acquire in the same time in a non-resisting space, as the triangle APD to the hyperbolic sector ATD. For the velocity in a non-resisting medium would be as the time ATD, and in a resisting medium is as AP, that is, as the triangle APD. And those velocities, at the beginning of the descent, are equal among themselves, as well as those areas ATD, APD.
Cor. 4. By the same argument, the velocity in the ascent is to the velocity with which the body in the same time, in a non-resisting space, would lose all its motion of ascent, as the triangle ApD to the circular sector AtD; or as the right line Ap to the arc At.
Cor. 5. Therefore the time in which a body, by falling in a resisting medium, would acquire the velocity AP, is to the time in which it would acquire its greatest velocity AC, by falling in a non-resisting space, as the sector ADT to the triangle ADC: and the time in which it would lose its velocity Ap, by ascending in a resisting medium, is to the time in which it would lose the same velocity by ascending in a non-resisting space, as the arc At if to its tangent Ap.
Cor. 6. Hence from the given time there is given the space described in the ascent or descent. For the greatest velocity of a body descending in infinitum is given (by Corol. 2 and 3, Theor. VI, of this Book); and thence the time is given in which a body would acquire that velocity by falling in a non-resisting space. And taking the sector ADT or ADt to the triangle ADC in the ratio of the given time to the time just now found, there will be given both the velocity AP or Ap, and the area ABNK or ABnk, which is to the sector ADT, or ADt, as the space sought to the space which would, in the given time, be uniformly described with that greatest velocity found just before.
Cor. 7. And by going backward, from the given space of ascent or descent ABnk or ABNK, there will be given the time ADt or ADT.
Proposition x. Problem iii.
Suppose the uniform force of gravity to tend directly to the plane of the horizon, and the resistance to be as the density of the medium and the square of the velocity conjunctly: it is proposed to find the density of the medium in each place, which shall make the body move in any given curve line; the velocity of the body and the resistance of the medium in each place.
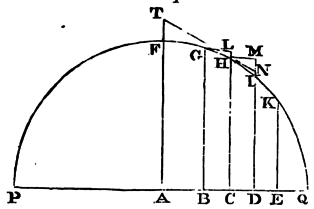
Let PQ, be a plane perpendicular to the plane of the scheme itself;
PFHQ a curve line meeting that plane in the points P and Q; G, H, I, K
four places of the body going on in this curve from F to Q; and GB,
HC, ID, KE four parallel ordinates let fall from these points to the
horizon, and standing on the horizontal line PQ, at the points B, C,
D, E; and let the distances BC, CD, DE, of the ordinates be equal
among themselves. From the points G and H let the right lines GL, HN,
be drawn touching the curve in G and H, and meeting the ordinates CH,
DI, produced upwards, in L and N: and complete the parallelogram HCDM.
And the times in which the body describes the arcs GH, HI, will be in
a subduplicate ratio of the altitudes LH, NI, which the bodies would
describe in those times, by falling from the tangents; and the
velocities will be as the lengths described GH, HI directly, and the
times inversely. Let the times be expounded by T and t, and
the velocities by GH
T and HI
t; and the decrement of the velocity
produced in the time t will be expounded by
GH
T − HI
t . This decrement arises from
the resistance which retards the body, and from the gravity which
accelerates it. Gravity, in a falling body, which in its fall
describes the space NI, produces a velocity with which it would be
able to describe twice that space in the same time, as Galileo
has demonstrated; that is, the velocity 2NI
t : but if the body describes the arc
HI, it augments that arc only by the length HI − HN or
MI x NI
HI; and therefore generates only the
velocity 2MI x NI
t x HI. Let this velocity be added to
the beforementioned decrement, and we shall have the decrement of the
velocity arising from the resistance alone, that is,
GH
T − HI
t + 2MI
x NI
t x HI . Therefore
since, in the same time, the action of gravity generates, in a falling
body, the velocity 2NI
t, the resistance will be to the
gravity as GH
T − HI
t + 2MI
x NI
t x HI or as
t x GH
T − HI + 2MI
x NI
HI to 2NI.

Now for the abscissas CB, CD, CE, put −o, o, 2o. For the
ordinate CH put P; and for MI put any series Qo + Ro²
+ So³ +, &c. And all the terms of the series after the
first, that is, Ro² + So³ +, &c., will be NI;
and the ordinates DI, EK, and BG will be P − Qo − Ro²
− So³ −, &c., P − 2Qo − 4Ro² − 8So³ −,
&c., and P + Qo − Ro² + So³ −, &c.,
respectively. And by squaring the differences of the ordinates BG − CH
and CH − DI, and to the squares thence produced adding the squares of
BC and CD themselves, you will have oo + QQoo − 2QRo³
+, &c., and oo + QQoo + 2QRo³ +,
&c., the squares of the arcs GH, HI; whose roots o√(1+QQ)
− QRoo
√(1+QQ) , and o√(1+QQ)
+ QRoo
√(1+QQ) are the arcs GH and
HI. Moreover, if from the ordinate CH there be subducted half the sum
of the ordinates BG and DI, and from the ordinate DI there be
subducted half the sum of the ordinates CH and EK, there will remain Roo
and Roo + 3So³, the versed sines of the arcs GI and
HK. And these are proportional to the lineolae LH and NI, and
therefore in the duplicate ratio of the infinitely small times T and t:
and thence the ratio t
T is √(
R + 3So
R) or
R + 3/2So
R ; and t
x GH
T − HI + 2MI
x NI
HI , by substituting the
values of t
T, GH, HI, MI and NI just found,
becomes 3Soo
2R √(1+QQ). And since 2NI is
2Roo, the resistance will be now to the gravity as
3Soo
2R √(1+QQ), that is, as
3S√(1+qq) to 4RR.
And the velocity will be such, that a body going off therewith from
any place H, in the direction of the tangent HN, would describe, in
vacuo, a parabola, whose diameter is HC, and its latus rectum
HN2
NI or 1+QQ
R.
And the resistance is as the density of the medium and the square of
the velocity conjunctly; and therefore the density of the medium is as
the resistance directly, and the square of the velocity inversely;
that is, as 3S√(1+QQ)
4RR directly and
1+QQ
R inversely; that is, as
S
R√(1+QQ). Q.E.I.
Cor. 1. If the tangent HN be produced both
ways, so as to meet any ordinate AF in T HT
AC will be equal to √(1+QQ);
and therefore in what has gone before may be put for √(1+QQ).
By this means the resistance will be to the gravity as 3S x HT to 4RR
x AC; the velocity will be as HT
AC√R, and the density of the medium
will be as S x AC
R x HT.
Cor. 2. And hence, if the curve line PFHQ be defined by the relation between the base or abscissa AC and the ordinate CH, as is usual, and the value of the ordinate be resolved into a converging series, the Problem will be expeditiously solved by the first terms of the series; as in the following examples.
Example 1. Let the line PFHQ be a semi-circle described upon the diameter PQ, to find the density of the medium that shall make a projectile move in that line.
Bisect the diameter PQ in A; and call AQ, n; AC, a;
CH, e; and CD, o; then DI² or AQ² − AD² = nn
− aa − 2ao − oo, or ee − 2ao − oo; and the root being
extracted by our method, will give DI = e −
ao
e − oo
2e − aaoo
2e3 −
ao3
2e3 −
a3o3
2e5 − , &c.
Here put nn for ee + aa, and DI will become
= e − ao
e − nnoo
2e3 −
anno3
2e5 −, &c
Such series I distinguish into successive terms after this manner: I
call that the first term in which the infinitely small quantity o
is not found; the second, in which that quantity is of one dimension
only; the third, in which it arises to two dimensions; the fourth, in
which it is of three; and so ad infinitum. And the first
term, which here is e, will always denote the length of the
ordinate CH, standing at the beginning of the indefinite quantity o.
The second term, which here is ao
e, will denote the difference between
CH and DN; that is, the lineola MN which is cut off by completing the
parallelogram HCDM; and therefore always determines the position of
the tangent HN; as, in this case, by taking MN to HM as
ao
e to o, or a to e.
The third term, which here is nnoo
2e3, will represent the
lineola IN, which lies between the tangent and the curve; and
therefore determines the angle of contact IHN, or the curvature which
the curve line
 has in H. If that lineola IN is of a finite magnitude, it will be expressed by
the third term, together with those that follow in infinitum.
But if that lineola be diminished in infinitum, the terms
following become in finitely less than the third term, and therefore
may be neglected. The fourth term determines the variation of the
curvature; the fifth, the variation of the variation; and so on.
Whence, by the way, appears no contemptible use of these series in the
solution of problems that depend upon tangents, and the curvature of
curves.
has in H. If that lineola IN is of a finite magnitude, it will be expressed by
the third term, together with those that follow in infinitum.
But if that lineola be diminished in infinitum, the terms
following become in finitely less than the third term, and therefore
may be neglected. The fourth term determines the variation of the
curvature; the fifth, the variation of the variation; and so on.
Whence, by the way, appears no contemptible use of these series in the
solution of problems that depend upon tangents, and the curvature of
curves.
Now compare the series e −
ao
e − nnoo
2e3 −
anno3
2e5 − &c., with
the series P − Qo − Roo − So³
− &c., and for P, Q, R and S, put e,
a
e, nn
2e3 and
ann
2e5, and for √(1
+ QQ) put √(1 +
aa
ee ) or
n
e : and the density of the medium will
come out as a
ne; that is (because n is
given), as a
e or AC
CH, that is, as that length of the
tangent HT, which is terminated at the semi-diameter AF standing
perpendicularly on PQ: and the resistance will be to the gravity as 3a
to 2n, that is, as 3AC to the diameter PQ of the circle; and
the velocity will be as √(CH). Therefore if
the body goes from the place F, with a due velocity, in the direction
of a line parallel to PQ, and the density of the medium in each of the
places H is as the length of the tangent HT, and the resistance also
in any place H is to the force of gravity as 3AC to PQ, that body will
describe the quadrant FHQ of a circle. Q.E.I.
But if the same body should go from the place P, in the direction of
a line perpendicular to PQ, and should begin to move in an arc of the
semi circle PFQ, we must take AC or a on the contrary side
of the centre A; and therefore its sign must be changed, and we must
put −a for +a. Then the density of the medium would
come out as −a
e. But nature does not admit of a
negative density, that is, a density which accelerates the motion of
bodies; and therefore it cannot naturally come to pass that a body by
ascending from P should describe the quadrant PF of a circle. To
produce such an effect, a body ought to be accelerated by an impelling
medium, and not impeded by a resisting one.
Example 2. Let the line PFQ be a parabola, having its axis AF perpendicular to the horizon PQ, to find the density of the medium, which will make a projectile move in that line.
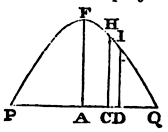
From the nature of the parabola, the rectangle PDQ is equal to the
rectangle under the ordinate DI and some given right line; that is, if
that right line be called b; PC, a; PQ, c;
CH, e; and CD, o; the rectangle a + o
into c − a − o or ac − aa − 2ao + co − oo, is
equal to the rectangle b into DI, and therefore DI is equal
to ac − aa
b + c
− 2a
bo − oo
b . Now the second term
c−2a
bo of this series is to be put
for Qo, and the third term oo
b for Roo. But since there are
no more terms, the co-efficient S of the fourth term will vanish; and
therefore the quantity S
R√(1+QQ), to which the density of the
medium is proportional, will be nothing. Therefore, where the medium
is of no density, the projectile will move in a parabola; as Galileo
hath heretofore demonstrated. Q.E.I.
Example 3. Let the line AGK be an hyperbola, having its asymptote NX perpendicular to the horizontal plane AK, to find the density of the medium that will make a projectile move in that line.
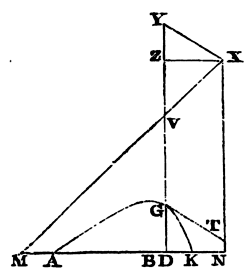
Let MX be the other asymptote, meeting the ordinate DG produced in V;
and from the nature of the hyperbola, the rectangle of XV into VG will
be given. There is also given the ratio of DN to VX, and therefore the
rectangle of DN into VG is given. Let that be bb: and,
completing the parallelogram DNXZ, let BN be called a; BD, o;
NX, c; and let the given ratio of VZ to ZX or DN be
m
n. Then DN will be equal to a − o,
VG equal to bb
a − o, VZ equal to
m
n x (a − o), and GD or
NX − VZ − VG equal to c −
m
n a + m
no − bb
a−o . Let the term
bb
a−o be resolved into the converging
series bb
a + bb
aao + bb
a3oo +
bb
a4o3 ,
&c., and GD will become equal to c −
m
na − bb
a + m
no − bb
aao − bb
a3o2 −
bb
a4o3 ,
&c. The second term
m
no − bb
aao of this series is to be
used for Qo; the third
bb
a3o2 ,
with its sign changed for Ro²; and the fourth
bb
a4o3 ,
with its sign changed also for So³, and their coefficients
m
n − bb
aa ,
bb
a3 and
bb
a4 are to be put for Q, R,
and S in the former rule. Which being done, the density of the medium
will come out as bb
a4
bb
a3 √(1 +
mm
nn − 2mbb
naa + b4
a4) or
1
√(aa + mm
nnaa − 2mbb
n + b4
aa) , that is, if in
VZ you take VY equal to VG, as 1
XY. For aa and
m2
n2a2 −
2mbb
n + b4
aa are the squares of XZ and
ZY. But the ratio of the resistance to gravity is found to be that of
3XY to 2YG; and the velocity is that with which the body would
describe a parabola, whose vertex is G, diameter DG, latus rectum
XY2
VG. Suppose, therefore, that the
densities of the medium in each of the places G are reciprocally as
the distances XY, and that the resistance in any place G is to the
gravity as 3XY to 2YG; and a body let go from the place A, with a due
velocity, will describe that hyperbola AGK. Q.E.I.
Example 4. Suppose, indefinitely, the line
AGK to be an hyperbola described with the centre
 X, and the asymptotes MX, NX, so that, having constructed the
rectangle XZDN, whose side ZD cuts the hyperbola in G and its
asymptote in V, VG may be reciprocally as any power DNn of
the line ZX or DN, whose index is the number n: to find the
density of the medium in which a projected body will describe this
curve.
X, and the asymptotes MX, NX, so that, having constructed the
rectangle XZDN, whose side ZD cuts the hyperbola in G and its
asymptote in V, VG may be reciprocally as any power DNn of
the line ZX or DN, whose index is the number n: to find the
density of the medium in which a projected body will describe this
curve.
For BN, BD, NX, put A, O, C, respectively, and let VZ be to XZ or DN
as d to e, and VG be equal to
bb
DNn; then DN will be equal
to A − O, VG = bb
(A − O)n ,
VZ = d
e (A − O), and GD or NX − VZ −
VG equal to
eA + d
eO − bb
(A − O)n .
Let the term bb
(A − O)n be resolved into
an infinite series
An + nbb
An + 1 x O + nn + n
2An + 2 x bb O2 + n3 + 3nn + 2n
6An + 3 x bb O3,&c.,
And GD will be equal to
eA + bb
An + d
e O − nbb
An + 1 O − + nn + n
2An + 2bb O2 − + n3 + 3nn + 2n
6An + 3 bbO3, &c.
The second term d
e O − nbb
An+1 O of this
series is to be used for Qo, the third
nn+n
2An+2bb O2
for Roo, the fourth
n3+3nn+2n
6An+3bbO3
for So³. And thence the density of the medium
S
R√(1+QQ), in any place G, will be
3√(A2 + dd
eeA2− 2dnbb
eAnA+ nnb4
A2n ),
and therefore if in VZ you take VY equal to n x VG, that
density is reciprocally as XY. For A² and
dd
eeA2 −
2dnbb
eAnA +
nnb4
A2n are the squares
of XZ and ZY. But the resistance in the same place G is to the force
of gravity as 3S x XY
A to 4RR, that is, as XY to
2nn + 2n
n + 2 VG. And the velocity there is the
same wherewith the projected body would move in a parabola, whose
vertex is G, diameter GD, and latus rectum 1
+ QQ
R or 2XY2
(nn + n) x VG. Q.E.I.
Scholium.

In the same manner that the density of the medium comes out to be as
S x AC
R x HT, in Cor. 1, if the resistance is
put as any power Vn of the velocity V, the density of the
medium will come out to be as
S
R4−n/2
x ( AC
HT)n−1
And therefore if a curve can be found, such that the ratio of
S
R4−n/2
to (
HT
AC )n−1, or of
S2
R4−n to (1+QQ)n−1
may be given; the body, in an uniform medium, whose resistance is as
the power Vn of the velocity V, will move in this curve.
But let us return to more simple curves.
Because there can be no motion in a parabola except in a
non-resisting medium, but in the hyperbolas here described it is
produced by a perpetual resistance; it is evident that the line which
a projectile describes in an uniformly
 resisting medium approaches nearer to these hyperbolas than to a
parabola. That line is certainly of the hyperbolic kind, but about the
vertex it is more distant from the asymptotes, and in the parts remote
from the vertex draws nearer to them than these hyperbolas here
described. The difference, however, is not so great between the one
and the other but that these latter may be commodiously enough used in
practice instead of the former. And perhaps these may prove more
useful than an hyperbola that is more accurate, and at the same time
more compounded. They may be made use of, then, in this manner.
resisting medium approaches nearer to these hyperbolas than to a
parabola. That line is certainly of the hyperbolic kind, but about the
vertex it is more distant from the asymptotes, and in the parts remote
from the vertex draws nearer to them than these hyperbolas here
described. The difference, however, is not so great between the one
and the other but that these latter may be commodiously enough used in
practice instead of the former. And perhaps these may prove more
useful than an hyperbola that is more accurate, and at the same time
more compounded. They may be made use of, then, in this manner.
Complete the parallelogram XYGT, and the right line GT will touch the
hyperbola in G, and therefore the density of the medium in G is
reciprocally as the tangent GT, and the velocity there as √
(GT2
GV); and the resistance is to
the force of gravity as GT to
2nn + 2n
n + 2 x GV.
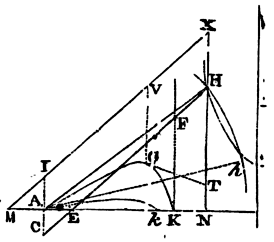
Therefore if a body projected from the place A, in the direction of
the right line AH, describes the hyperbola AGK and AH produced meets
the asymptote NX in H, and AI drawn parallel to it meets the other
asymptote MX in I; the density of the medium in A will be reciprocally
as AH, and the velocity of the body as √(
AH2
AI), and the resistance there
to the force of gravity as AH to
2nn + 2n
n + 2 x AI. Hence the
following rules are deduced.
Rule 1. If the density of the medium at A, and the velocity with which the body is projected remain the same, and the angle NAH be changed, the lengths AH, AI, HX will remain. Therefore if those lengths, in any one case, are found, the hyperbola may afterwards be easily determined from any given angle NAH.
Rule 2. If the angle NAH, and the density of the medium at A, re main the same, and the velocity with which the body is projected be changed, the length AH will continue the same; and AI will be changed in a duplicate ratio of the velocity reciprocally.
Rule 3. If the angle NAH, the velocity of the
body at A, and the accelerative gravity remain the same, and the
proportion of the resistance at A to the motive gravity be augmented
in any ratio; the proportion of AH to AI will be augmented in the same
ratio, the latus rectum of the abovementioned parabola remaining the
same, and also the length AH2
AI proportional to it; and therefore AH
will be diminished in the same ratio, and AI will be diminished in the
duplicate of that ratio. But the proportion of the resistance to the
weight is augmented, when either the specific gravity is made less,
the magnitude remaining equal, or when the density of the medium is
made greater, or when, by diminishing the magnitude, the resistance
becomes diminished in a less ratio than the weight.
Rule 4. Because the density of the medium is greater near the vertex of the hyperbola than it is in the place A, that a mean density may be preserved, the ratio of the least of the tangents GT to the tangent AH ought to be found, and the density in A augmented in a ratio a little greater than that of half the sum of those tangents to the least of the tangents GT.
Rule 5. If the lengths AH, AI are given, and the figure AGK is to be described, produce HN to X, so that HX may be to AI as n + 1 to 1; and with the centre X, and the asymptotes MX, NX, describe an hyperbola through the point A, such that AI may be to any of the lines VG as XVn to XIn.
Rule 6. By how much the greater the number n is, so much the more accurate are these hyperbolas in the ascent of the body from A, and less accurate in its descent to K; and the contrary. The conic hyperbola keeps a mean ratio between these, and is more simple than the rest. Therefore if the hyperbola be of this kind, and you are to find the point K, where the projected body falls upon any right line AN passing through the point A, let AN produced meet the asymptotes MX, NX in M and N, and take NK equal to AM.
Rule 7. And hence appears an expeditious
method of determining this hyperbola from the phenomena. Let two
similar and equal bodies be projected with the same velocity, in
different angles HAK, hAk, and let them fall upon
the plane of the horizon in K and k; and note the proportion
of AK to Ak. Let it be as d to e. Then
erecting a perpendicular AI of any length, assume any how the length
AH or Ah, and thence graphically, or
by scale and compass, collect the lengths AK, Ak (by Rule 6).
If the ratio of AK to Ak be the same with that of d
to e, the length of AH was
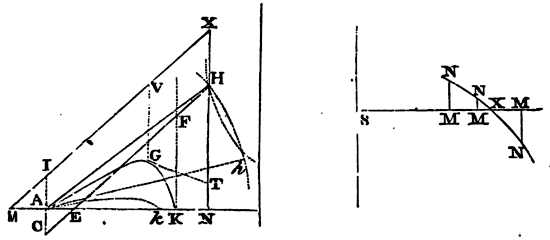 rightly assumed. If not, take on the indefinite right line SM, the
length SM equal to the assumed AH; and erect a perpendicular MN equal
to the difference AK
rightly assumed. If not, take on the indefinite right line SM, the
length SM equal to the assumed AH; and erect a perpendicular MN equal
to the difference AK
Ak − d
e of the ratios drawn into any
given right line. By the like method, from several assumed lengths AH,
you may find several points N; and draw through them all a regular
curve NNXN, cutting the right line SMMM in X. Lastly, assume AH equal
to the abscissa SX, and thence find again the length AK; and the
lengths, which are to the assumed length AI, and this last AH, as the
length AK known by experiment, to the length AK last found, will be
the true lengths AI and AH, which were to be found. But these being
given, there will be given also the resisting force of the medium in
the place A, it being to the force of gravity as AH to 4/3AI.
Let the density of the medium be increased by Rule 4, and if the
resisting force just found be increased in the same ratio, it will
become still more accurate.
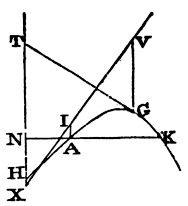
Rule 8. The lengths AH, HX being found; let
there be now required the position of the line AH, according to which
a projectile thrown with that given velocity shall fall upon any point
K. At the joints A and K, erect the lines AC, KF perpendicular to the
horizon; whereof let AC be drawn downwards, and be equal to AI or ½HX.
With the asymptotes AK, KF, describe an hyperbola, whose conjugate
shall pass through the point C; and from the centre A, with the
interval AH, describe a circle cutting that hyperbola in the point H;
then the projectile thrown in the direction of the right line AH will
fall upon the point K. Q.E.I. For the point H,
because of the given length AH, must be somewhere in the circumference
of the described circle. Draw CH meeting AK and KF in E and F; and
because CH, MX are parallel, and AC, AI equal, AE will be equal to AM,
and therefore also equal to KN. But CE is to AE as FH to KN, and
therefore CE and FH are equal. Therefore the point H falls upon the
hyperbolic curve described with the asymptotes AK, KF whose conjugate
passes through the point C; and is therefore found in the
 common intersection of this hyperbolic curve
and the circumference of the described circle. Q.E.D. It
is to be observed that this operation is the same, whether the right
line AKN be parallel to the horizon, or inclined thereto in any angle;
and that from two intersections H, h, there arise two angles
NAH, NAh; and that in mechanical practice it is sufficient
once to describe a circle, then to apply a ruler CH, of an
indeterminate length, so to the point C, that its part FH, intercepted
between the circle and the right line FK, may be equal to its part CE
placed between the point C and the right line AK
common intersection of this hyperbolic curve
and the circumference of the described circle. Q.E.D. It
is to be observed that this operation is the same, whether the right
line AKN be parallel to the horizon, or inclined thereto in any angle;
and that from two intersections H, h, there arise two angles
NAH, NAh; and that in mechanical practice it is sufficient
once to describe a circle, then to apply a ruler CH, of an
indeterminate length, so to the point C, that its part FH, intercepted
between the circle and the right line FK, may be equal to its part CE
placed between the point C and the right line AK
What has been said of hyperbolas may be easily applied to parabolas.
For if a parabola be represented by XAGK, touched by a right line XV
in the vertex X, and the ordinates IA, VG be as any powers XIn,
XVn, of the abscissas XI, XV; draw XT, GT, AH, whereof let
XT be parallel to VG, and let GT, AH touch the parabola in G and A:
and a body projected from any place A, in the direction of the right
line AH, with a due velocity, will describe this parabola, if the
density of the medium in each of the places G be reciprocally as the
tangent GT. In that case the velocity in G will be the same as would
cause a body, moving in a nonresisting space, to describe a conic
parabola, having G for its vertex, VG produced downwards for its
diameter, and 2GT2
(nn − n) x VG for its latus
rectum. And the resisting force in G will be to the force of gravity
as GT to 2nn −
2n
n − 2VG. Therefore if NAK
represent an horizontal line, and both the density of the medium at A,
and the velocity with which the body is projected, remaining the same,
the angle NAH be any how altered, the lengths AH, AI, HX will remain;
and thence will be given the vertex X of the parabola, and the
position of the right line XI; and by taking VG to IA as XVn
to XIn, there will be given all the points G of the
parabola, through which the projectile will pass.